Эвольвентное зацепление

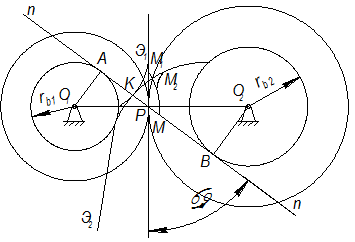
Рис. 1.29

Пусть профиль зуба звена 1 (Рис. 1.29) очерчен по эвольвенте 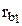, a профиль зуба звена 2 по эвольвенте 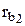. Поместим центры этих окружностей в точку 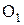и точку 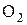и приведём эвольвенты в соприкосновение в точке К.

Нормаль к эвольвенте 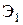в точке К должна быть касательной к 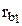, а нормаль 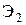- касательной к 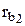. В точке касания нормаль должна быть общей к обоим профилям и, следовательно, точка К лежит на общей касательной к основным окружностям. При вращении звеньев 1 и 2 точка касания эвольвент перемещается по отрезку АВ этой касательной, так как вне отрезка АВ эвольвенты не могут касаться, то есть иметь общую нормаль. Отсюда следует, что линия зацепления эвольвентных профилей совпадает с общей нормалью к ним и лежит на отрезке АВ общей касательной к основным окружностям. 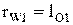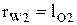Точка Р – полюс зацепления занимает неизменное положение, следовательно центры в относительном движении представляют собой окружности с радиусами и соответственно. По свойству центроид начальные окружности при движении звеньев перекатываются без скольжения. Итак, при эвольвентном зацеплении передаточное отношение имеет постоянную величину

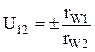
Знак (-) относится к внешнему зацеплению, знак (+) относится к внутреннему зацеплению.

Из треугольника 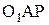и треугольника следует:

,

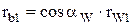
следовательно, 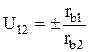отсюда можно сделать выводы:

1. При эвольвентном зацеплении изменение межосевого расстояния не влияет на величину передаточного отношения, вследствие неизменности радиусов основных окружностей. При изменении межосевого расстояния изменятся лишь радиусы 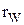и угловые зацепления .

2. При эвольвентном зацеплении передаточное отношение, согласно основной теории имеет постоянную величину.

3. При внешнем зацеплении эвольвентные профили являются сопряжёнными только в пределах отрезка АВ линии зацепления.

Линией зацепления (АВ) называется геометрическое место точек соприкасания профилей боковых поверхностей зубьев колес, принадлежащее неподвижному пространству. Точк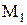и и 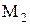- сопряженные.

Точки, касающиеся друг друга на линии зацепления, называются сопряжёнными.

Точки А и В - теоретические границы зацепления, за этими точками зацепление допускать нельзя - наступит заклинивание передачи.