Образование эвольвенты и её свойства

Эвольвентой круга называют кривую, которая описывает любую точку прямой, перекатывающейся без скольжения по окружности. При этом прямую обычно называют производящей, а окружность - основной .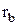

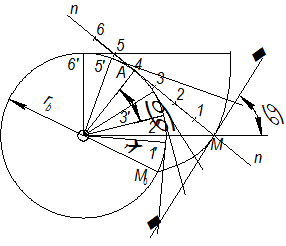
Пусть производящая прямая (рис. 1.27) n – n показана в положении, когда она касается основной окружности в точке А и требуется построить эвольвенту, описываемую т. М. Делим отрезок AM на равные части и откладываем на 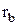дуги равные соответствующим частям отрезка AM: 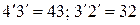и так далее. Через полученные точки проводим касательные и откладываем на них отрезки, последовательно уменьшая длину каждого отрезка на одну часть. Соединяя концы отложенных отрезков, получаем эвольвенту. Уравнение эвольвенты получим из условия перекатывания производящей прямой по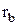

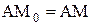
(2.13)

Рис. 1.27

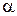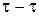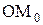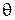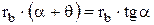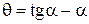Обозначим через острый угол между касательной к эвольвенте и радиус-вектором эвольвенты ОМ. Этот угол называется углом профиля. Угол, образованный начальным радиус-вектором эвольвенты и её текущим радиусом ОМ называется эвольвентным углом ( ). Тогда условие (1.14) принимает вид: или . Функция 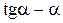называется инвалютой и обозначается "inv", то есть уравнение может быть записано 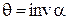. Радиус-вектор эвольвенты находится из треугольника ОАМ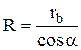

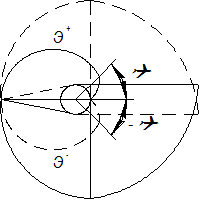
Эвольвента имеет две ветви (рис. 1.28): положительная ветвь 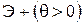получается при перекатывании прямой против хода часовой стрелки, отрицательная 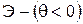- при перекатывании по ходу часовой стрелки.

Рис. 1.28