Основная теорема зацепления
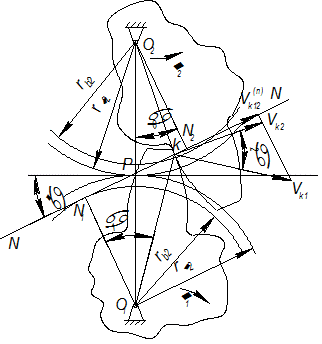
Основную теорему зацепления рассмотрим на примере двух зубчатых колес (рис. 26). Профили зубьев двух колёс, соприкасаются в точке К. Колёса вращаются вокруг точек 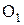 и
и 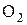 в направлениях указанных стрелками. Скорость точки К в системе первого колеса:
в направлениях указанных стрелками. Скорость точки К в системе первого колеса:
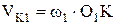
| (1.9) |
Скорость точки К в системе второго колеса:
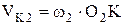
| (1.10) |
Они различны по величине и направлению.
Давление между двумя твёрдыми телами передаётся по общее нормали N-N, следовательно, непрерывная передача движения возможна только лишь в том случае, если проекции скоростей точек контакта обоих профилей на общую нормаль будут одинаковы по величине и направлению.
При 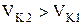 будет происходить размыкание зацепления, чего допускать нельзя; при
будет происходить размыкание зацепления, чего допускать нельзя; при 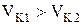 - происходит внедрение зуба одного колеса в зуб другого колеса другой (тем более нельзя допускать), следовательно, скорости должны быть равны
- происходит внедрение зуба одного колеса в зуб другого колеса другой (тем более нельзя допускать), следовательно, скорости должны быть равны 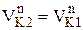
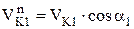
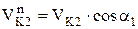 ,
,
так как 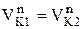 ,
,
то 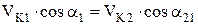
или учитывая (1.9) и (1.10) получим:
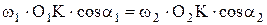
| (1.11) |
Из точек 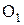 и
и 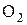 опустим перпендикуляры
опустим перпендикуляры 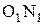 и
и 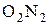 на общую нормаль N-N
на общую нормаль N-N
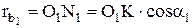 ;
;
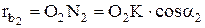
|
| Рис. 1.26 |
следовательно, подставив в формулу (1.11) получим: 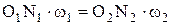
откуда
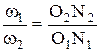
| (1.12) |
Соединим центры вращения профилей линей 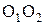 ; и точку пересечения с общей нормалью N-N обозначим Р.
; и точку пересечения с общей нормалью N-N обозначим Р.
Из подобия треугольников 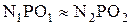 следует:
следует: 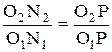 , учитывая формулу (1.12) получим:
, учитывая формулу (1.12) получим:
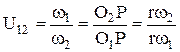
| (1.13) |
Это равенство выражает основную теорему зацепления: общая нормаль N-N к сопряжённым профилям, вращающимся относительно центров 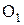 и
и 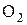 , делит линию центров
, делит линию центров 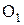 и
и 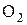 на части обратно пропорциональные угловым скоростям этих профилей.
на части обратно пропорциональные угловым скоростям этих профилей.
Итак: если точка Р неподвижна, то передаточное отношение звеньев будет постоянно. Точка Р называется полюсом зацепления. Она является мгновенным центром относительного вращения звеньев 1 и 2. Окружности с центрами 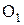 и
и 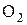 проходящие через полюс называются начальными. При работе колёс катятся одна по другой без скольжения. Следовательно, как вытекает из формулы (1.13), они представляют собой центроиды колёс.
проходящие через полюс называются начальными. При работе колёс катятся одна по другой без скольжения. Следовательно, как вытекает из формулы (1.13), они представляют собой центроиды колёс.
Угол 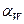 , составленный общей нормалью N–N к профилям зубьев (линией зацепления) и общей касательной к начальным окружностям называется углом зацепления (углом давления).
, составленный общей нормалью N–N к профилям зубьев (линией зацепления) и общей касательной к начальным окружностям называется углом зацепления (углом давления).
По теореме зацепления всегда можно проверить, являются ли два профиля находящихся в зацеплении зубьев сопряженными. Для этого проводим к ним общую нормаль и выясняем, проходит ли она через полюс зацепления. Требование сопряжённости профилей удовлетворяется, если профили являются эвольвентными, циклоидными и в некоторых других случаях. В эвольвентном зацеплении угол 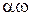 постоянный. В большинстве случаев угол
постоянный. В большинстве случаев угол 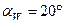 .
.
Дата добавления: 2021-12-14; просмотров: 482;











