Нулевые, положительные и отрицательные зубчатые колёса и передачи
Возможны три варианта расположения средней линии инструментальной рейки относительно делительной окружности колеса.
1. Средняя прямая производительного контура С-С касается делительной окружности заготовки (рис. 35 б). Средняя линия катится без скольжения по делительной окружности равной ширине впадине рейки по средней линии. 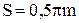 . Это колесо называется колесом с равноделенным шагом.
. Это колесо называется колесом с равноделенным шагом.
|
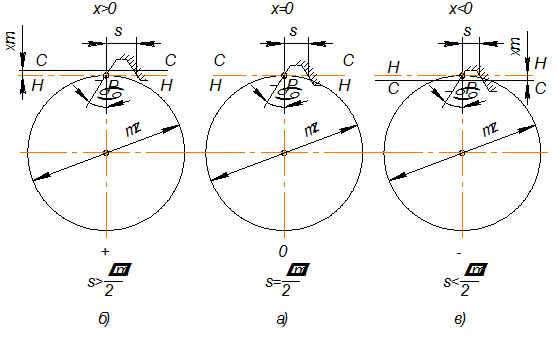
| Рис. 1.35 |
2. Средняя линия С-С смещена (поднята) на величину 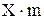 , где Х - коэффициент смещения (рис. 1.35 а). По делительной окружности катится без скольжения начальная окружность Н-Н, отстоящая от средней прямой линии на
, где Х - коэффициент смещения (рис. 1.35 а). По делительной окружности катится без скольжения начальная окружность Н-Н, отстоящая от средней прямой линии на 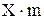 . Толщина зуба по делительной окружности оказывается больше ширины впадины, что соответствует увеличению ширины впадины производящего контура начальной прямой Н-Н. Из рисунков следует:
. Толщина зуба по делительной окружности оказывается больше ширины впадины, что соответствует увеличению ширины впадины производящего контура начальной прямой Н-Н. Из рисунков следует:
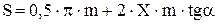
| (1.14) |
Коэффициент смещения Х в этом случае считается положительным.
3. Средняя прямая С-С смещена к центру на величину Хm, при чем коэффициент смещения Х считается отрицательным (рис. 1.35 в).
Толщина зуба по делительной окружности тоже определяется по формуле (1.14) и вследствие того, что 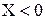 , оказывается меньше, чем у колеса с равноделенным шагом.
, оказывается меньше, чем у колеса с равноделенным шагом.
Зубчатые колеса, нарезанные со сдвигом рейки, называются исправленными колесами. Колеса, нарезанные с положительным сдвигом, называют положительными. А нарезанные с отрицательным сдвигом - отрицательными. Колеса, нарезаемые без сдвига, называют нулевыми колесами.
Для того чтобы, определить к какой из этих групп относится зубчатое колесо, надо определить толщину его зубьев по делительной окружности.
В зависимости от смещений каждого колеса можно получить три типа передач отличающихся расположением начальных и делительных окружностей.
I тип (рис. 1.36 а). Эти окружности совпадают, если передачи удовлетворяют условию 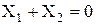 , передача называется нулевой,
, передача называется нулевой,
то есть, передачи, составленные из колес без смещения и передачи в которых отрицательное смещение одного колеса равно по абсолютной величине положительному смещению другого колеса (равносмещенные).
Межосевое расстояние в этих передачах 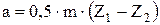 называется делительным межосевым расстоянием, а угол зацепления
называется делительным межосевым расстоянием, а угол зацепления  равен углу профиля производящего контура.
равен углу профиля производящего контура.
II тип (рис. 1.36 б). В передачах, у которых по делительным окружностям толщина зуба одного колеса больше ширины впадины другого, для зацепления без бокового зазора межцентровое расстояние 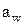 должно быть больше а.
должно быть больше а.
Соответственно увеличивается и угол 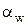 .
.
III тип (рис. 1.36 в). Аналогично для передач, у которых по делительной окружности толщина зубьев одного из колес меньше впадины другого, имеем 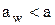 . Эти передачи получаются при
. Эти передачи получаются при 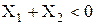
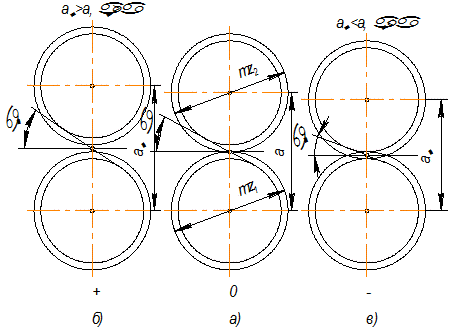
|
| Рис. 1.36 |
Геометрический расчет зубчатых передач при заданных смещениях X1 и X2
Для вычисления 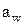 и
и 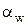 определяем сначала толщину зуба по начальной окружности.
определяем сначала толщину зуба по начальной окружности.
|
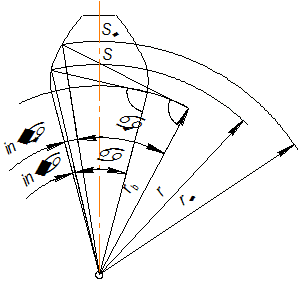
| Рис. 1.37 |
Из (рис. 1.37) с учетом уравнения эвольвенты 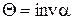 имеем:
имеем:
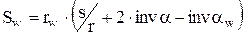
Подставив значение толщины зуба по делительной окружности:
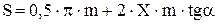
и учитывая
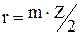 и
и 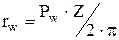 ,
,
где 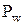 - шаг по начальной окружности получаем:
- шаг по начальной окружности получаем:
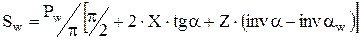
| (1.15) |
Для начальных окружностей сумма толщин зубьев равна шагу
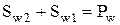
Отсюда с учетом формулы (1.15)
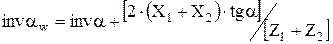
по таблице определяем 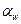 .
.
Радиусы начальных окружностей определим из 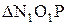
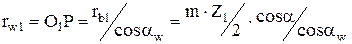
из 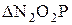
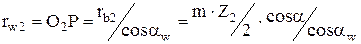
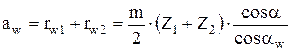 .
.
Радиусы впадин rf1 получаются из условия, что делительная головка режущего инструмента, равная по высоте 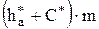 , при обработке проходит внутрь делительной окружности на величину
, при обработке проходит внутрь делительной окружности на величину 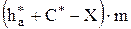 . Отсюда:
. Отсюда:
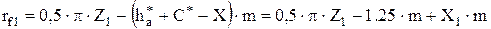 ,
,
где 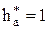 ,
,  ,
,
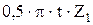 - делительная окружность,
- делительная окружность,
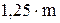 - высота ножки,
- высота ножки,
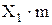 - смещение рейки.
- смещение рейки.
Радиусы вершин 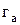 получаются из условия получения радиального зазора
получаются из условия получения радиального зазора 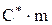 .
.
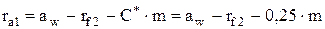
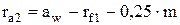
Дата добавления: 2021-12-14; просмотров: 547;











