Расчеты на прочность и жесткость при кручении.
Прочность бруса, работающего на кручение, считают обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном сечении, не превышают допускаемых:
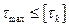
Конечно, незначительное (до 5...6%) превышение расчетного напряжения над допускаемым не опасно.
Эпюры касательных напряжений для круглого сплошного и кольцевого поперечных сечений показаны на рис. 19.16.
В точках, равноудаленных от центра сечения, напряжения одинаковы.
 Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения.
Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения.
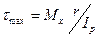
где 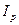 – полярный момент инерции.
– полярный момент инерции.
Введя обозначение 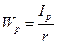 , получим следующее выражение для максимального касательного напряжения:
, получим следующее выражение для максимального касательного напряжения:
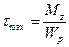 (19.12)
(19.12)
Величину 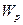 (мм3), равную отношению полярного момента инерции сечения к его радиусу, называют полярным моментом сопротивления сечения. Его размерность – L3. Очевидно, полярный момент сопротивления является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении.
(мм3), равную отношению полярного момента инерции сечения к его радиусу, называют полярным моментом сопротивления сечения. Его размерность – L3. Очевидно, полярный момент сопротивления является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении.
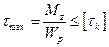 (19.13)
(19.13)
Эта формула служит для проверочного расчета на прочность.
При проектном расчете и при определении допускаемой нагрузки (момента) из формулы (19.13) соответственно находят 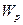 или
или 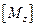
Для кольца:

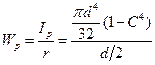 ;
;
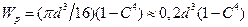 (19.14)
(19.14)
и для круга:
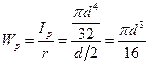
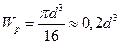 (19.15)
(19.15)
Для конструкционной углеродистой стали обычно 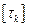 = 20..35 МПа.
= 20..35 МПа.
Во многих случаях вал должен быть рассчитан не только на прочность, но и на жесткость при кручении.
Рассмотрим брус, жестко защемленный одним концом и нагруженный на свободном конце скручивающим моментом М (рис. 19.17). При деформации
 бруса его поперечные сечения повернутся на некоторые углы по отношению к своему первоначальному положению или, что то же, по отношению к неподвижному сечению (заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки. Так, для произвольного сечения I, отстоящего от заделки на расстоянии Z ,он равен
бруса его поперечные сечения повернутся на некоторые углы по отношению к своему первоначальному положению или, что то же, по отношению к неподвижному сечению (заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки. Так, для произвольного сечения I, отстоящего от заделки на расстоянии Z ,он равен 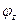 , для сечения II –
, для сечения II – 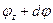 .Здесь
.Здесь 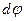 – угол поворота сечения II относительно I или угол закручивания элемента бруса длиной
– угол поворота сечения II относительно I или угол закручивания элемента бруса длиной 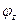 .
.
Вообще угол поворота произвольного сечения равен углу закручивания части бруса, заключенной между этим сечением и заделкой. Таким образом, угол поворота 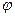 торцового сечения представляет собой полный угол закручивания рассматриваемого бруса.
торцового сечения представляет собой полный угол закручивания рассматриваемого бруса.
За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины) вала, обозначаемый 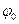 (встречается обозначение
(встречается обозначение 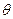 ).
).
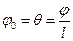 (19.16)
(19.16)
Угол закручивания бруса постоянного диаметра при одинаковом во всех поперечных сечениях крутящем моменте равен
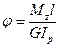 (19.17)
(19.17)
где l – длина рассматриваемого участка, мм.
В отличие от допускаемого напряжения, зависящего в первую очередь от материала вала, допускаемый угол закручивания зависит от назначения вала.
Значения допускаемых углов закручивания, встречающихся в различных отраслях машиностроения, весьма разнообразны; наиболее распространены значения 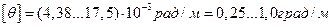
Условие жесткости при кручении имеет вид
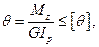 (19.18)
(19.18)
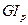 – условно жесткость сечения круглого бруса при кручении. Модуль сдвига (G) характеризует жесткость материала, а полярный момент инерции (
– условно жесткость сечения круглого бруса при кручении. Модуль сдвига (G) характеризует жесткость материала, а полярный момент инерции ( 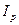 ) является геометрической характеристикой жесткости бруса.
) является геометрической характеристикой жесткости бруса. 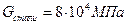
При проектном расчете отсюда определяют требуемое значение 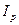 , а затем по формуле (19.19) или (19.20) вычисляют диаметр вала. Из двух значений диаметра вала, определенных из расчетов на прочность и жесткость, в качестве окончательного (исполнительного размера) должен быть, конечно, принят больший.
, а затем по формуле (19.19) или (19.20) вычисляют диаметр вала. Из двух значений диаметра вала, определенных из расчетов на прочность и жесткость, в качестве окончательного (исполнительного размера) должен быть, конечно, принят больший.
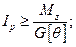 (19.19)
(19.19)
Для круга
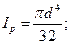
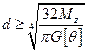 (19.20)
(19.20)
19.8. Условие прочности вала при совместном действии
крутящего и изгибающего моментов.
 При ориентировочном расчете валов влияние изгиба не учитывалось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенсировать ошибку, являющуюся следствием пренебрежения изгибом.
При ориентировочном расчете валов влияние изгиба не учитывалось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенсировать ошибку, являющуюся следствием пренебрежения изгибом.
Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения.
При расчете валов, а также других элементов конструкций, испытывающих одновременное действие изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответствующие им касательные напряжения в опасных точках бруса, невелики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба.
На рис.19.18 а показан вал, на который насажены зубчатое колесо диаметром 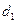 и шкив ременной передачи диаметром
и шкив ременной передачи диаметром 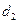 На зубчатое колесо действуют окружная
На зубчатое колесо действуют окружная 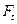 и радиальная
и радиальная 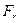 силы, на шкив – силы
силы, на шкив – силы 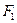 и
и 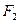
натяжения ветвей ремня. Для составления расчетной схемы вала (рис. 19.18 б) все силы должны быть приведены к его оси. При переносе силы 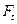 к оси вала добавляется скручивающая пара с моментом
к оси вала добавляется скручивающая пара с моментом 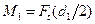 (рис. 19.19 а); аналогично, при приведении сил
(рис. 19.19 а); аналогично, при приведении сил 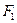 и
и 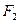 получается скручивающая пара с моментом
получается скручивающая пара с моментом

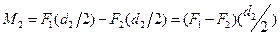 (рис. 19.19 б).
(рис. 19.19 б).
При равномерном вращении вала (только такой случай и рассматривается) 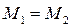 , что следует из основного уравнения динамики для вращательного движения.
, что следует из основного уравнения динамики для вращательного движения.
На основе расчетной схемы определяют опорные реакции и строят эпюры 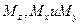 , по которым определяют опасное сечение вала.
, по которым определяют опасное сечение вала.
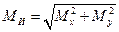 (19.21)
(19.21)
Для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий 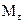 и изгибающий
и изгибающий 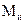 моменты. В рассматриваемом случае опасным будет сечение C под серединой шкива.
моменты. В рассматриваемом случае опасным будет сечение C под серединой шкива.
Валы, как правило, изготовляют из среднеуглеродистой конструкционной или реже легированной стали. Их расчет выполняют на основе третьей или пятой гипотез прочности.
Составим расчетную зависимость по третьей гипотезе прочности.
По формуле
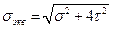 (19.22)
(19.22)
подставляя в нее значения 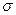 и
и 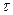 , получаем
, получаем
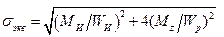 (19.23)
(19.23)
Учитывая, что для круглого (сплошного или кольцевого) сечения 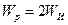 , имеем
, имеем
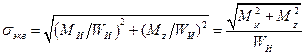 (19.24)
(19.24)
Внешне эта формула аналогична расчетной зависимости для определения максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным(или приведенным) моментом, при этом условие прочности имеет вид
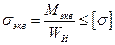 (19.25)
(19.25)
Расчет бруса круглого поперечного сечения на изгиб с кручением ведется аналогично расчету на изгиб, но вместо изгибающего момента в расчетную
формулу входит так называемый эквивалентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности. По гипотезе наибольших касательных напряжений,
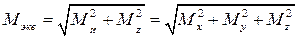 (19.26)
(19.26)
При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения:
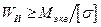 (19.27)
(19.27)
Учитывая, что для сплошного круглого сечения 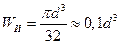 получаем следующую формулу для определения требуемого диаметра вала:
получаем следующую формулу для определения требуемого диаметра вала:
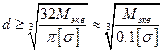 (19.28)
(19.28)
Понятие "эквивалентный момент" не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого сечения испытывает растяжение или сжатие.
Для бруса с постоянным диаметром опасная точка находится в сечении, для которого эквивалентный момент имеет наибольшее значение. Это сечение также называют опасным. Для отыскания опасного сечения иногда помимо эпюр 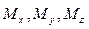 строят эпюру
строят эпюру 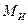 , а затем эпюру
, а затем эпюру 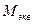 . Практически в этом нет необходимости; в случае, если по эпюрам
. Практически в этом нет необходимости; в случае, если по эпюрам 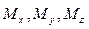 положение опасного сечения нельзя определить, проще вычислить
положение опасного сечения нельзя определить, проще вычислить 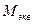 для нескольких сечений, чем строить эпюры
для нескольких сечений, чем строить эпюры 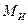 и
и 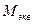 .
.
Дата добавления: 2021-12-14; просмотров: 765;











