Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия

Вместо построения силового многоугольника равнодействующую

системы сходящихся сил более точно и значительно быстрее находят вычислением с помощью метода проекций, который обычно называется аналитическим.

Проекцией вектора 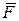на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущен­ными из начала и конца вектора 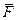. Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси;

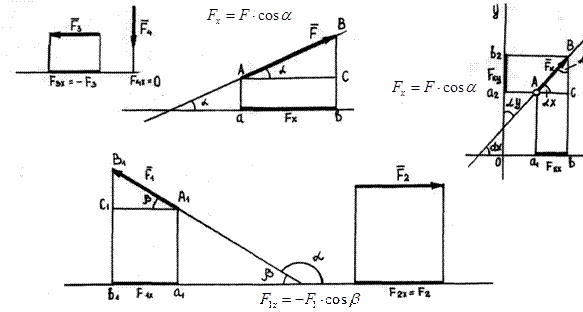
Рассмотрим теперь определение равнодействующей системы сходящихся сил методом проекций.

Допустим, что для заданной системы сходящихся сил построен многоугольник ABCDE, в котором вектор 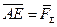– искомая равнодействующая данной системы.

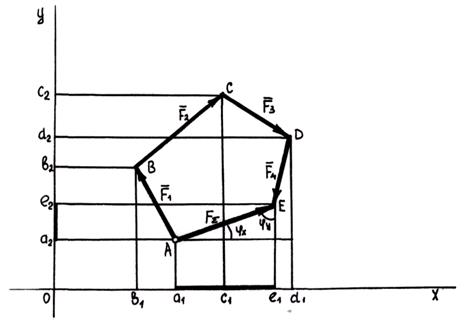
Выбрав систему координатных осей X и Y в плоскости силового многоугольника, спроецируем его на эти оси.

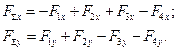
Эти равенства короче записываются так:

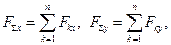
где 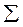– знак суммы, а индекс 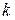принимает последовательно значения от 1 до n по числу сходящихся сил, равнодействующую которых определяем.

Таким образом, проекция равнодействующей системы сходящихся сил на каждую из осей координат равна алгебраической сумме проекций составляющих сил на ту же ось.

.

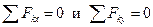В аналитической форме условие равновесия плоской системы сходящихся сил: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух осей координат были равны нулю.