Сложение плоской системы сходящихся сил. Геометрическое условие равновесия

Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке, называется плоской системой сходящихся сил. Если силы сходящейся системы приложены к разным точкам тела, то, по первому следствию из аксиом статики, каждую силу можно перенести в точку пересечения линий действия и по­лучить эквивалентную систему сил, приложенных к одной точке.

Две силы, приложенные к одной точке тела, образуют простей­шую плоскую систему сходящихся сил (две пересекающиеся прямые всегда лежат в одной плоскости).

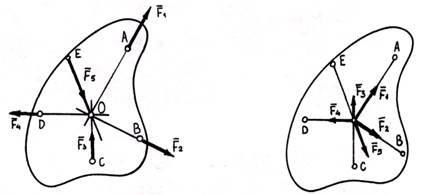
Рассмотрим систему сил 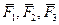, приложенных в точке А. Требуется найти их равнодействующую.

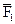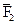Применив правило силового треугольника, сложим силы и . Для этого из конца вектора 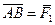отложим вектор 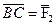и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил 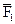и :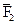

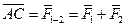
Теперь сложим силу 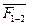с силой 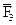. Для этого из конца вектора ВС= 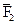отложим вектор 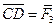и, соединив точки А и D, получим равнодействующую трех сил:

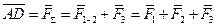
где – искомая равнодействующая

Порядок построения сторон силового многоугольника не влияет на окончательный результат.

Чтобы уравновесить систему сил, достаточно к ней добавить еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону.

В геометрической форме необходимое и достаточное условие равновесия системы сходящихся сил: система сходящихся сил уравновешена тогда и только тогда, когда силовой многоугольник замкнут.