Параллельное соединение сопротивлений.

При параллельном соединении сопротивлений суммируются проводимости. Например для преобразования схемы

(рис.1.6,б) используя первый закон Кирхгофа и закон Ома.

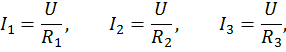
	(1.18)
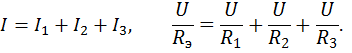
	(1.19)

Отсюда следует, что

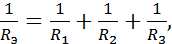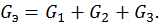
(1.20)

Таким образом, при параллельном соединении сопротивлений эквивалентная проводимость равна сумме проводимостей, откуда эквивалентное сопротивление имеет вид:

RЭ= .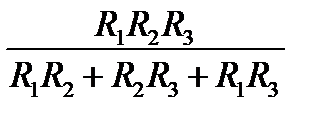

(1.21)

При параллельном соединении двух одинаковых сопротивлений R эквивалентное сопротивление будет R/2, трех сопротивлений – R/3 и т.д.‘

При смешанном соединении в цепи есть участки разных соединений.

2.6.2 Соединение звездой и треугольником.

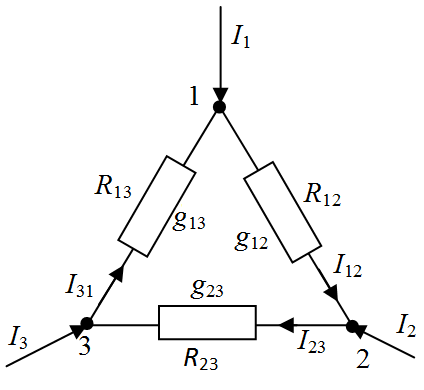
Из равенства сопротивлений в обеих схемах между двумя узлами при разомкнутом третьем легко выводятся выражения для преобразование звезда – треугольник (рис.1.7,а),

,

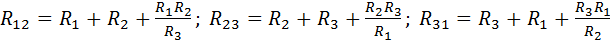а)	б)
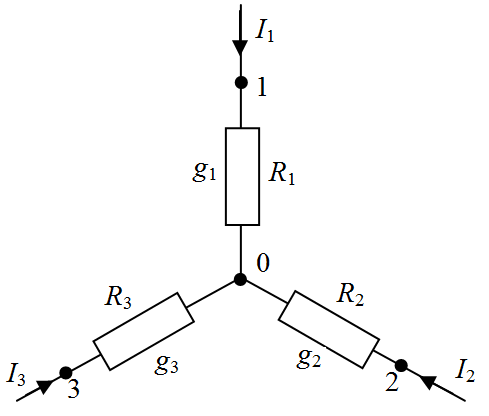
Рис. 1.7. Соединение сопротивлений при преобразовании равностороннего треугольника (а) в звезду (б)

для преобразование треугольник – звезда (рис.2.5,б)

.

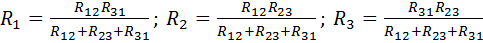При преобразовании равностороннего треугольника в звезду у последней сопротивления будут в три раза меньше и наоборот (рис.1.7,в).