Математический маятник

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием силы тяжести.

Момент инерции материальной точки относительно оси вращения проходящей через точку подвеса равен

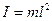
Математический маятник является частным случаем физического маятника, поэтому, период колебаний математического маятника можно вычислить по формуле (5.24), учитывая, что приведенная длина физического маятника и длина математического маятника равны (L = l)

.

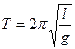Затухание колебания

Движение в реальных системах всегда сопровождается трением и в результате потери энергии колебания затухают. Свободные колебания всегда являются затухающими. Затухающие колебания можно продемонстрировать с помощью установки изображенной на рис.5.6. Если привести в колебание воронку с песком, то при ее движении всыпающийся песок оставляет след затухающих колебаний.

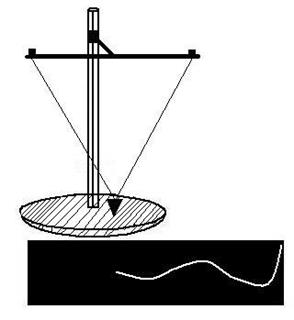
Рис.5.6

При малых скоростях колебания сила трения пропорциональна скорости

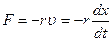(5.25)

где r – коэффициент сопротивления.

На колеблющуюся систему массой m действует сумма сил ( 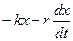), которая вызывает ускорение 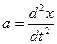этой системы, т.е.

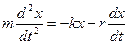
или

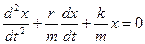(5.26)

Зная, что 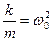и, обозначив 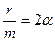(α – коэффициент затухания), получим дифференциальное уравнение затухающих колебаний

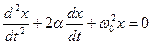(5.27)

Решением этого уравнения при условии ω₀ > α является выражение

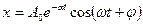(5.28)

Здесь 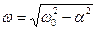– частота затухающих колебаний, а постоянные А₀ и φ зависят от начальных условий.

На рис.5.7. представлен график функции (5.28). На графике пунктиром показаны кривые затухания амплитуд. Уменьшение амплитуд происходит по закону

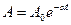(5.29)

где α – коэффициент затухания, характеризующий скорость затухания колебаний.

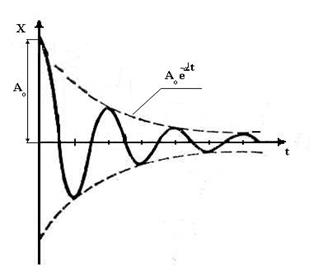
Рис.5.7

Найдем время τ, в течение которого амплитуда уменьшается в е раз. Если в формулу (5.29) подставить 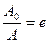, получим

at = 1 или .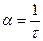

Следовательно, коэффициент затухания обратно пропорционален времени, за которое амплитуда уменьшается в е раз.

Мерой затухания является величина называемая логарифмическим декрементом затухания δ. Логарифмический декремент затухания есть логарифм отношения двух последовательных амплитуд колебаний отличающихся на период.

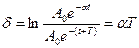(5.30)

При малых значениях δ пользуются понятием добротности .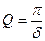

Период затухающих колебаний равен

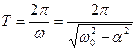
При 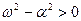система совершает периодические затухающие колебания, как показано на рис.5.8.

Когда 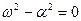, то Τ ® ∞. Это значит, что движение перестает быть периодическим (см. рис.5.8). В зависимости от начальных условий система возвращается в положение равновесия по одной из двух указанных кривых.