Свободные колебания автомобиля с учетом неподрессоренных масс

Ранее были рассмотрены свободные колебания подрессорен­ной массы автомобиля без учета влияния затухания в подвеске и неподрессоренных масс. В действительности затухание в подвеске существует, а неподрессоренные массы в отдельных случаях сопо­ставимы с подрессоренной массой автомобиля. Поэтому необхо­димо учитывать влияние и затухания, и неподрессоренных масс.

При учете влияния неподрессоренных масс автомобиля на сво­бодные колебания подрессоренной массы примем следующие до­пущения:

• связь между колебаниями передней и задней частей кузова
автомобиля отсутствует, т.е. ε_у = 1 (ρ_у² = l₁l₂);

• затухания в подвеске или сопротивления амортизаторов нет (k = 0).
Колебательная система автомобиля, соответствующая приня­-
тым допущениям, представлена

на рис. 13.8.

В указанной колебательной сис­теме М₁ и М₂— приведенные мас­сы, приходящиеся на передние и задние колеса; m₁и m₂ — массы переднего и заднего мостов; с_п1и с_п2— жест-кости передней и задней подвесок; с_ш1 и с_ш2— жесткости шин передних и задних колес.

Массы М₁и М₂связаны между собой шарнирно жестким невесо­мым стержнем. Следовательно, имеются две независимые колеба­тельные системы, соответствую­щие передней и задней частям автомобиля.

Свободные колебания каждой части автомобиля описываются системой уравнений:

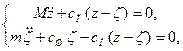
где — вертикальное перемещение неподрессоренной массы. Разделив эти уравнения соответственно на М и т,получим

где 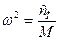— парциальная частота колебаний подрессоренной мас-

сы М при неподвижной неподрессоренной массе m; –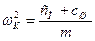

парциальная частота колебаний неподрессоренной массы т при неподвижной подрессоренной массе М.

Из уравнений колебаний колебательной системы автомоби­ля с учетом влияния неподрессоренных масс следует, что каж­дая колебательная система имеет две частоты собственных коле­баний — низкую (ω) и высокую (ω_к). Следовательно, автомо­биль имеет четыре частоты собственных колебаний, прибли­женное значение которых можно определить из следующих вы­ражений:

для подрессоренных масс

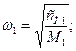
для неподрессоренных масс

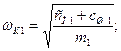
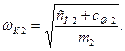
Низкие частоты ω₁и ω₂являются частотами колебаний кузова на упругих устройствах подвески (рессоры, пружины и др.). Для легковых автомобилей эти частоты равны 60... 90 мин^–1, а для гру­зовых — 90... 145 мин^–1.

Высокие частоты ω_к1 и ω_к2 представляют собой частоты колеба­ний передних и задних мостов и колес. Их значения составляют для легковых автомобилей 500...700 мин^–1 и для грузовых — 350...500 мин^–1.

13.8. Свободные колебания автомобиля с учетом затухания

Свободные колебания автомобиля всегда являются затухающими вследствие их гашения в подвеске автомобиля.

Гашение колебаний автомобиля происходит в результате дей­ствия в подвеске трения, которое различно по своей природе и может быть жидкостным (в гидравлических амортизаторах), су­хим (в рессорах и шарнирах подвески) и межмолекулярным (в шинах и резиновых деталях подвески).

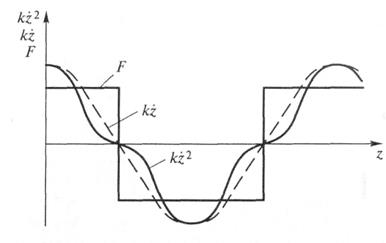
Все перечисленные виды трения различны по абсолютной ве­личине, неодинаково изменяются в зависимости от скорости ко­лебаний автомобиля (рис. 13.9) и поэтому по-разному влияют на затухание колебаний.

Характер изменения указанных видов трения в случае гармо­нических колебаний также различен (рис. 13.10).

Жидкостное трение может изменяться пропорционально как квадрату скорости, так и скорости колебаний. Обычно оно линей­но при малой скорости колебаний и быстро растет с ее увеличе­нием. Даже небольшое жидкостное трение вызывает быстрое зату­хание колебаний.

Межмолекулярное трение пропорционально скорости колеба­ний, но при значительном изменении частоты эффективного за­тухания колебаний не вызывает.

Основным видом трения, которое постоянно действует в под­веске совместно с жидкостным трением амортизаторов, является сухое трение. При эксплуатации сухое трение не остается посто­янным, а все время изменяет­ся, не поддается регулированию и ухудшает плавность хода ав­томобиля. Поэтому в современ­ных автомобилях, прежде всего в легковых и автобусах, стремят­ся устранить сухое трение. Чем больше вклад амортизаторов в гашение колебаний, тем легче добиться желаемого характера затухания колебаний и необхо­димой плавности хода автомо­биля.

Рис. 13.9. Зависимости силы трения сухого (F),жидкостного линей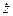но­го (k )и квадратичного (k 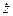2)от скорости колебаний

Рассмотрим свободные коле­бания автомобиля, затухание которых происходит за счет дей­ствия в подвеске различных ви-дов трения. При этом примем следующие ограничения:

Рис. 13.10. Характер изме­нения силы трения сухо­го (F),жидкостного ли­нейного (k 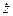)и квадра­тичного (k 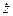²)при гармо­нических колебаниях

• связь между колебаниями передней и задней частей кузова
автомобиля отсутствует (ε_у =1);

• влиянием неподрессоренных масс на колебания кузова пре­
небрегаем.

Колебательная система автомобиля, гашение колебаний подрес­соренной массы которой происходит только за счет действия сухо­го трения, при принятых ограничениях изображена на рис. 13.11, а.

В этой колебательной системе шарнирно соединенные массы М₁и М₂соответствуют весу передней и задней частей кузова авто­мобиля; с₁и с₂— приведенные жесткости передней и задней под­весок; F₁и F₂— динамическая сила сухого трения передней и задней подвесок.

Свободные затухающие колебания передней и задней частей кузова описываются уравнением

.

Из этого уравнения следует, что направление силы сухого тре­ния в процессе колебаний различно и всегда противоположно направлению движения подрессоренной массы.

Исследования влияния сухого трения в подвеске на колебания подрессоренной массы выявили следующее.

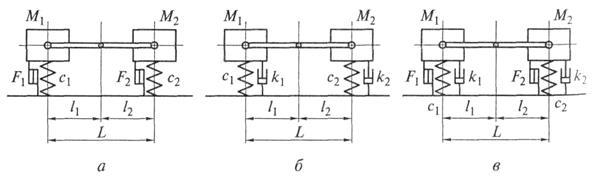
Рис. 13.11. Колебательные системы автомобиля без неподрессоренных

масс при ε_у = 1 с сухим (а), жидкостным (б), одновременно сухим и

жидкостным (в) трением в подвеске

Собственная частота и период колебаний подрессоренной массы ле зависят от значения силы сухого трения. Следовательно, сила сухого трения постоянна по величине и не меняет собственной частоты и периода колебаний подрессоренной массы автомобиля.

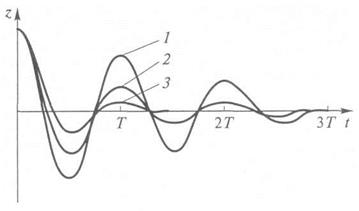
При действии в подвеске сухого трения амплитуда колебаний подрессоренной массы убывает тем быстрее, чем больше значе­ние силы сухого трения. При этом время убывания амплитуды колебаний уменьшается пропорционально возрастанию силы су­хого трения. Кроме того, характер изменения кривой 1 (рис. 13.12) затухающих колебаний свидетельствует о том, что при наличии в подвеске сухого трения и отсутствии других сопротивлений (ви­дов трения) амплитуда колебаний подрессоренной массы за каж­дый период уменьшается на одну и ту же величину, т. е. изменяет­ся по закону арифметической прогрессии.

Основным гасящим устройством в подвеске является гидрав­лический амортизатор, который обеспечивает затухание колеба­ний кузова и колес за счет жидкостного трения. При этом сила трения в амортизаторе для упрощения считается пропорциональ­ной скорости колебаний.

Рассмотрим свободные колебания автомобиля, затухание ко­торых происходит в результате действия только жидкостного тре­ния. Соответствующая колебательная система автомобиля с уче­том принятых ранее допущений приведена на рис. 13.11, б. В этой системе k₁и k₂ – коэффициенты сопротивления передних и зад­них амортизаторов, значение каждого из которых можно опреде­лить по формуле

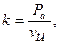
где Р_а — сила сопротивления амортизатора, кг; v_пa — скорость перемещения поршня амортизатора, см/с.

Уравнение свободных затухающих колебаний передней и зад­ней частей кузова автомобиля для случая ε_у = 1 имеет вид

.

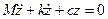Рис. 13.12. Кривые свободных затухающих колебаний под-рессоренной массы при дей­ствии в подвеске сухого (1), жидкостного (2), сухого и жидкостного (3) трения

После деления на приведенную массу М оно записывается в виде

,

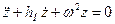где 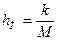— коэффициент сопротивления подвески.

Коэффициент сопротивления амортизатора k не может дать полного представления о затухании колебаний в системе. Так, один и тот же амортизатор в подвесках разных автомобилей с неодина­ковыми подрессоренными массами обеспечивает различный эф­фект. Коэффициент сопротивления подвески h_пдает более полное представление о гашении колебаний в подвеске, так как учитыва­ет величину колеблющейся подрессоренной массы.

Однако наилучшую оценку гашения колебаний в подвеске ав­томобиля обеспечивает относительный коэффициент затухания

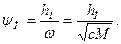
Колебания кузова автомобилей, как показали исследования, происходят с затуханием, при котором ψ_п = 0,15...0,30. При таких значениях коэффициента ψ_п обеспечивается наилучшая плавность хода автомобиля.

Исследования влияния жидкостного трения в подвеске на ко­лебания подрессоренной массы показали следующее.

Изменение собственной частоты и периода колебаний подрес­соренной массы пропорционально скорости колебаний. При уве­личении затухания собственная частота и период колебаний из­меняются незначительно. Амплитуда колебаний подрессоренной массы уменьшается при возрастании затухания в подвеске. Умень­шение амплитуды колебаний происходит тем быстрее, чем силь­нее затухание. При этом время уменьшения амплитуды колебаний пропорционально увеличению затухания.

Характер уменьшения амплитуды колебаний (см. кривую 2 на рис. 13.12) свидетельствует о том, что в результате действия в подвеске жидкостного трения, пропорционального скорости ко­лебаний, уменьшение отклонений подрессоренной массы при колебаниях происходит по закону геометрической прогрессии. Сле­довательно, при возрастании в подвеске силы жидкостного тре­ния происходит быстрое гашение колебаний подрессоренной массы автомобиля.

При наличии связи между колебаниями передней и задней ча­стями кузова автомобиля, когда коэффициент распределения под­рессоренных масс ε_у ≠1 (грузовые автомобили, автобусы), сво­бодные колебания с затуханием будут описываться системой урав­нений:

где 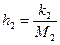– коэффициенты сопротивления передней и задней подвески.

Выше были рассмотрены свободные колебания подрессорен­ной массы автомобиля под действием только сухого или жидко­стного трения, пропорционального скорости колебаний. Однако эти случаи являются частными и не всегда точно отражают про­цесс затухания колебаний, так как их гашение в подвеске автомо­билей происходит в результате совместного действия сухого, меж­молекулярного и жидкостного трения.

Уравнение свободных колебаний передней и задней частей ку­зова автомобиля (для случая ε_у= 1), затухание которых происхо­дит вследствие совместного действия сухого, жидкостного и меж­молекулярного трения (рис. 13.11, в),будет иметь следующий вид:

.

В приведенном уравнении затухание колебаний определяется комплексом членов 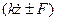,которые представляют собой раз­личные по природе силы сопротивления (трения). При этом на­правление динамической силы сухого трения F в процессе коле­баний различно и всегда противоположно направлению движе­ния подрессоренной массы М.

Исследования показали, что совместное действие в подвеске сухого, жидкостного и межмолекулярного трения приводит к бо­лее интенсивному затуханию колебаний, чем при действии толь­ко трения, пропорционального скорости колебаний. При этом соб­ственная частота и период колебаний подрессоренной массы имеют те же значения, что и в случае действия исключительно трения, пропорционального скорости колебаний.

При совместном гашении колебаний в подвеске различными силами сопротивления (см. кривую 3 на рис. 13.12) амплитуда ко­лебаний подрессоренной массы уменьшается с возрастанием силы сухого трения, причем уменьшение амплитуды происходит тем интенсивнее, чем больше сила сухого трения.