Поперечная устойчивость на вираже
Ранее были рассмотрены случаи, когда нарушение поперечной устойчивости автомобиля вызывали закругления или поперечный уклон дороги. Однако в эксплуатации часто встречаются одновременно поворот и поперечный уклон дороги, что создает предпосылки для нарушения поперечной устойчивости.
На рис. 11.7 представлены два автомобиля. Автомобиль I движется на повороте по наружному краю дороги, а автомобиль II — по внутреннему.
Определим, какой из них более устойчив и безопасен на повороте. Для этого разложим поперечную силу Ру и силу тяжести G на соответствующие составляющие, перпендикулярные (Ру' и G')и параллельные (Руи G") поверхности дороги.
| Рис. 11.7. Движение автомобилей на повороте: G′, G" — составляющие силы тяжести автомобиля на повороте; Р'у, Р′′у — составляющие поперечной силы |
У автомобиля II поперечная устойчивость выше, чем у автомобиля I, так как у него силы Ру' и G' складываются и увеличивают
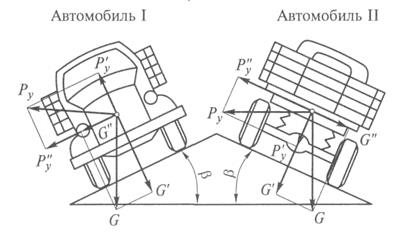
сцепление колес с дорогой, а силы Р''у и G'' частично уравновешивают друг друга, действуя в противоположные стороны.
У автомобиля I силы Р'у и G' направленные в противоположные стороны, уменьшают сцепление колес с дорогой, а силы Р''у и G'', действуя в одном направлении, уменьшают поперечную устойчивость. Таким образом, автомобиль II, движущийся по внутреннему краю дороги (по отношению к центру поворота), более устойчив и безопасен на повороте, чем автомобиль I.
В связи с этим для обеспечения необходимой безопасности движения на дорогах с малым радиусом поворота устраивают вираж — односкатный поперечный профиль, благодаря которому поперечный уклон дороги направлен к центру поворота. В этом случае поперечная устойчивость автомобиля существенно повышается (как у автомобиля II) независимо от направления его движения.
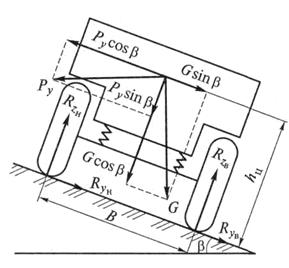
При движении на вираже (рис. 11.8) боковое скольжение автомобиля может начаться при условии
Рб= Рсц,
где Рб — боковая сила, действующая на вираже, или
Руcosβ – Gsinβ = (Руcosβ + Gsinβ)φy.
Подставим в указанное выражение значение поперечной составляющей Ру центробежной силы и, выполнив ряд преобразований, определим критическую скорость автомобиля по заносу на вираже, км/ч:
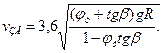
|
Зависимости vзвот R и φу аналогичны приведенным на рис. 11.2. Опрокидывание автомобиля при движении на вираже возможно при условии равенства опрокидывающего и восста-навливающего моментов:
Мо = Мв,
или
(Руcosβ – Gsinβ)hц=
=(Руsinβ + Gcosβ)  .
.
| Рис. 11.8. Движение автомобиля на вираже |
Подставим значение силы Ру и, выполнив соответствующие
преобразования, найдем критическую скорость автомобиля по опрокидыванию на вираже, км/ч:
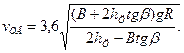
Зависимости vовот радиуса R и высоты hцаналогичны представленным на рис. 11.3.
В приведенных ранее формулах для показателей поперечной устойчивости автомобиля не учитываются эластичность его шин и подвески и, следовательно, поперечный крен кузова. В процессе эксплуатации при действии боковой силы возникает поперечный крен кузова. Угол крена кузова не превышает 8... 10°, но он существенно ухудшает поперечную устойчивость автомобиля, что способствует его опрокидыванию. Так, например, значения критической скорости и критического угла поперечного уклона дороги по опрокидыванию с учетом бокового крена кузова на 10... 15 % меньше, чем без учета крена.
Занос автомобиля
В процессе эксплуатации автомобилей при нарушении поперечной устойчивости чаще происходит их занос, чем опрокидывание. При этом начинают скользить колеса одного из мостов — переднего или заднего.
Определим, что более вероятно и опасно: занос переднего управляемого или заднего ведущего моста.
Для качения колеса без скольжения необходимо, чтобы
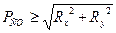 ,
,
где Rx — касательная реакция дороги; Ry — поперечная реакция дороги.
Следовательно, должно выполняться соотношение
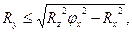
согласно которому поперечная сила, прилагаемая к колесу и не вызывающая его скольжения, тем больше, чем значительнее сила сцепления колеса с дорогой и меньше касательная реакция дороги.
Определим, какое из колес (ведомое, ведущее или тормозящее) наиболее устойчиво против бокового скольжения (заноса).
Ведомое колесо наиболее устойчиво против заноса, так как Касательная реакция дороги Rx,представляющая собой силу сопротивления качению, мала по сравнению с силой сцепления Рсц.
Ведущее и тормозящее колеса менее устойчивы против заноса, поскольку через них передаются соответственно тяговая и тормозная силы. В тот момент, когда сила сцепления будет равна касательной реакции дороги (Рсц = Rx),сцепление колеса с дорогой полностью использовано касательной реакцией. В этом случае достаточно действия небольшой боковой силы, чтобы начался занос колеса. Для ликвидации начавшегося заноса следует уменьшить касательную реакцию на колесе (уменьшить тяговую силу, прекратить торможение).
При прямолинейном движении автомобиля наиболее вероятен занос заднего ведущего моста, так как на его колеса при разгоне и преодолении повышенного сопротивления дороги действуют касательные реакции дороги во много раз более значительные, чем на колеса переднего ведомого моста. При торможении автомобиля вследствие перераспределения нагрузки (увеличивается нагрузка на передний мост) уменьшается сила сцепления задних колес, что также способствует заносу заднего ведущего моста.
|
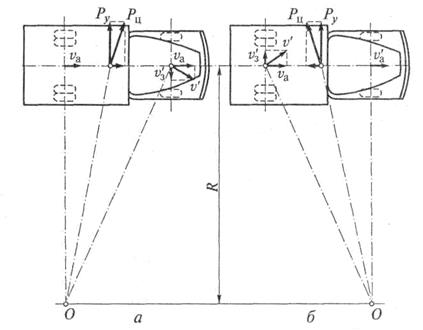
| Рис. 11.9. Занос переднего (а) и заднего (б) мостов автомобиля: О — центр поворота |
Занос заднего ведущего моста автомобиля при эксплуатации не только вероятнее, чем переднего, но и опаснее. Допустим, что у двигавшегося прямолинейно автомобиля со скоростью vaначался занос или переднего (рис. 11.9, а),или заднего (рис. 11.9, б)моста со скоростью v'з. В обоих случаях мост, у которого начался занос, перемещается в направлении результирующей скорости v' а нескользящий мост по-прежнему движется прямолинейно со скоростью vа. Происходит поворот автомобиля вокруг центра О,и на автомобиль действует центробежная сила Рц. Радиус поворота автомобиля в этом случае равен R.
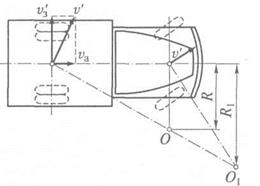
|
Рис. 11.10. Гашение заноса автомобиля:
О, О1 — центры поворота; R, R1 — радиусы поворота при заносе и ликвидации заноса
При заносе переднего моста (см. рис. 11.9, а)поперечная составляющая Ру центробежной силы, являющаяся основной силой, которая действует на автомобиль при повороте, направлена противоположно скольжению передних колес. В результате занос переднего моста автоматически прекращается.
При заносе заднего моста (см. рис. 11.9, б)поперечная составляющая Ру центробежной силы действует в направлении скольжения задних колес и усиливает начавшийся занос заднего моста. Для ликвидации начавшегося заноса необходимо повернуть передние управляемые колеса в сторону заноса, как показано на рис. 11.10. При этом центр поворота автомобиля О переместится в точку О1,радиус поворота увеличится и станет равным R1. В результате поперечная составляющая Ру центробежной силы, способствующая заносу, уменьшится.
При повороте передних колес на больший угол центр поворота переместится на противоположную сторону автомобиля, и поперечная составляющая Ру центробежной силы будет направлена в сторону, противоположную заносу. Занос задних колес в этом случае прекратится.
При еще большем угле поворота передних колес скольжение задних колес начнется в противоположную сторону. Поэтому после прекращения заноса задних колес автомобиль нужно вывести на прямолинейное движение.
В процессе эксплуатации занос автомобиля происходит чаще всего при торможении, когда в месте контакта колес с дорогой действуют большие тормозные силы. В результате колеса теряют способность воспринимать боковые силы. При торможении занос часто возникает также из-за неодинаковых тормозных моментов на колесах одного моста. Это происходит вследствие неправильной регулировки тормозных механизмов или их замасливания и загрязнения.
Для ликвидации начавшегося заноса при торможении следует уменьшить касательные реакции дороги на колесах (прекратить торможение). Для устранения потери устойчивости автомобиля необходимо перед началом поворота уменьшить скорость движения, так как поперечная составляющая Ру центробежной силы пропорциональна квадрату скорости.
11.4. Продольная устойчивость автомобиля
При нарушении продольной устойчивости автомобиль может опрокинуться относительно оси передних или задних колес, а также скользить в продольном направлении.
Опрокидывание вокруг осей колес возможно только у автомобиля с очень короткой базой и высоким расположением центра тяжести. Однако для большинства современных автомобилей, имеющих низкое расположение центра тяжести, опрокидывание в продольной плоскости маловероятно. Возможно лишь продольное скольжение, вызванное буксованием ведущих колес, что более вероятно для автопоездов.
В связи с этим показателем продольной устойчивости автомобиля является критический угол подъема по буксованию αб.
Определим критический угол подъема по буксованию для автомобиля. С этой целью рассмотрим равномерное движение автомобиля на максимальном подъеме (рис. 11.11), так как разгон на нем невозможен. При преодолении максимального подъема скорость движения автомобиля небольшая, поэтому силой сопротивления воздуха Рв пренебрегаем. При этом сцепление ведущих колес с дорогой полностью используется касательной реакцией дороги (Rх2 = Рсц = Rz2φx),а касательной реакцией дороги на передних колесах пренебрегаем, так как она мала по сравнению с касательной реакцией Rx2.
Из условий равновесия автомобиля следует, что
Rz2 L = Ghц sin α+ Gl1cos α; Rx2 = G sin α.
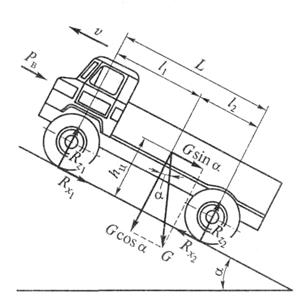
|
Максимальное значение касательной реакции дороги на ведущих колесах автомобиля ограничена сцеплением колес с дорогой:
Rх2 = Rz2φx.
Подставим в это выражение значения реакций дороги Rz2и Rх2и разделим обе части уравнения на cosα. Учитывая в данном случае, что α=αб, определим критический угол подъема по буксованию:
| Рис. 11.11. Схема для определения критического угла подъема по буксованию |
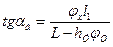 .
.

|
Критическим углом подъема по буксованию называется предельный угол, при котором еще возможно движение автомобиля на подъеме без буксования ведущих колес.
| Рис. 11.12. Зависимости критического угла подъема по буксованию от коэффициента сцепления: 1 — автопоезд; 2 — автомобиль обычной проходимости; 3 — автомобиль повышенной проходимости |
Критический угол подъема по буксованию во многом зависит от коэффициента сцепления φx. Так, например, при φx = 0,3 (асфальт влажный и грязный или покрытый снегом) для автомобилей с колесной формулой 4×2 угол αб = 10...
15°.
Для автомобиля со всеми ведущими колесами критический угол подъема по буксованию
tg αб = φx.
Следовательно, такого типа автомобили могут преодолевать крутые подъемы без потери продольной устойчивости.
Угол αб линейно зависит от коэффициента φx (рис. 11.12).
Дата добавления: 2021-12-14; просмотров: 702;











