Кинематическая энергия манипулятора

Зная скорость произвольной точки каждого звена манипулятора, найдём кинетическую энергию i-го звена.

Обозначим через 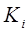кинетическую энергию i-го звена (i=1, 2, …, n). Пусть 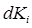кинетическую энергию элемента массы dm i-го звена. Тогда:

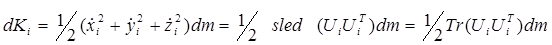. (10-1)

Здесь вместо скалярного произведения используется оператор 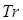(след матрицы 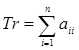), что в дальнейшем позволит перейти к матрице инерции 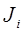i-го звена.

Подставляя в выражение (10-1) значение 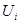из равенства (9-20), получим выражение для кинетической энергии элемента массой dm:

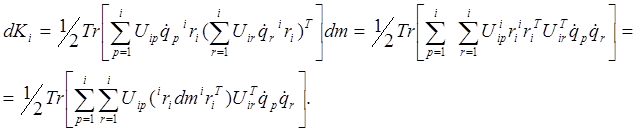(10-2)

Матрица 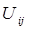характеризует положение точки i-го звена относительно базовой системы координат, обусловленное изменением координаты .

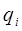Данная матрица одинакова для всех точек i-го звена и не зависит от распределения массы в этом звене, также как и 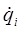. Таким образом:

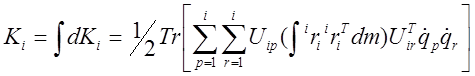. (10-3)

Интегральный член в скобках представляет собой матрицу инерции 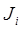i-го звена:

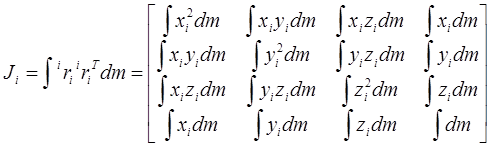. (10-4)

Преобразуя выражения, получим:

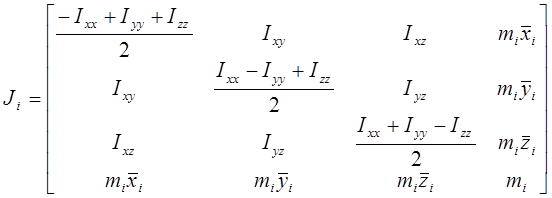, (10-5)

где 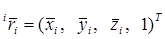однородные координаты центра масс i-го звена в i-й системе координат;

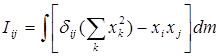- тензор инерции, где i, j, k принимают значения x_i, y_i, z_i (оси i-ой системы координат), а 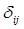- символ Кроникера.

Формулу (6-26) можно также записать в виде:

. (10-6)

Здесь 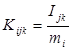и j, k=1, 2, 3, а 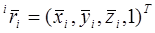- радиус вектор центра масс i-го звена в системе координат i-го звена. Таким образом, полная кинетическая энергия манипулятора равна:

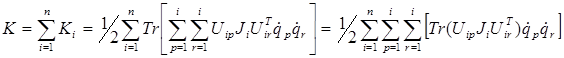. (10-7)

Отметим, что величина J_i (i=1, 2,…, n) зависит только от распределения массы i-го звена в i-й системе координат и не зависит ни от положения, ни от скорости звеньев. Это позволяет однажды вычислив матрицу J_i, использовать полученное значение в дальнейшем для вычисления кинетической энергии манипулятора.