Уравнения вида конфигурации для определения индикаторов конфигурации манипулятора
Полученное решение обратной задачи кинематики для манипулятора типа Пума не единственно и зависит от индикаторов конфигурации, задаваемых исследователем. Эти индикаторы можно определить, зная присоединяемые углы.
Для индикатора РУКА, следуя определению ПРАВОЙ/ЛЕВОЙ руки, уравнение конфигурации можно записать в виде:
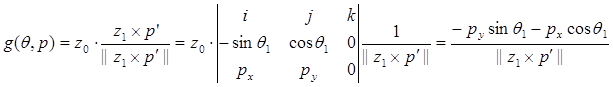 ,
,
(9-1)
где 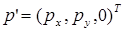 - проекция вектора p(равенство (7-7)) на плоскость
- проекция вектора p(равенство (7-7)) на плоскость 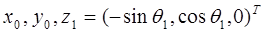 -третий столбец матрицы
-третий столбец матрицы  и
и 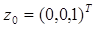 .
.
Возможны следующие варианты:
1) Если 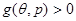 , реализована конфигурация ПРАВОЙ руки.
, реализована конфигурация ПРАВОЙ руки.
2) Если 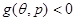 , реализована конфигурация ЛЕВОЙ руки.
, реализована конфигурация ЛЕВОЙ руки.
3) Если 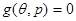 , конфигурация манипулятора одновременно соответсвует определению как ПРАВОЙ, так и ЛЕВОЙ руки: манипулятор находится внутри цилиндра радиусом d2 (рис. 7.1). В этом случае принимается для определённости, что реализована конфигурация правой руки (РУКА=+1).
, конфигурация манипулятора одновременно соответсвует определению как ПРАВОЙ, так и ЛЕВОЙ руки: манипулятор находится внутри цилиндра радиусом d2 (рис. 7.1). В этом случае принимается для определённости, что реализована конфигурация правой руки (РУКА=+1).
Поскольку знаменатель выражения (9-1) всегда положителен, определение ЛЕВОЙ/ПРАВОЙ конфигурации сводится к определению знака числителя 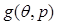 :
:
РУКА= 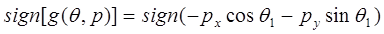 , (9-2)
, (9-2)
где функция sign определена равенством (8-14). Подстановкой первой и второй компонент вектора р из равенства (7-7) в равенство (9-2) получаем:
РУКА= 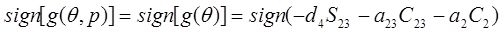 , (9-3)
, (9-3)
Следовательно, из уравнения (9-3) значение индикатора РУКА для ПРАВОЙ/ЛЕВОЙ конфигурации манипулятора устанавливается выражением:
РУКА= 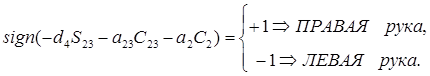 (9-4)
(9-4)
При выводе уравнения конфигурации для индикатора ЛОКОТЬ используем определение ВЕРХНЕЙ/НИЖНЕЙ руки. Взяв 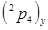 и индикатор РУКА из табл. 7.1, получим уравнение конфигурации для индикатора ЛОКОТЬ, использующее знак второй компоненты вектора положения матрицы
и индикатор РУКА из табл. 7.1, получим уравнение конфигурации для индикатора ЛОКОТЬ, использующее знак второй компоненты вектора положения матрицы 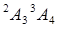 и индикатор РУКА:
и индикатор РУКА:
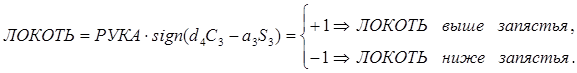 (9-5)
(9-5)
Для индикатора ЗАПЯСТЬЕ, следуя определению возможных конфигураций запястья (КИСТЬ ВВЕРХ/ВНИЗ), сформируем скалярное произведение единичных векторов s и у5 (или z4).
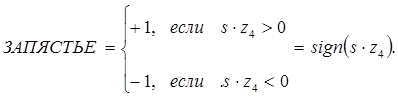 (9-6)
(9-6)
Если 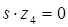 , значение индикатора ЗАПЯСТЬЕ можно определить из выражения:
, значение индикатора ЗАПЯСТЬЕ можно определить из выражения:
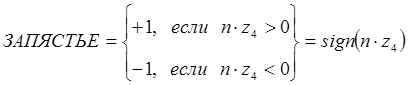 . (9-7)
. (9-7)
Объединив равенства (9-6) и (9-7), получим:
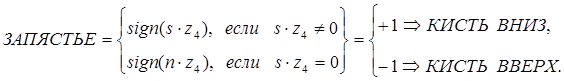 (9-8)
(9-8)
Полученные уравнения конфигурации позволяют проверить решения обратной задачи кинематики. С их помощью при решении прямой задачи кинематики вычисляются значения индикаторов конфигурации, которые затем используются для решения обратной задачи кинематики (рис. 9.1).
Дата добавления: 2021-11-16; просмотров: 768;











