Метод Лагранжа-Эйлера
Полное описание движения манипулятора можно получить, применяя метод Лагранжа-Эйлера для неконсервативных систем. Описав кинематику манипулятора с помощью матричного представления Денавита-Хартенберга, можно получить уравнение динамики. Такое совместное использование Д-Х-представления и метода Лагранжа приводит к компактной векторно-математической форме уравнений движения, удобной для аналитического исследования и допускающей реализацию на ЭВМ.
Вывод уравнений динамики движения манипулятора основан на следующем:
1. На описании взаимного пространственного расположения систем координат i-го и (i-1)-го звеньев с помощью матрицы преобразования однородных координат 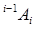 . Эта матрица преобразует координаты произвольной точки относительно i-й системы координаты этой же точки относительно (i-1)-й системы координат.
. Эта матрица преобразует координаты произвольной точки относительно i-й системы координаты этой же точки относительно (i-1)-й системы координат.
2. На использовании уравнения Лагранжа-Эйлера:
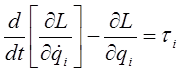 ;
; 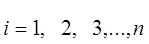 , (9-9)
, (9-9)
где L-функция Лагранжа (L=K-P);
K-полная кинетическая энергии манипулятора;
P-полная потенциальна энергия манипулятора
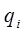 -обобщённые координаты манипулятора;
-обобщённые координаты манипулятора;
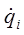 -первая производная по времени обобщённых координат;
-первая производная по времени обобщённых координат;
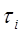 -обобщённые силы (или моменты), создаваемые в i-м сочленении для реализации заданного движения i-го звена.
-обобщённые силы (или моменты), создаваемые в i-м сочленении для реализации заданного движения i-го звена.
Для того, чтобы воспользоваться уравнением Лагранжа-Эйлера, необходимо выбрать систему обобщённых координат. Обобщённые координаты представляют собой набор координат, обеспечивающий, полное описание положения рассматриваемой физической системы в абсолютной системе координат. Существуют различные системы обобщенных координат, пригодные для описания простого манипулятора с вращательными и поступательными сочленениями. Однако, поскольку углы поворотов в сочленениях непосредственно доступны измерению с помощью потенциометров или других датчиков, то они составляют наиболее естественную систему обобщенных координат. В этом случае обобщённые координаты совпадают с присоединенными переменными манипулятора. В частности, если i-е сочленение вращательное, то 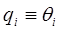 , если же i-е сочленение поступательное, то
, если же i-е сочленение поступательное, то 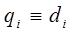 .
.
Дата добавления: 2021-11-16; просмотров: 717;











