Логические функции и способы их записи

В устройствах цифровой электроники используются элементы, входные и выходные сигналы которых могут принимать только два значения, соответствующие логической 1 («1») и логическому 0 («0»). Такие элементы называют логическими. С их помощью реализуют простейшие операции с двоичными числами (то есть с числами двоичной системы счисления).

Для описания алгоритмов работы и структуры цифровых схем используют аппарат алгебры логики (или булевой алгебры – по имени разработавшего ее в середине XIX века ирландского математика Д. Буля). В ее основе лежат три логические операции над логическими переменными:

- логическое отрицание (операция НЕ, инверсия), обозначаемое надчеркиванием над логической переменной или логическим выражением, например , 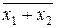и т. д.;

- логическое сложение (операция ИЛИ, дизъюнкция), обозначаемое знаком «+» или «Ú»;

- логическое умножение (операция И, конъюнкция), обозначаемое одним из знаков: «´», «×», «&», «Ù» или отсутствием какого-либо знака между переменными, например х₁х₂.

Логическими переменными (булевыми переменными) называются переменные х₁, х₂, …, х_п, которые могут принимать только два значения – 0 и 1, то есть х_i Î {0, 1}.

Совокупность п логических переменных называется набором переменных и обозначается х₁, х₂, …, х_п. В общем случае может быть 2^п наборов логических переменных.

Логической функцией (булевой функцией) называется функция логических переменных f(x₁, х₂, ..., х_п), которая так же как и ее аргументы принимает только значения 0 и 1.

Каждая логическая операция задает соответствующую логическую функцию своих переменных. Следовательно, можно говорить о трех логических функциях: конъюнкции(y=х₁×х₂×…×х_п), дизъюнкции(y=х₁+x₂+…+х_п), инверсии (y= ). Число аргументов (переменных) функций дизъюнкции и конъюнкции в общем случае может быть произвольным (больше двух).

Система логических функций называется функционально полной, если при помощи функций, входящих в систему, можно выразить любую сколь угодно сложную булеву функцию.

В математической логике доказывается, что если система булевых функций содержит функции конъюнкцию, дизъюнкцию и инверсию, то она является функционально полной.

Функциональной полнотой обладают и некоторые другие системы, например, система, состоящая из одной логической функции И – НЕ («штрих Шеффера», ) и система, содержащая единственную логическую функцию ИЛИ – НЕ («стрелка Пирса», ).

Логическую функцию можно описать несколькими способами:

-в словесной форме;

-с помощью таблицы;

-с помощью алгебраического выражения (в аналитическом виде);

-с помощью последовательности десятичных чисел и др.

Табличное представление логической функции является наиболее наглядным. Таблица, с помощью которой описывают логическую функцию, называется таблицей истинности. Пример таблицы истинности функции у = f(х₁, х₂) двух переменных показан на рисунке 5.4. Число строк в таблице истинности равно 2^п, где п – число логических переменных.

Рисунок 5.4 – Таблица истинности логической функции у = f(х₁, х₂)

В первом столбце таблицы истинности записаны номера наборов логических переменных, численно равные десятичному эквиваленту двоичного числа x_пx_п-1 … x₂x₁, составленного из значений логических переменных (второй и третий столбцы). В последнем столбце записаны значения логической функции на соответствующих наборах логических переменных.

В общем случае логическая функция может быть определена не на всех наборах логических переменных (то есть может быть недоопределенной). Некоторых сочетаний значений логических переменных на входе цифрового устройства, описываемого логической функцией, может просто не существовать. В этом случае набор переменных называется запрещенным, а в таблице истинности напротив запрещенного набора вместо значения функции обычно записывают знак «*» (рисунок 5.5). В приведенном примере запрещенными являются наборы логических переменных с номерами 2, 5 и 6.

Логические функции от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В таблице 5.1 приведены все возможные логические функции двух переменных.

Для аналитической записи логических функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля.

Рисунок 5.5 – Пример таблицы истинности недоопределенной

логической функции

Таблица 5.1

fi	х2					Название функции	Вид функции
х1
f0						Константа 0	f0(x1, x2) = 0
f1					Конъюнкция	f0(x1, x2) = x1×x2
f2					Функция запрета по x2	f0(x1, x2) =
f3					Переменная x1	f0(x1, x2) = x1
f4					Функция запрета по x1	f0(x1, x2) =
f5					Переменная x2	f0(x1, x2) = x2
f6					Cложение по модулю два	f0(x1, x2) =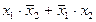
f7					Дизъюнкция	f0(x1, x2) = x1+x2
f8					Стрелка Пирса	f0(x1, x2) =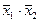
f9					Функция равнозначности	f0(x1, x2) =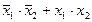
f10					Инверсия x2	f0(x1, x2) =
f11					Импликация от x1к x2	f0(x1, x2) =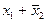
f12					Инверсия x1	f0(x1, x2) =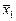
f13					Импликация от x2 к x1	f0(x1, x2) =
f14					Штрих Шеффера	f0(x1, x2) =
f15					Константа 1	f0(x1, x2) = 1

Конституентой единицы называется такое логическое произведение (конъюнкция) п переменных одного набора, в которое каждая переменная входит только один раз в прямой или инверсной форме. Переменная, принимающая на данном наборе значение «1», записывается в конституенте единицы в прямом виде, а значение «0» – в инверсном виде.

Отличительной особенностью конституенты единицы является то, что она равна «1» только на одном вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом т_i, где индекс i указывает на номер набора, на котором конституента единицы равна «1».

Например, для нулевого набора логических переменных (рисунок 5.4) конституента единицы имеет вид

,

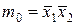а для второго набора – соответственно вид

.

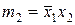В общем случае можно записать 2^п конституент единицы, где п – число логических переменных в наборах.

Конституентой нуля п переменных одного набора называется логическое сложение (дизъюнкция) этих переменных, которое обращается в «0» лишь при одном наборе логических переменных. При этом в прямом виде в конституенте нуля записывают переменные, принимающие на данном наборе значение «0», а в инверсном – значение «1». Будем обозначать конституенту нуля символом р_i, где индекс i указывает на номер набора, на котором конституента нуля равна «0». Например, для нулевого набора логических переменных (рисунок 5.4) конституента нуля имеет вид

,

а для первого набора – соответственно вид

.

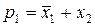Аналитическая запись логической функции может быть выполнена в виде совершенной дизъюнктивной или совершенной конъюнктивной нормальной формы.

Совершенной дизъюнктивной нормальной формой(СДНФ) логической функции называется дизъюнкция всех конституент единицы для тех наборов логических переменных, на которых логическая функция принимает значение «1».

Запись СДНФ логической функции осуществляется непосредственно по данным, внесенным в таблицу истинности. Например, воспользовавшись рисунком 5.4, запишем СДНФ логической функции у:

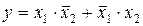. (5.1)

Совершенной конъюнктивной нормальной формой(СКНФ) логической функции называется конъюнкция всех конституент нуля для тех наборов логических переменных, на которых логическая функция принимает значение «0». Следовательно, для функции у (рисунок 5.4) СКНФ будет иметь вид

. (5.2)

Тождественные преобразования логических функций для получения их оптимального вида осуществляют на основе законов и тождеств алгебры логики.