Минимизация логических функций
При проектировании логического устройства необходимо стремиться к тому, чтобы достичь поставленной цели с минимальными затратами. Это означает, что синтезируемая схема должна содержать минимально необходимое количество логических элементов с как можно меньшим числом входов. Для выполнения этих условий логическое выражение, используемое при синтезе, должно содержать минимальное число элементарных конъюнкций или дизъюнкций и минимально возможное число переменных в этих конъюнкциях (дизъюнкциях). СДНФ и СКНФ логической функции не удовлетворяют этим требованиям. Поэтому, прежде чем приступить к разработке функциональной схемы логического устройства, нужно получить минимальную форму логической функции. ДНФ (КНФ) называется минимальной, если она содержит минимальное число букв. Чтобы получить минимальную форму логической функции, ее необходимо минимизировать.
Существует несколько методов минимизации логических функций:
-метод непосредственных преобразований;
-метод Карно-Вейча;
-метод Квайна и Мак-Класки.
Метод непосредственных преобразований основан на применении с целью минимизации логической функции аксиом и теорем алгебры логики. Результатом минимизации должна стать тупиковая форма логической функции, то есть такое логическое выражение, к слагаемым которого больше не могут быть применены операции склеивания. Следует иметь в виду, что для одной функции может существовать несколько тупиковых форм. Но не каждая тупиковая форма является минимальной. Минимальной формой является тупиковая форма логической функции минимальной длины. В общем случае чтобы найти минимальную форму необходимо перебрать все тупиковые формы.
Метод непосредственных преобразований не всегда удобен при практическом выполнении минимизации. Метод Квайна и Мак-Класки состоит в применении для минимизации логической функции ЭВМ. Его использование целесообразно, когда число входных переменных превышает 6 – 7. При незначительном числе аргументов минимизацию логической функции чаще всего выполняют методом Карно-Вейча. Рассмотрим его сущность.
Диаграмма Вейча (карта Карно) является упрощенной формой записи таблицы истинности логической функции. Основное отличие между диаграммой Вейча и картой Карно состоит в нумерации строк и столбцов таблицы. Рассмотрим методику минимизации логической функции с помощью диаграммы Вейча.
В общем случае число клеток диаграммы Вейча составляет 2п, где п – число входных переменных. Каждой комбинации входных переменных (набору входных переменных) можно поставить в соответствие только одну клетку диаграммы. В клетку записывается значение логической функции (0 или 1) на данном наборе. В клетку, соответствующую запрещенному набору входных переменных, записывается знак «*». Входные переменные располагаются по внешним сторонам диаграммы напротив ее строк и столбцов. При этом значение каждой из входных переменных относится ко всей строке или ко всему столбцу. На рисунке 5.6 приведены примеры диаграмм Вейча для логических функций двух, трех и четырех переменных.
| х2 | 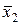
|
х2 |
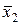
| |||||||||||
| х1 | х1 | |||||||||||||
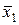
| 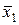
| |||||||||||||
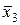
|  х3 х3
| 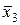
|
х2 |
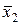
| ||||||||
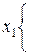
| 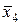
| ||||||||
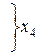
| |||||||||
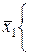
| |||||||||
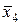
| |||||||||
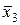
|  х3 х3
| 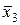
| |||||||
Рисунок 5.6 – Примеры диаграмм Вейча
Цифры, записанные в клетки диаграмм Вейча на рисунке 5.6, представляют собой номера наборов переменных в таблице истинности.
При склеивании переменных нужно руководствоваться следующими правилами:
а) все клетки, содержащие единицы (при записи функции в дизъюнктивной форме) или нули (при записи в конъюнктивной форме), должны быть замкнутыми в прямоугольные контуры. Единичные контуры могут объединять несколько единиц, но не должны содержать внутри себя нулей. Нулевые контуры могут объединять несколько нулей, но не должны содержать внутри себя единиц. Одна и та же единица (или ноль) может одновременно входить в несколько единичных (нулевых) контуров. Число клеток в контуре равняется 2i, где i = 0, 1, 2, 3, 4, ...;
б) в контуры можно объединять только соседние клетки, которые содержат единицы (нули). Соседними (рядом расположенными) считаются, в том числе, клетки, расположенные на противоположных сторонах диаграммы (в противоположных строках или столбцах);
в) каждой единичной клетке отвечает конъюнкция логических переменных, которые определяют данную клетку. Каждой нулевой клетке отвечает дизъюнкция инверсий логических переменных, что определяют данную клетку;
г) выражения, которые отвечают контурам, не содержат тех переменных, чьи границы пересекаются площадью, ограниченной данным контуром (другими словами, те переменные, которые в данном контуре имеют и прямое и инверсное значение – склеиваются);
д) выражение логической функции может быть записано по соответствующей ей диаграмме Вейча в дизъюнктивной или конъюнктивной форме. Дизъюнктивная форма составляется в виде дизъюнкции конъюнкций, которые отвечают единичным контурам, выделенным на диаграмме для определения функции; конъюнктивная – в виде конъюнкции дизъюнкций, которые отвечают нулевым контурам;
е) для контуров, которые охватывают разное количество клеток, получаются выражения разной сложности. Поэтому для данной логической функции можно записать по ее диаграмме Вейча несколько алгебраических выражений, которые отличаются по сложности. Наиболее сложное выражение получают в том случае, когда каждой клетке отвечает свой отдельный контур. Это выражение представляет собой СДНФ или СКНФ данной функции.
Для получения по диаграмме Вейча минимального выражения логической функции следует руководствоваться правилом: единицы и нули должны объединяться минимальным числом наибольших контуров.
Рассмотрим пример минимизации логической функции трех переменных у = f(x1, x2, x3), заданной таблицей истинности (рисунок 5.5), воспользовавшись методом Карно-Вейча. Для начала воспользуемся представлением функции в дизъюнктивной нормальной форме. В этом случае диаграмма Вейча должна быть заполнена, как показано на рисунке 5.7.

Рисунок 5.7 – Минимизация функции к виду ДНФ
Из рисунка 5.7 видно, как можно наилучшим образом объединить единицы в единичные контуры. При этом в контуры могут входить и ячейки с номерами запрещенных наборов (то есть элементами которых являются «*»). В результате такого объединения получим тупиковую форму логической функции в виде дизъюнкции конъюнкций (число которых равно числу единичных контуров) входных переменных, которые не склеились:
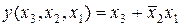 . (5.3)
. (5.3)
Если для представления логической функции после минимизации выбрана конъюнктивная нормальная форма, то в диаграмме Вейча объединяют нули в нулевые контуры. Как и в предыдущем случае, в нулевые контуры могут быть включены ячейки, элементами которых являются «*» (рисунок 5.8).

Рисунок 5.8 – Минимизация функции к виду КНФ
Тупиковая форма логической функции после минимизации представляет собой конъюнкцию дизъюнкций (число дизъюнкций равно числу нулевых контуров) инверсных значений тех входных переменных, которые не склеились:
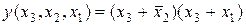 . (5.4)
. (5.4)
Выражения (5.3) и (5.4) описывают структуру логического устройства, алгоритм функционирования которого задан функцией у (рисунок 5.5). Несмотря на то, что полученные выражения разные по виду, а, следовательно, и схема логического устройства в каждом случае будет выполнена по разному, сигналы на выходах этих схем на одних и тех же номерах разрешенных наборов входных переменных будут одинаковы.
Дата добавления: 2021-11-16; просмотров: 776;











