Априорные процедуры многокритериальной оптимизации

Идея всех априорных процедур – это сведение задачи многокритериальной оптимизации к задаче однокритериальной оптимизации, потому что методы для решения задач однокритериальной оптимизации хорошо разработаны.

В процедурах априорного типа делается явное или неявное предположение, что вся информация, позволяющая определить наилучшее решение, скрыта в формальной модели задачи, т.е. в описании множества альтернатив и целевых функций. Следовательно, с помощью некоторых преобразований эта информация может быть извлечена из этой формальной модели и конструктивно использована. Традиционная схема рассуждений в значительно упрощенном виде выглядит следующим образом.

Каждый критерий f_i( 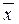) i = 1, 2, …, r характеризует некоторое локальное качество на множестве альтернатив G_x, например, вес, надежность, стоимость, быстродействие и т.д. Наилучшая альтернатива, по-видимому, характеризуется наиболее удачным сочетанием всех этих локальных качеств, т.е. имеет максимальное значение «глобального» качества. Таким образом, для выбора наилучшей альтернативы достаточно понять, каким образом глобальное качество зависит от локальных качеств, после чего многокритериальная задача будет сведена к задаче скалярной оптимизации.

Понятно, что вид глобальной функции качества существенно зависит от типа решаемой задачи.

Остановимся здесь на некоторых наиболее часто применяемыхспособах построения глобальной функции качества, т.е. на преодолении неопределенности цели.

Пусть задача многокритериальной оптимизации имеет вид:

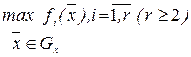(6.5)

а). Простейший способ преодоления неопределенности цели (выделение главного критерия)

Очень часто в задачах проектирования задается некоторая система нормативов 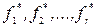. Это значит, например, что параметры будущей конструкции должны быть таковы, чтобы максимизировать функции f_i( ) при условиях:

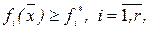(6.6)

где 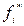– некоторая система контрольных показателей.

Предположим, что, помимо того, среди критериев f_i мы выделили некоторый главный, например, f₁( 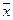). Тогда мы приходим к однокритериальной задаче:

Найти f₁( 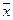) → max (6.7)

при условии: 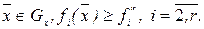(6.8)

Даннаясхема сведения задачи (6.5) к однокритериальной задаче (6.7)–(6.8) является, вероятно, самой простой и наиболее употребительной в инженерной практике. Недостатками этого способа являются трудности выбора главного критерия и определения критериальных ограничений (назначения допустимых границ используемых показателей 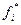). Также к недостаткам нужно отнести возможность варианта, что введенные ограничения окажутся несовместными.

Если задача (6.7)–(6.8) разрешима, то ее решение принимается в качестве решения задачи (6.5), либо на основе полученного решения (например, при помощи двойственных оценок ограничений) устанавливаются новые пределы 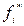,( 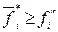) и задача решается снова.

Если задача (6.7)–(6.8) решения не имеет, то приходится назначать новые пределы 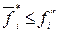и задачу перерешать с 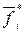вместо .

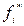Задача проектировщика в данном подходе сводится только к назначению допустимых границ используемых показателей.

б). Линейная свертка

Вместо r частных критериев f_i( ) предлагается рассматривать один критерий вида:

F( ) = 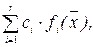(6.9)

где c_i ≥ 0 и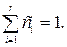

Такой способ свертки вводит, по существу, отношение эквивалентности различных критериев, таккак величины c_i показывают, насколько изменяется целевая функция F( ) приизменении критерия f_i( ) на единицу.

Коэффициенты c_i – результаты экспертизы,они отражают представление лица, принимающего решение о содержании компромисса, который он вынужден принять.

Если же критерии f_i( 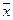) не выражаются в одних и тех же единицах измерения, то для использования формулы (6.9)их приводят к безразмерному виду. Известны разные способы. Например, путем деления каждого критерия на его максимальное значениена допустимом множестве G_x:

F( ) =

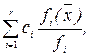
где f_i – максимальные значенияфункций f_i ( ) i = 1, 2, …, r на G_x.

Более сложный способ – введение функции:

F( ) =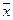

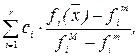
где f_i^M – максимальное, а f_i^m – минимальное значения критерия f_i ( 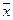) на G_x. При этом вклад «локального» качества f_i( ) в «глобальное» качество F( ) зависит от того, насколько сильно меняется локальное качество на допустимом множестве G_x.

в). Принцип справедливого компромисса

Основным недостатком предыдущего способа является возможность компенсации недопустимо малых значений некоторых критериев достаточно большими значениями других. Действительно, если характеризует проект самолета, а критерии f₁ и f₂ представляют собой его надежность и скорость, соответственно, то очень высокой надежностью может обладать самолет, который никогда не сможет взлететь, и, следовательно, будет иметь нулевую скорость. Несмотря на явную бесполезность такого устройства, значение функции

F( ) = с₁·f₁( ) + с₂·f₂( )

может быть довольно большим.

В таких случаях необходимо использовать другие принципы, например,

F( ) = .

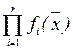Этот принцип получил название принципа справедливого компромисса. Применение этого обобщенного критерия позволяет преодолеть указанные недостатки (например, присваивает нулевое значение качества самолету, который не может летать).

г). Принцип гарантированного результата

Предположим, что мы ввели некоторую систему контрольных показателей f_i^*, относительно которых критерии f_i( ) должны удовлетворять условиям f_i ( ) ≥ f_i^*, i = 1, 2, …, r.

В таких случаях целевую функцию удобно представлять ввиде:

F( ) =

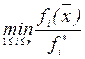
и искать вектор ,который обеспечивает максимальное значение F( ). Смысл здесь достаточно прост. При данном значении вектора 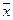величина F( ) даетнам значение наихудшего из показателей f_i( ). Максимизация F( ) обеспечивает наибольшее значение для наихудшего из показателей f_i( ) т.е. гарантированный результат.

д). Метод идеальной точки в пространстве критериев

Предположим, что мы решилисистему однокритериальных задач

f_i ( ) ® max, i = 1, 2, …, r,

и нашли идеальную точку 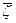= (x_1,…_, x_n), где x_i =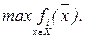

Точка 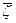является недостижимой в пространстве критериев. Введем положительно определенную матрицу R={r_ij}. Тогда скалярная величина

H= 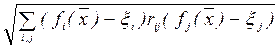(6.10)

определяет некоторое расстояние от точки, соответствующей данному вектору , до идеальной точки. В частном случае, когда R – единичная матрица

H =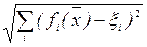

есть евклидово расстояние до точки .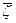

В качестве нового скалярного критерия мы можем принять функцию (6.10). Ее минимизация дает определенную полезную информацию: показывает наши предельные возможности достижения идеальной точки.

е). Метод ранжирования критериев

Предположим, что локальные критерии упорядочены по важности:

f₁( ) > f₂( ) >… > f_r( ),

здесь (f_i( ) > f_i+1( )) означает, что f_i( ) важнее f_i+1( ).

Тогда решение задачи сводится к тому, чтобы

найти max f₁( ) = f₁^*;

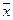
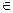G_x

найти max f₂( ) = f₂^* при f₁( ) = f₁^*;

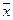
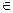G_x

и т. д;

найти max f_n( ) = f_n^* при f_i( 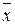) = f_i^*, i = 1, 2 ,…, r - 1,

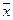
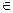G_x

т.е. к многоэтапному алгоритму с оптимизацией каждого критерия при фиксированных предыдущих критериях.

На практике для получения приемлемых решений по менее важным критериям приходится делать уступки по другим, наиболее важным. Данный подход реализуется в алгоритме последовательных уступок, который сводится к последовательному решению задач однокритериальной нелинейной оптимизации:

найти f₁^* = max f₁( );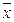

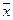
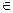G_x

найти f₂^* = max f₂( ) при f₁( ) ≥ f₁^*- ∆₁

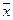
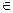G_x

и т. д.;

найти f_r^* = max f_r( 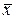) при f_i( 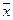) ≥ f_i^*- ∆_i , i = 1, 2, …, r-1.

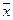
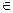G_x,

где ∆_i – величина уступки по i–му критерию.

Другими словами, решается скалярная задача оптимизации по критерию f₁( ). Если max f₁( ) = f₁^*, то по критерию f₁( ) устанавливается уступка ∆_1, на которую согласно ЛПР, чтобы упростить решение по следующим критериям (в первую очередь, по f₂( )) и т. д.

Следовательно, процедуры рассмотренного типа основаны на предположении возможности априорного (до решения задачи) определения наилучшего соотношения между требованиями, предъявляемыми различными критериями. Понятно, что такая возможность существует далеко не всегда. Кроме того, выбор конкретного вида глобальной функции цели не может быть произведен в отрыве от решаемой задачи.

Следует отметить, что методы сведения задач МКО к однокритериальным, могут быть выбраны по разному, и заранее неизвестно, который из них окажется более подходящим для решения данной задачи (окончательное решение в выборе метода остается за ЛПР).