Меры центральной тенденции

К первичным описательным статистикам обычно относят числовые характеристики распределения измеренного на выборке признака. Каждая такая характеристика отражает в одном числовом значении свойство распределения множества результатов измерения: с точки зрения их расположения на числовой оси либо с точки зрения их изменчивости. Основное назначение каждой из первичных описательных статистик − замена множества значений признака, измеренного на выборке, одним числом (например, средним значением как мерой центральной тенденции). Компактное описание группы при помощи первичных статистик позволяет интерпретировать результаты измерений, в частности, путем сравнения первичных статистик разных групп.

Мера центральной тенденции − это число, характеризующее выборку по уровню выраженности измеренного признака.

Существуют три способа определения «центральной тенденции», каждому из которых соответствует своя мера: мода, медиана и выборочное среднее.

Мода (Mo) − это такое значение из множества измерений, которое встречается наиболее часто. Моде, или модальному интервалу признака, соответствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.

Пример.Среди 8 значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо = 7 как наиболее часто встречающееся значение. В таблице 4.2 предыдущей темы Мо = 3, а в таблице 4.3 модальным является интервал 50-54.

Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений.

Распределение может иметь и не одну моду. Когда все значения встречаются одинаково часто, принято считать, что такое распределение не имеет моды.

Бимодальное распределение имеет на графике распределения две вершины, даже если частоты для двух вершин не строго равны. В последнем случае выделяют большую и меньшую моду. Во всей группе может быть и несколько локальных вершин распределения частот. Тогда выделяют наибольшую моду и локальные моды.

Еще раз отметим, что мода − это значение признака, а не его частота.

Медиана (Md) − это такое значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая − больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:

а) если данные содержат нечетное число значений (8, 9, 10, 13, 15), то ме­диана есть центральное значение, т. е. Md = 10;

б) если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Мd = (8 + 9) : 2 = 8,5.

Среднее (М_х или 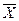− выборочное среднее, среднее арифметическое) − определяется как сумма всех значений измеренного признака, деленная на количество суммированных значений.

Если некоторый признак X измерен в группе испытуемых численностью N, мы получим значения: х₁ х₂, ..., х_i, ..., x_N (где i − текущий номер испытуе­мого, от 1 до N). Тогда среднее значение М_х или 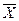определяется по формуле:

.

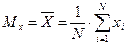Свойства среднего. Если к каждому значению переменной прибавить одно и то же число с, то среднее увеличится на это число (уменьшится на это число, если оно отрицательное):

.

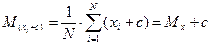А если каждое значение переменной умножить на одно и то же число с, то среднее увеличится в с раз (уменьшится в с раз, если делить на с):

.

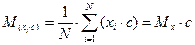Далее мы неоднократно будем обращаться к такой величине, как отклонение от среднего: (х_i – М_х). Из первого, очевидного свойства среднего следует еще одно важное свойство, не столь очевидное: сумма всех отклонений от среднего равна нулю:

.

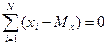Соответственно, среднее отклонение от среднего также равно 0.