Уравнения движения жидкости

При установившемся движении жидкости произведение площади живого сечения на среднюю скорость потока является постоянной величиной:

Q = S₁∙n₁ = S₂∙n₂ = S₃∙n₃ … = S_n∙n_n = const (1.31)

и называется уравнением неразрывности (расхода) потока.

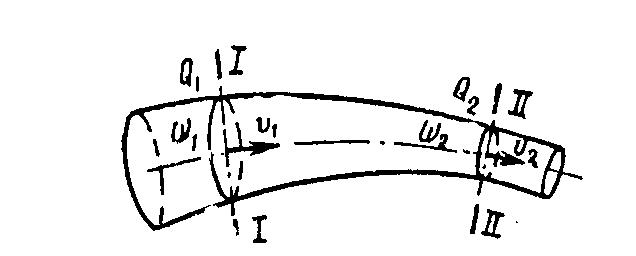
Рассматривая два сечения потока и учтя, что по закону сохранения энергии суммарная энергия, внесенная через сечение I-I при установившемся движении должна быть равна суммарной энергии, вынесенной через сечение II-II, рис. 1.8, можно записать следующее равенство:

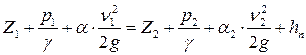. (1.32)

Это так называемое уравнение Бернулли.

Здесь: Z – высота расположения центра тяжести сечения над произвольно выбранной горизонтальной плоскостью (плоскостью сравнения);

р – давление (абсолютное или избыточное) в центре тяжести сечения;

n - средняя скорость, ;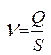

α – коэффициент кинетической энергии потока, безразмерная величина, зависящая от распределения скоростей по сечению потока;

h_п – потери напора на местные сопротивления, потери на трение.

Слагаемые трехчленов левой и правой частей уравнения Бернулли характеризуют: Z – геометрический напор, 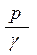- пьезометрический напор, 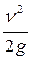- скоростной напор.

Рис. 1.8 – Схема к выводу уравнения неразрывности потока

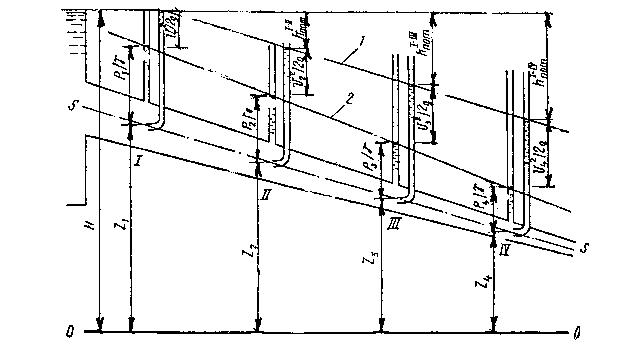
Если в каком-либо сечении потока жидкости, рис. 1.9, установить две трубки - пьезометрическую 1 и скоростную 2, то в скоростной трубке создается дополнительное давление от воздействия скорости движущейся жидкости и высота подъема жидкости в ней больше, чем в пьезометрической на величину 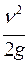. Линия, соединяющая уровни в пьезометрических трубках, называется пьезометрической линией. Линия, соединяющая уровни в скоростных трубках, называется напорной линией.

Рассмотрим равномерное движение жидкости в трубе. Сила трения по всей поверхности участка трубы длиной l определяется как:

Т = t₀× 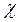×l, (1.33)

где t₀ – сила трения на единице площади поверхности потока со стенкой трубы.

В единицу времени эта сила производит работу:

Т×n = t₀× 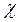×l×n. (1.34)

Рис. 1.9 – Графическое изображение членов уравнения Бернулли 1 – напорная линия (линия суммарной удельной энергии); 2 - пьезометрическая линия (линия потенциальной удельной энергии); 3 – линия плоскости сравнения

С другой стороны, работа сил трения на поверхности соприкосновения равна энергии, затрачиваемой потоком на преодоление трения на рассматриваемом участке:

Э = h_l×g×S×n. (1.35)

Приравняв правые части уравнений (1.33) и (1.35), получим:

t₀× 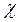×l = h_l×g×S×n или 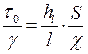, (1.36)

но 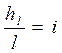есть гидравлический уклон, а 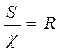- гидравлический радиус, откуда:

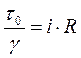. (1.37)

Полученное уравнение является основным уравнением равномерного движения жидкости.