Физические свойства жидкостей

Жидкость характеризуется малым сцеплением между частицами, вследствие чего обладает текучестью и принимает форму сосуда, в который ее поместили.

Различают капельные и газообразные жидкости. Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы), малым сопротивлением растягивающим усилиям и малым трением между частицами. Газообразные жидкости характеризуются практически полным отсутствием сопротивления сжатию.

К капельным жидкостям относятся: вода, нефть, нефтепродукты (бензин, керосин и др.), к газообразным - все газы.

Основные физические свойства жидкости: удельный вес, плотность, сжимаемость, температурное расширение, вязкость.

Удельный вес жидкости:

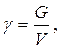G = m∙g, (1.1)

где G – вес жидкости объемом V.

Плотность жидкости:

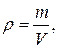(1.2)

где m – масса жидкости в объеме V.

Сжимаемость жидкости, характеризуется коэффициентом объемного сжатия:

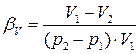, (1.3)

где V₁ и V₂ – начальный и конечный объемы жидкости;

р₁ и р₂ – начальное и конечное давления на единицу объема жидкости.

В диапазоне давлений от 0,1 до 50 МПа коэффициент b_v практически остается неизменным.

Величина, обратная коэффициенту сжимаемости, называется модулем упругости жидкости:

Е₀ = 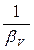. (1.4)

Температурное расширение жидкости характеризуется коэффициентом температурного расширения b_t:

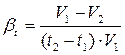, (1.5)

где t₁ и t₂ – начальная и конечная температуры жидкости.

Следует отметить, что объем воды при ее нагревании от 0 до 4°С уменьшается и при +4°С плотность воды максимальна, при дальнейшем нагревании объем воды увеличивается.

Вязкость жидкости – это ее свойство оказывать сопротивление относительному сдвигу частиц, обусловленное силами внутреннего трения между слоями жидкости.

Сила внутреннего трения между частицами жидкости определяется как:

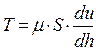, (1.6)

где S – площадь поверхности соприкасающихся слоев;

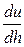- градиент скорости перемещения слоев;

h – расстояние между слоями;

m - коэффициент внутреннего трения.

Коэффициент внутреннего трения определяет динамическую вязкость и находится как:

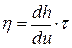, (1.7)

где t - касательные напряжения на поверхности слоев.

В системе СИ единицу динамической вязкости определяют как:

.

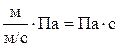В практических задачах используют понятие кинематической вязкости n :

n = 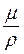. (1.8)

В системе СИ n имеет размерность:

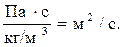
Гидростатика

Гидростатика изучает законы равновесия покоящейся жидкости. На покоящуюся жидкость действуют два вида сил: массовые (сила тяжести, сила инерции) и поверхностные (силы давления, центробежные силы).

Под действием внешних сил в каждой точке жидкости возникают внутренние силы, характеризующие ее напряженное состояние. Предел отношения равнодействующей внешних сил к элементарной площадке называют гидростатическим давлением:

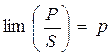. (1.9)

Гидростатическое давление обладает двумя свойствами: первое – оно всегда направлено по нормали к площадке, второе – в любой точке жидкости оно всегда одинаково по всем направлениям.

Если покоящаяся жидкость находится под действием только силы тяжести, то дифференциальное уравнение равновесия запишется как:

g∙dz = 0.

Интегрируя получим z = const, т.е. свободная поверхность есть горизонтальная плоскость, рис 1.1 а.

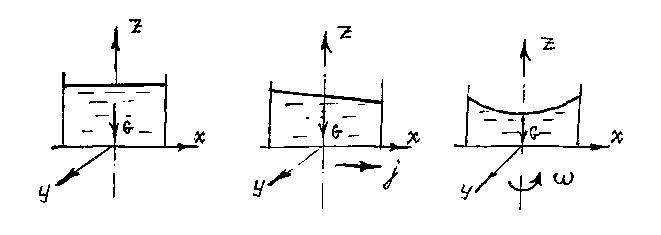
Рис. 1.1 - Формы свободной поверхности под действием силовых факторов: а – воздействие силы тяжести; б - воздействие силы тяжести и сил инерции; в - воздействие силы тяжести и угловой скорости.

Если жидкость заключена в сосуде, движущемся прямолинейно с постоянным ускорением j, то она находится в относительном покое (т.е. не перемещается относительно сосуда) и дифференциальное уравнение равновесия имеет вид:

- jdx + gdz = 0, (1.10)

откуда после интегрирования получим уравнение наклонной плоскости:

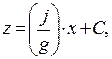(1.11)

т.е. поверхность жидкости, находящейся под действием силы тяжести и силы инерции наклонена к горизонту под углом α (рис.1.1б):

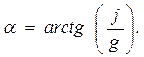(1.12)

Если жидкость заключена в сосуде, который вращается вокруг вертикальной оси с постоянной угловой скоростью ω, то она находится в относительном покое и уравнение равновесия опишется как:

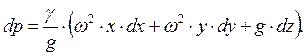(1.13)

Интегрируя, получим:

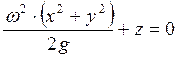или 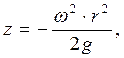(1.14)

т.е. свободная поверхность жидкости приобретает вид параболоида вращения, рис. 1.1 в.

Рассмотрим жидкость, находящуюся в покое и определим гидростатическое давление Р в точке А на элементарной площадке S, расположенной на глубине h от свободной поверхности и параллельной ей, рис. 1.2.

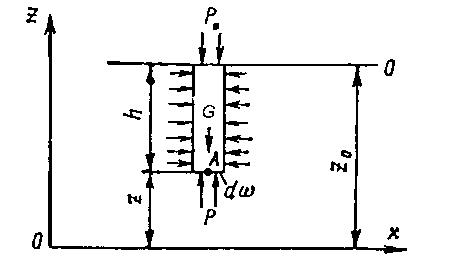
Рис. 1.2 – Схема к выводу основного уравнения гидростатики

Сумма проекций всех сил на ось Z:

р∙dS - g∙h dS – р₀ dS = 0 или р = р₀ + g∙h, (1.15)

т.е. давление, приложенное к свободной поверхности жидкости, передается во все точки жидкости без изменения, это положение называется законом Паскаля.

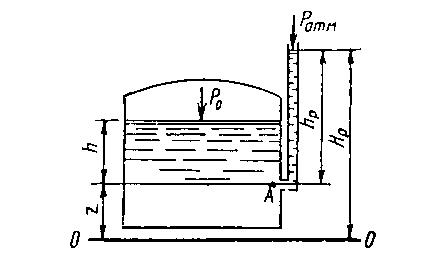
Рассмотрим жидкость, находящуюся в сосуде под давлением Р₀ и сообщающуюся с атмосферой, рис. 1.3. Абсолютное давление или полное гидростатическое давление в точке А состоит из:

р_абс = р_атм + g×h_р, (1.16)

а с другой стороны:

р_абс = р₀ + g×h, (1.17)

откуда:

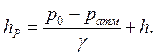(1.18)

Величина h_P называется пьезометрической высотой.

Высоту поднятия жидкости в трубке (пьезометре) относительно плоскости отсчета называют пьезометрическим напором.

Для закрытого сосуда;

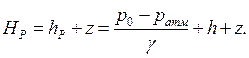(1.19)

Рис. 1.3 – Схема установки пьезометра

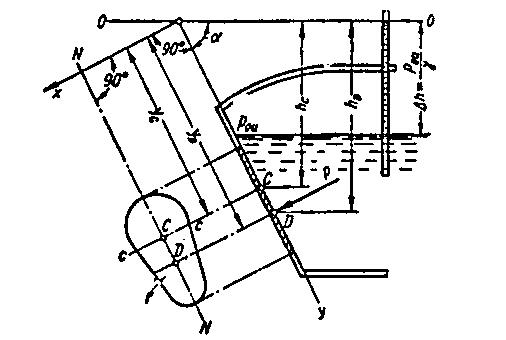
Определим силы давления покоящейся жидкости на стенку сосуда. Рассмотрим случай давления на плоскую стенку, рис. 1.4.

Рис. 1.4 – Схема к определению сил давления покоящейся жидкости на плоскую стенку сосуда

Если плоская стенка подвергается одностороннему давлению жидкости (на несмоченной стороне стенки – атмосферное давление), то полная сила давления Р воспринимая стенкой и нормальная к ней:

Р = р_с∙F = g∙h_c∙F, (1.20)

где F – смоченная площадь стенки;

р_с – избыточное давление в центре тяжести площади F;

h_c – расстояние по вертикали от центра тяжести площади F до пьезометрической плоскости или плоскости напора 0-0.

Положение центра давления (точка D) определяется формулой:

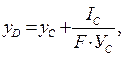(1.21)

где y_D и y_С – расстояния центра давления D и центра тяжести С стенки до линии пересечения плоскости стенки с пьезометрической плоскостью;

I_C – момент инерции площади стенки относительно оси С-С, проходящей через центр тяжести С.

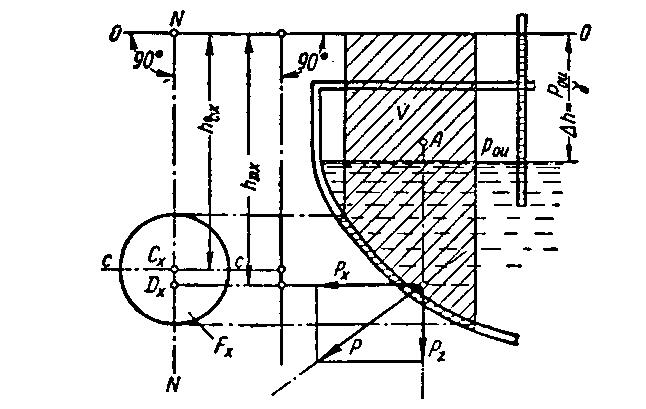
Рис. 1.5 – Схема к определению сил давления покоящейся жидкости на криволинейную стенку сосуда

Формулу (1.21) можно привести к виду:

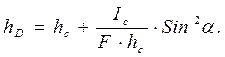(1.22)

Для вертикальной стенки:

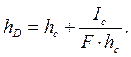(1.23)

Для криволинейной стенки полная сила Р находится в плоскости, нормальной к образующей, рис.1.5

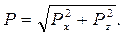(1.24)

Горизонтальная составляющая:

Р_х = F_x∙p_cx, (1.25)

где F_x – площадь проекции криволинейной стенки на вертикальную плоскость,

p_cx = g∙h_cx – избыточное давление жидкости на уровне центра тяжести этой жидкости.

Вертикальная составляющая:

P_z = V∙g, (1.26)

где V – объем, ограниченный стенкой, вертикальным проектирующим цилиндром и пьезометрической плоскостью.

Положение линий действия горизонтальной составляющей (координаты h_DX) определяется как для вертикальной стенки.

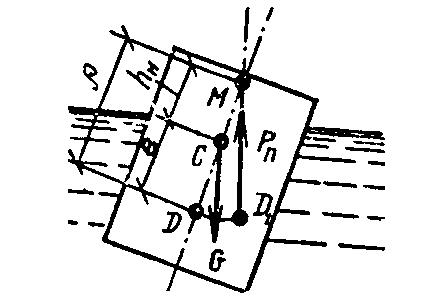
Результирующая сила давления жидкости на поверхность, погруженного в нее тела равна весу жидкости в объеме погруженной части тела и направлена вверх по вертикали – закон Архимеда:

P= V_Т∙g, (1.27)

где V_Т – объем жидкости, вытесненной телом.

Линия действия выталкивающей силы проходит через центр тяжести вытесненного объема жидкости и называется центром водоизмещения, рис. 1.6. В общем случае центр водоизмещения (точка D) не совпадает с центром тяжести тела (точка С).

Рис. 1.6 – Схема действия сил на тело, погруженное в жидкость

Устойчивость тела при подводном плавании достигается при расположении его центра тяжести ниже центра водоизмещения D.

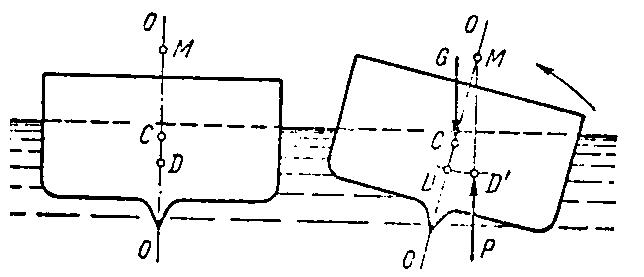
Надводное плавание устойчиво, если метацентр М находится выше центра тяжести С. Метацентр – точка пересечения линии действия подъемной силы Р, действующей на выведенное из равновесия плавающее тело с осью симметрии тела 0-0.

Остойчивость – это способность плавающего тела сохранять устойчивое равновесие при кренах. Мерой остойчивости служит метацентрическая высота МС. Чем больше высота МС, тем выше остойчивость, рис. 1.7.

Рис. 1.7 – Схема к определению остойчивости плавающего тела

Гидродинамика

Параметры, характеризующие движение жидкости: скорость и давление.

Задачей гидродинамики является исследование законов изменения этих параметров во времени и в пространстве, т.е. нахождение функций:

(1.28)

U = f₁([x, y, z, t),

p = f₂[x, y, z, t).

Здесь: U и p – скорость и давление в рассматриваемой точке жидкости;

x, y, z – координаты точек;

t – время.

Установившееся движение жидкости имеет место, когда скорость потока и давление в любой его точке не изменяются во времени. Пример – истечение жидкости из отверстия в сосуде при постоянном напоре.

Неустановившееся движение жидкости имеет место, когда скорость движения и давление в каждой точке изменяются с течением времени. Пример – истечение жидкости из отверстия в сосуде при переменном напоре.

Потоком жидкости называют совокупность элементарных струек, представляющую собой непрерывную массу движущихся в каком-либо направлении.

Живым сечением потока S называют поперечное сечение потока, перпендикулярное его направлению.

Расходом потока Q называется объем жидкости, проходящий в единицу времени через живое сечение потока. Измеряется в м³/с, л/с.

Смоченным периметром 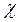называют часть периметра живого сечения, на которой жидкость соприкасается с твердыми стенками.

Гидравлическим радиусом R называется отношение площади живого сечения потока к смоченному периметру:

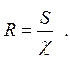(1.29)

Средней скоростью потока n называется частное от деления расхода потока на площадь его живого сечения:

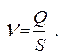(1.30)

Равномерным называется такое установившееся движение жидкости, при котором живое сечение и средняя скорость потока не меняются по длине. Пример – движение жидкости в цилиндрической трубе.

Неравномерным называется такое установившееся движение жидкости, при котором живое сечение и средняя скорость потока изменяются по его длине. Пример – движение жидкости в конической трубе.

Напорным называется поток, у которого по всему периметру живого сечения жидкость соприкасается с твердыми стенками. Пример – движение воды в трубах.

Безнапорным называется поток со свободной поверхностью. Пример – движение воды в реках, канализационных трубах.