Режимы движения жидкости

Режим движения жидкости может быть двух видов: ламинарным (параллельно струйчатым) и турбулентным (беспорядочным).

Впервые это отметил в 1880 г. Менделеев, а в 1883 г. экспериментально подтвердил Рейнольдс.

Критерием, определяющим вид (режим) движения служит безразмерный параметр Re (число Рейнольдса):

,

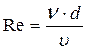где u - кинематическая вязкость.

Критическая величина параметра Re, при которой ламинарный поток переходит в турбулентный Re = 2320.

При безнапорном движении жидкости число Re определяется по формуле:

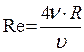, (1.43)

где R – гидравлический радиус.

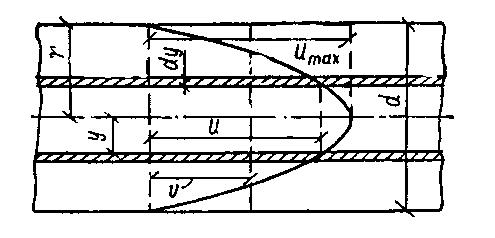
Закон распределения скоростей по живому сечению потока при ламинарном режиме в трубопроводе описывается формулой Стокса:

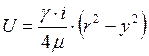, (1.44)

где U – скорость движения слоя жидкости;

y – расстояние слоя от оси трубопровода;

i – гидравлический уклон;

r – радиус трубы, r = d/2;

m - динамическая вязкость.

На рис. 1.10 показано распределение скоростей в потоке при ламинарном режиме. Оно будет параболическим и максимальная скорость определяется как:

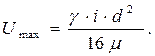(1.45)

Рис. 1.10 – Распределение скоростей по сечению потока в трубопроводе при ламинарном движении жидкости

Средняя скорость потока определяется как:

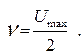(1.46)

При турбулентном режиме скорость движения в каждой точке потока изменяется по величине и направлению и колеблется в пределах некоторого среднего значения, называемого местной скоростью. Местные скорости по сечению потока практически постоянны и направлены вдоль оси потока, по этому условию при турбулентном режиме поток можно рассматривать как струйный с определенной скоростью и к нему применимо уравнение Бернулли.

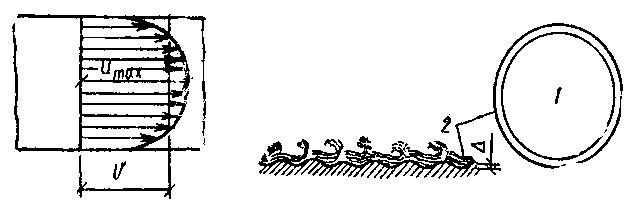
Прандлем была предложена модель турбулентного движения потока жидкости в виде тонкого ламинарного слоя по периметру трубы и турбулентного ядра в центре, рис. 1.11.

Рис. 1.11 – Распределение скоростей по сечению потока в трубопроводе при турбулентном движении жидкости: 1 – турбулентное ядро; 2 – ламинарный слой

Альтштулем А. и Калицуном В. была предложена зависимость, описывающая распределение скоростей по сечению потока при турбулентном режиме движения жидкости в трубе:

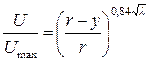, (1.47)

где l - коэффициент гидравлического трения.

Различают три области определения коэффициента гидравлического трения: область гидравлически гладких труб (малые значения числа Re), область шероховатого трения (область квадратичного сопротивления, соответствует большим числам Re), переходная область между первой и второй.

Для области гидравлически гладких труб l определяется по формуле Блазиуса:

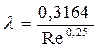. (1.48)

Для области квадратичного сопротивления l определяется по формуле Шифринсона:

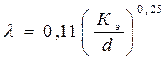, (1.49)

где К_э – эквивалентная шероховатость в мм (справочная величина, зависящая от материала стенки труб и условий их эксплуатации).

Следует отметить, что в практических расчетах используются и другие формулы для определения l.