Критерии оптимальности
Пусть ЛПР может выбрать один из п возможных вариантов своих решений X1,X2,…,Xn и пусть относительно условий , в которых будут реализованы возможные варианты, можно сделать т предположений Y1,Y2,…,Y m.Оценки сочетания каждого варианта решения в каждыхусловиях (Xi ,Yi) известны и заданы в виде некоторой матрицы
выигрышей 







 лица, принимающего решения.
лица, принимающего решения.

Априорная информация о вероятностях возникновения той или иной ситуации Yj может быть известна (т.е. достаточно просто определима на основании эмпирического опыта или экспертных оценок) или отсутствует (все ситуации рассматриваются как равновероятные).

Теория статистических решений предлагает несколько критериев оптимальности выбора решений. Выбор того или иного критерия неформализуем, он осуществляется человеком, принимающим решения, субъективно, исходя из его опыта, интуиции и т.п. Однако существуют определенные рекомендации по выбору критериев оценки, в наибольшей степени соответствующие оцениваемой проблеме. Рассмотрим эти критерии и рекомендации по их использованию.
Критерий Лапласа.
Критерий Лапласа является критерием среднего выигрыша, когда не учитывается априорная информация и предполагается
равновероятность объективных условий. Поскольку вероятности возникновения той или иной ситуации Yj неизвестны, будем их все
считать равновероятными: 






 . Тогда для каждой строки матрицы
. Тогда для каждой строки матрицы

выигрышей подсчитывается среднее арифметическое значение оценок. Решение принимается по максимуму среднего ожидаемого значения оценок эффективности по всем состояниям обстановки, т.е. оптимальному решению будет соответствовать такое решение, которому соответствует максимальное значение этого среднего арифметического:

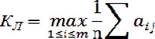


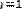
Применение данного критерия оправданно, если ситуация, в которой принимается решение, характеризуется следующими признаками:

ü вероятности появления состояния неизвестны, не зависят от времени и равны;
ü решение реализуется большое (теоретически бесконечное) число раз;
ü для небольшого числа реализаций допускается некоторый
неоцениваемый риск.
Критерий Байеса–Лапласа. Данный критерий рассматриваетсятакже как критерий среднего выигрыша, но используется в ситуациях для которых известна вероятность pj осуществления того или иного состояния среды Yj. С учетом данной вероятности рассчитывается
математическое ожидание результата ЛПР по каждой из строк: 





 . Оптимальными определяются варианты, которые соответствуют максимальному значению рассчитанных математических ожиданий:
. Оптимальными определяются варианты, которые соответствуют максимальному значению рассчитанных математических ожиданий:


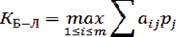


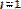
Применение данного критерия целесообразно, если ситуация, в которой принимается решение, характеризуется следующими признаками:

ü вероятности появления состояния известны ( либо достаточно легко определимы или рассчитаны) и не зависят от времени;
ü решение реализуется большое (теоретически бесконечное) число раз;
ü для небольшого числа реализаций допускается некоторый неоцениваемый риск.
При достаточно большом количестве реализаций среднее значение постепенно стабилизируется, поэтому при полной (бесконечной) реализации решения какой-либо риск практически исключен. Таким образом, критерий Байеса—Лапласа может дать хороший результат, однако он предполагает большую информированность ЛПР и достаточно длительную реализацию.
Критерий Вальда (максимина).
Критерий является критерием «крайнего пессимизма» и
ориентирован на выбор наилучшего действия при самых неблагоприятных условиях. Из каждой строки i выбираются минимальные элементы, т.е. значения, которые соответствуют наихудшему результату действий ЛПР при известных состояниях «природы» Yj , и в результате выбирается стратегия, соответствующая максимальному элементу из отобранных минимальных:
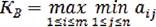
Выбранные таким образом варианты полностью исключают риск, поскольку ЛПР не может столкнуться с худшим результатом, чем тот, на который он ориентируется.

Применение данного критерия оправданно, если ситуация, в которой принимается решение, характеризуется следующими признаками:
ü вероятности состояний «природы» неизвестны;
ü необходимо считаться с наихудшим из возможных вариантов;
ü решение реализуется только один раз или очень малое количество раз;
ü риск полностью недопустим.
Таким образом, с позиций максиминного критерия Вальда выбирается стратегия, отвечающая лучшему из самых неудачных результатов. Этот критерий очень осторожен. Он ориентирован на наихудшие условия, только среди которых и отыскивается наилучший,
и теперь уже гарантированный результат.
Критерий Сэвиджа.
Сущность этого критерия заключается в минимизации риска. Как
и критерий Вальда, критерий Сэвиджа очень осторожен, но отличается от критерия Вальда другим пониманием худшей ситуации. Для критерия Вальда – это минимальный выигрыш, для критерия Сэвиджа – максимальная потеря выигрыша по сравнению с тем, чего можно было бы достичь в данных условиях.
Расчет данных для использования критерия производится в следующем порядке. На первом этапе в каждом столбце матрицы находится максимальная оценка 








 и составляется новая
и составляется новая

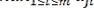
матрица (матрица рисков 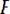








 ),элементы которой определяютсясоотношением:
),элементы которой определяютсясоотношением:

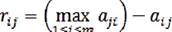
Величину rij называют риском (потерей), под которым понимают разность между максимальным выигрышем, который имел бы место, если бы было достоверно известно, что наступит ситуация Yj, и выигрышем при выборе решения Xi в условиях Yj.

На втором этапе из матрицы рисков выбирают такое решение, при котором величина риска принимает наименьшее значение в самой неблагоприятной ситуации:
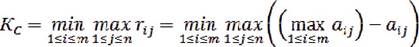
Критерий Сэвиджа предпочтителен в тех же ситуациях, в которых используется критерий Вальда.
 Критерий Гурвица.
Критерий Гурвица.
Этот критерий обеспечивает промежуточное решение между крайним оптимизмом и крайним пессимизмом.
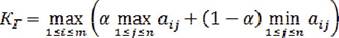
Для проведения расчетов необходимо ввести некоторый коэффициент , называемый коэффициентом оптимизма. При α=0 критерий Гурвица превращается в пессимистический критерий Вальда. Это случай ”крайнего пессимизма”. При α=1 он превращается в критерий «крайнего оптимизма » (критерий максимакса), т.е. отражает позицию ЛПР, ожидающего наиболее благоприятного стечения обстоятельств. Значения 






 характеризуют некоторое промежуточное отношение ЛПР к возможным рискам.
характеризуют некоторое промежуточное отношение ЛПР к возможным рискам.


Коэффициент оптимизма назначается субъективно, исходя из опыта, интуиции и т.п. Чем более опасна ситуация, тем более осторожным должен быть подход к выбору решения и тем меньшее значение присваивается коэффициенту . При нейтральной оценке риска возможно использование значения α = 1/2.
При выполнении расчетов в каждой строке матрицы выигрышей находится самая большая оценка 









 и самая маленькая
и самая маленькая


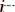









 . Они умножаются соответственно на и 1 , затем
. Они умножаются соответственно на и 1 , затем

вычисляется их сумма. Оптимальному решению будет соответствовать такое решение, которому соответствует максимум этой суммы:
 Применение критерия Гурвица оправданно, если ситуация, в которой принимается решение, характеризуется следующими признаками:
Применение критерия Гурвица оправданно, если ситуация, в которой принимается решение, характеризуется следующими признаками:
ü вероятности состояний «природы» неизвестны;
ü необходимо считаться с наихудшим из возможных вариантов;
ü реализуется малое количество решений;
ü допускается некоторый незначительный риск.
Дата добавления: 2021-11-16; просмотров: 468;











