Вопрос№2,15. Динамические характеристики исполнительного механизма постоянной скорости
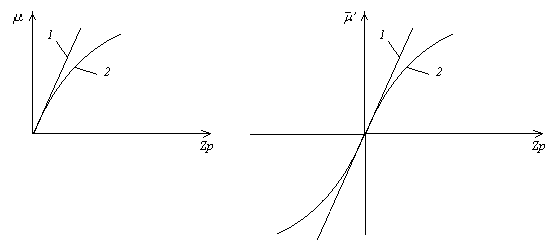
Исполнительный мембранный механизм может быть представлен как звено с нелинейной статической характеристикой (рис.7, а). Его характеристика находится в прямой зависимости от площади мембраны и в обратной – от коэффициента жесткости пружины (возрастающей по мере ее сжатия). Соответственно, при малых изменениях 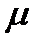 динамическую характеристику мембранного исполнительного механизма можно представить пропорциональным звеном
динамическую характеристику мембранного исполнительного механизма можно представить пропорциональным звеном
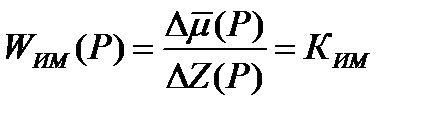 , (1)
, (1)
причем коэффициент передачи 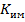 несколько убывает с ростом
несколько убывает с ростом 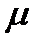 .
.
а б
Рис.7. Статические характеристики мембранного (а)
и гидравлического (б) исполнительных механизмов:
1 – идеальная; 2 – реальная
Гидравлический исполнительный механизм может рассматриваться как звено с нелинейной статической характеристикой (рис.7, б). Это связано с возрастанием постоянной интегрирования реального исполнительного механизма при больших скоростях перемещения поршня (за счет резкого увеличения сил вязкого трения).
Динамика гидравлического исполнительного механизма при малых входных воздействиях может быть представлена линейным интегрирующим звеном
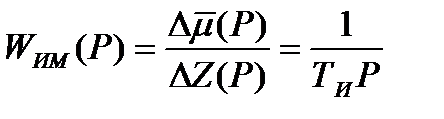 . (2)
. (2)
Исполнительный механизм постоянной скорости может находиться только в трех установившихся состояниях: вращение ротора с постоянной скоростью S, неподвижность, вращение с той же скоростью в противоположную сторону. Статическая характеристика исполнительного механизма постоянной скорости представлена на рис.8.
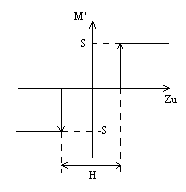
Рис.8. Статическая характеристика исполнительного механизма
постоянной скорости
При превышении сигнала управления Zu половины зоны нечувствительности H/2 происходит включение электродвигателя, который начинает перемещать с постоянной скоростью S вал исполнительного механизма.
Пусть на вход исполнительного механизма постоянной скорости поступает импульсный управляющий сигнал (рис.9, а) с амплитудой (0, А), при этом носителем информации является скважность импульсов g, поступающих с периодом Т=Dtи+Dtп:
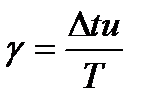 , (3)
, (3)
где Dtи – время импульса; Dtп – время паузы.
Тогда реакция исполнительного механизма постоянной скорости на импульсное воздействие будет иметь вид, представленный на рис.9, б. Можно записать следующее равенство: 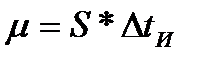 ,
, 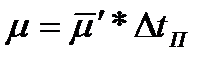 , тогда средняя скорость движения
, тогда средняя скорость движения 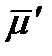 будет связана со скважностью следующим соотношением:
будет связана со скважностью следующим соотношением:
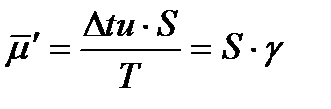 . (4)
. (4)
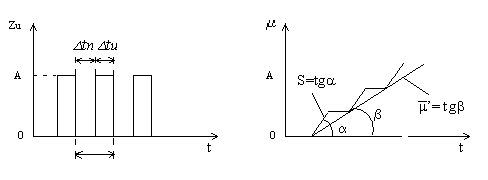
а б
Рис.9. Динамическая характеристика исполнительного механизма
постоянной скорости
Таким образом, по отношению к скважности импульсного сигнала исполнительный механизм постоянной скорости ведет себя в среднем как интегрирующее звено, и его передаточную функцию можно представить в следующем виде:
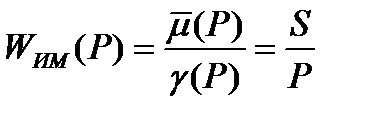 . (5)
. (5)
Если принять перемещение исполнительного механизма от 0 до 1, тогда скорость запишется как
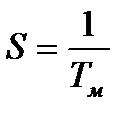 , (6)
, (6)
Тм – время полного хода ИМ, с.
Тогда передаточная функция ИМ примет следующий вид
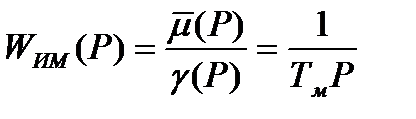
Дата добавления: 2021-11-16; просмотров: 587;











