Периодическая система элементов Д.И. Менделеева
& Литература: [1], [3], [8], [6].
Периодическая система элементов была создана Д. И. Менделеевым задолго до появления квантовой механики чисто эмпирическим путем. Эта таблица наглядно отображает периодическую зависимость химических свойств элементов от заряда ядра атомов.
Квантовая механика дает теоретическое обоснование свойств элементов, исходя из строения атомов, объясняет, в частности, и периодическое изменение химических свойств с ростом порядкового номера элемента в таблице.
Порядковый номер элемента в таблице Менделеева совпадает с числом элементарных зарядов ядра. Столько же электронов входит в состав нейтрального атома этого элемента.
Считается, что каждый электрон атома движется в эффективном центральном поле, образованном ядром и остальными электронами. Поэтому его состояние характеризуется квантовыми числами n, l, и m. Д. Хартри и В. А. Фок разработали метод самосогласованного поля, позволяющий рассчитать энергетические уровни и волновые функции одно-частичных состояний электронов в атоме.
Идея метода самосогласованного поля заключается в следующем. Вначале задается выражение потенциальной энергии, грубо описывающее эффективное поле, в котором движется каждый электрон. С этим выражением вычисляются волновые функции, описывающие состояния электронов в атоме. Они позволяют уточнить вид эффективного поля и найти для него новые волновые функции. Повторяя эту процедуру последовательно несколько раз, можно решить задачу достаточно точно.
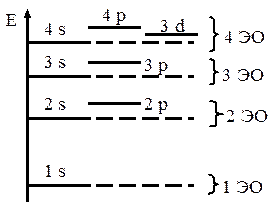 Рис. 30.1
Рис. 30.1
|
Вычисления приводят к схеме энергетических уровней одно-частичных состояний, изображенной на рис. 30.1 без соблюдения масштаба. Существенной особенностью этой схемы является то, что группы сравнительно близко расположенных уровней разделены значительными энергетическими интервалами. Каждую такую группу, а также совокупность относящихся к ней состояний электронов называют энергетической оболочкой (ЭО). На рис. 30.1 изображены четыре нижние энергетические оболочки. В первых трех оболочках большим числам n и l соответствуют более высокие уровни. В четвертой энергетической оболочке уровень 3d ниже, чем 4p, но выше, чем уровень 4s.
Для определения того, какой уровень выше, можно использовать эмпирические правила В.М. Клечковского: 1) тот уровень выше, для которого больше n + l; 2) при равных n + l выше уровень с большим n.
Энергия атома зависит от распределения электронов по одно-частичным состояниям, то есть от электронной конфигурации. Представляет интерес электронная конфигурация основного состояния атома. Она должна обеспечть наименьшее значение энергии атома без нарушения запрета Паули.
Число подлежащих заполнению состояний на каждом уровне зависит от квантовых чисел n, l, и m.
Совокупность состояний, соответствующих фиксированному квантовому числу n, называют слоем. Слои с n = 1, 2, 3, 4,… принято называть, соответственно, K, L, M, N,… -слоями.
Совокупность состояний с фиксированными числами n и l называют электронной оболочкой (подслоем). Не путайте электронную оболочку с энергетической оболочкой. Если n = 2 и l = 0, то используют название «2s-оболочка». Если n = 3 и l = 1, то говорят: «3p-оболочка». Аналогичным образом именуют и другие оболочки.
Фиксированному значению орбитального квантового числа l соответствуют 2l + 1 состояния с различными числами m. Эти состояния отличаются проекциями орбитального момента импульса. Учитывая две возможные ориентации спина (s = ±1/2), число подлежащих заполнению состояний оболочки с квантовым числом l оказывается равным 2 (2l + 1). В результате получается, что в n-м слое может разместиться число электронов,
равное 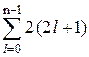 = 2 n2 . (30.1)
= 2 n2 . (30.1)
Зная энергетическую схему одно-частичных состояний и число состояний для каждого энергетического уровня, нетрудно установить электронную конфигурацию атомов. Рассмотрим некоторые примеры. Они отражены в приведенной ниже таблице.
В ячейках таблицы указано число электронов, находящихся в каждой электронной оболочке.
В полностью заполненной энергетической оболочке нет места для электронов другого атома, а размещение такого электрона на вышележащих свободных уровнях энергетически не выгодно. Не выгоден также уход электрона с полностью заполненной энергетической оболочки поскольку наименьшей энергией обладает система электронов с нулевым спином (все электроны «спарены»). Вот почему атомы с полностью заполненными энергетическими оболочками относятся к инертным газам. В приведенной таблице таковыми являются атомы He, Ne, Ar, Kr.
У атомов H, Li, Na, Ka в s-ом подслое почти пустой энергетической оболочки находится единственный электрон. Энергия связи его с атомом мала. Поэтому названные атомы активно вступают в химическую реакцию с теми, у которых энергетические оболочки почти заполнены, например, со фтором F или с хлором Cl. Электронная конфигурация верхней энергетической оболочки у фтора 2s22p5, а у хлора – 3s23p5. В обоих случаях до полного заполнения и уменьшения энергии при «спаривании» не хватает одного электрона.
Для характеристики электронной конфигурации атома в целом достаточно указать лишь электронную конфигурацию верхней энергетической оболочки, что обычно и делается, в том числе и в последней колонке приведенной таблицы. Чтобы получить полную электронную конфигурацию, следует слева приписать конфигурации предшествующих инертных газов.
Химические свойства атома определяются верхней, частично заполненной энергетической оболочкой. В реакциях в первую очередь участвуют наиболее далекие от ядра (валентные) электроны, для которых достаточно велико радиальное квантовое число nr= n – l – 1. Валентные электроны находятся в s- и p- оболочках (l = 0 и l = 1). Их число не превышает восьми
(2 + 6).
| Заряд ядра (в элем. заряах) | Элемент | Слои | Энергетичес-кие оболочки | Электронные конфигурации | |||||||
| K | L | M | N | ||||||||
| Оболочки | |||||||||||
| 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | ||||
| H | 1 ЭО | 1s1 | |||||||||
| He | 1s2 | ||||||||||
| Li | 2 ЭО | 2s1 | |||||||||
| Ne | 2s22p6 | ||||||||||
| Na | 3 ЭО | 3s1 | |||||||||
| Ar | 3s23p6 | ||||||||||
| K | – | 4 Э О | 4s1 | ||||||||
| Ca | – | 4s2 | |||||||||
| Sc | 3d14s2 | ||||||||||
| Ti | 3d24s2 | ||||||||||
| V | 3d34s2 | ||||||||||
| Zn | 3d104s2 | ||||||||||
| Ga | 3d104s24p1 | ||||||||||
| Kr | 3d104s24p6 |
Анализируя заполнение оболочек при последовательном переходе к атомам с все большим числом электронов, можно заметить изменение порядка заполнения, начиная с четвертой энергетической оболочки. Вслед за оболочкой 3p, заполнение которой завершается в атоме Ar, заполняется 4s-оболочка следующего слоя (K, Ca), хотя 3d-подслой имеет 10 свободных состояний. Лишь после Ca происходит заполнение вакантных состояний 3d-оболочки вплоть до Zn. Особенный порядок заполнения имеет место и у редкоземельных элементов (лантанидов). В атомах, начиная с лантана 57La и заканчивая лютецием Lu, происходит заполнение вакантных состояний 4f-оболочки 4-го слоя, в то время как число электронов, более удаленных от центра (оболочек 5s, 5p, 5d, 5f, 6s) остается неизменным. По этой причине химические свойства этих элементов так мало отличаются, что Д. И. Менделеев поместил все эти элементы в одну клетку своей таблицы. Аналогичная ситуация имеет место и для актинидов (элементов с порядковыми номерами от 89 до 103).
Поскольку химические свойства атомов определяются электронными конфигурациями верхних энергетических оболочек, то аналогичным электронным конфигурациям соответствуют близкие химические свойства. Это объясняет открытый Менделеевым закон периодичности свойств элементов. Например, электронные конфигурации у Be, Ma, Ca, соответственно, – 2s2, 3s2, и 4s2. Так что атомы этих элементов имеют по два валентных электрона в s-оболочках. По этой причине химические свойства указанных элементов сходны. Аналогичная ситуация имеет место и для других атомов, относящихся к одной группе таблицы Д.И. Менделеева.
В конце брошюры приведена современная форма таблицы Д.И. Менделеева, которая отличается от устаревшей, но еще не вышедшей из употребления короткой формы, в которой наряду с группами рассматриваются подгруппы элементов.
? Контрольные вопросы
1. Назовите принципы, лежащие в основе квантово-механического обоснования периодической системы Д. И. Менделеева.
2. Расскажите об энергетическом спектре одно-частичных состояний многоэлектронных атомов.
3. Расскажите об электронных слоях и оболочках.
4. Докажите равенство (30.1).
5. Расскажите о порядке заполнения электронных оболочек при последовательном переходе к атомам с все большим числом электронов.
6. В чем причина периодичности свойств химических элементов?
7. Запишите и объясните полную электронную конфигурацию конкретного атома (по указанию преподавателя).
8. Каковы химические свойства атомов, имеющих следующие электронные конфигурации: 2s22p4, 3s2 3p1, 3d54p1, 4d105s1?
Молекула водорода
& Литература: [1], [7], [8], [6].
Рассмотрение молекулы водорода позволяет понять природу химических связей, реализуемых в молекулах и в конденсированных средах.
Подобно атому гелия молекула водорода содержит два электрона, и поэтому ее волновая функция должна иметь спиновой сомножитель
Y(s1 s2), аналогичный спиновой части волновой функции атома гелия
(см. (29.4) – (29.7)). Имеется три спиновых состояния с суммарным спином
s = 1 (параллельные спины ↑↑), описываемые симметричными функциями (29.4) – (29.6), и одно состояние со спином s = 0 (антипараллельные спины ↑↓), описываемое симметричной функцией (29.7). Соответственно, координатная часть Y(1, 2) волновой функции молекулы водорода должна быть симметричной в случае антипараллельных спинов и антисимметричной, если спины параллельны:
Y(1, 2) = Ys(1, 2) = Y↑↓(1, 2) (32.1)
Y(1, 2) = Ya(1, 2) = Y↑↑(1, 2) (32.2)
Цифры 1 и 2 в качестве аргументов функции обозначают координаты первого и второго электрона.
Координатная часть волновой функции Y(1, 2) находится посредством решения стационарного уравнения Шредингера с таким гамильтонианом:  =
= 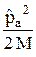 +
+ 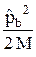 +
+ 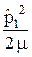 +
+ 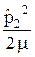 – e2k
– e2k 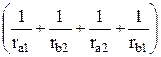 + e2k
+ e2k 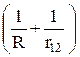 . (32.3)
. (32.3)
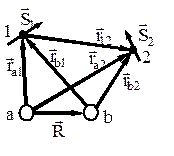 Рис. 32.1
Рис. 32.1
|
Здесь M – масса протона, m – масса электрона, k = 1 / (4 p e0). Смысл остальных величин ясен из рисунка 32.1.
При решении задачи используют так называемое адиабатическое приближение, основанное на малости массы электрона m по сравнению с массой протона M.
На первом этапе теории адиабатического приближения в выражении (32.3) пренебрегают величиной
 ab =
ab = 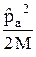 +
+ 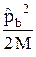 (32.4)
(32.4)
и решают стационарное уравнение Шредингера с оставшейся частью
 R(1, 2) гамильтониана:
R(1, 2) гамильтониана:  R(1, 2) YR(1, 2) = E(R) YR(1, 2). (32.5)
R(1, 2) YR(1, 2) = E(R) YR(1, 2). (32.5)
Физический смысл сделанного приближения заключается в пренебрежении движением ядер. Уравнение (32.5) описывает движение электронов в поле неподвижных ядер. Расстояние R между ядрами входит в (32.5) в качестве параметра.
В операторе  R(1, 2) целесообразно выделить следующие слагаемые:
R(1, 2) целесообразно выделить следующие слагаемые:
 R(1, 2) =
R(1, 2) =  a(1) +
a(1) +  b(2) +
b(2) + 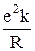 +
+ 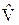 , (32.6)
, (32.6)
где  a(1) и
a(1) и  b(2) – гамильтонианы изолированных атомов водорода с ядрами a и b, а
b(2) – гамильтонианы изолированных атомов водорода с ядрами a и b, а 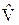 – оператор возмущения, описывающий взаимодействие электронов друг с другом и с «чужими» ядрами:
– оператор возмущения, описывающий взаимодействие электронов друг с другом и с «чужими» ядрами:
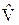 = e2 k
= e2 k 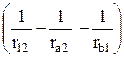 . (32.7)
. (32.7)
Тогда в нулевом приближении ( 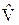 » 0) получается уравнение Шредингера с разделяющимися переменными. В результате приходим к заключению, что энергия E0(R) рассматриваемой системы в нулевом приближении является суммой энергий изолированных атомов Ea и Eb и кулоновской энергии взаимодействия ядер: E0(R) = Ea + Eb +
» 0) получается уравнение Шредингера с разделяющимися переменными. В результате приходим к заключению, что энергия E0(R) рассматриваемой системы в нулевом приближении является суммой энергий изолированных атомов Ea и Eb и кулоновской энергии взаимодействия ядер: E0(R) = Ea + Eb + 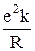 . (32.8)
. (32.8)
|
|
Здесь N±(R) – нормирующий множитель, Знак «+» соответствует антипараллельной ориентации спинов ↑↓, а знак «–» – параллельной ↑↑ (см. (32.1)
и (32.2)).
|
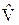 (32.7) снимает это вырождение. Для нахождения поправок DE, определяющих положение подуровней, целесообразно воспользоваться соотношением (26.10), аналогично тому, как это делалось в случае атома гелия. Получим:
(32.7) снимает это вырождение. Для нахождения поправок DE, определяющих положение подуровней, целесообразно воспользоваться соотношением (26.10), аналогично тому, как это делалось в случае атома гелия. Получим:
|
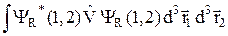 ÞDE = 2 N±2(R) (Q ± A) , (32.10)
ÞDE = 2 N±2(R) (Q ± A) , (32.10)
где Q = 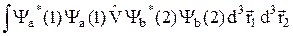 – (32.11)
– (32.11)
кулоновский интеграл, а
A = 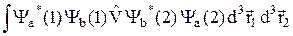 – (32.12)
– (32.12)
обменный интеграл.
 Структура формул (32.11) и (32.12) такая же, как и (29.21) и (29.22) для атома гелия. Следовательно, аналогичен и смысл описываемых ими величин Q и A. Отличие – в несколько ином виде оператора возмущения, а также в том, что в (32.12) предполагается переход электронов от одного атома к другому и наоборот, а в (29.22) – переход электронов одного и того же атома из одного состояния в другое.
Структура формул (32.11) и (32.12) такая же, как и (29.21) и (29.22) для атома гелия. Следовательно, аналогичен и смысл описываемых ими величин Q и A. Отличие – в несколько ином виде оператора возмущения, а также в том, что в (32.12) предполагается переход электронов от одного атома к другому и наоборот, а в (29.22) – переход электронов одного и того же атома из одного состояния в другое.
Складывая (32.8) и (32.10), получим энергию E(R) рассматриваемой системы при фиксированных расстояниях R между протонами. На рисунке 32.2 показан характер зависимости E(R) для обеих взаимных ориентаций электронных спинов.
При антипараллельной ориентации спинов энергия оказывается не только меньше из-за того, что A < 0 , но и имеет минимум в точке R = R0. Наличие этого минимума означает, что образуется связанная система с равновесным расстоянием R0 между центрами двух атомов водорода. Говорят, что атомы соединяются в молекулу водорода посредством ковалентной связи. При параллельной ориентации спинов связанная система не образуется. Возникновение ковалентной связи обусловлено величиной A, входящей в формулу (32.10). Эта величина отражает обменное взаимодействие, которое, оставаясь электромагнитным по своей природе, существенно зависит от взаимной ориентации спинов электронов.
 Парадоксальное на первый взгляд электрическое притяжение между нейтральными атомами водорода, проявляющееся при ковалентной связи, становится естественным, если проанализировать распределение электрического заряда в состояниях, описываемых формулой (32.9).
Парадоксальное на первый взгляд электрическое притяжение между нейтральными атомами водорода, проявляющееся при ковалентной связи, становится естественным, если проанализировать распределение электрического заряда в состояниях, описываемых формулой (32.9).
На рисунке 32.3 сплошными линиями изображены атомарные функции Ya и Yb в 1s-состояниях, а пунктиром – симметричная молекулярная функция Y↑↓, определяемя формулой (32.9). Благодаря знаку «+» в (32.9), функция Y↑↓ имеет максимум посредине между ядрами a и b. Здесь плотность отрицательных зарядов оказывается максимальной. Это и приводит к стягиванию положительных ядер a и b.
 Для параллельной ориентации спинов электронов в формуле (32.9) нужно брать знак «–». Тогда возникает ситуация, изображенная на рис. 32.4. Молекулярная функция Y↑↑ равна нулю посредине между ядрами. Отрицательные заряды главным образом оказываются локализованными с внешней стороны ядер. Они удаляют ядра друг от друга.
Для параллельной ориентации спинов электронов в формуле (32.9) нужно брать знак «–». Тогда возникает ситуация, изображенная на рис. 32.4. Молекулярная функция Y↑↑ равна нулю посредине между ядрами. Отрицательные заряды главным образом оказываются локализованными с внешней стороны ядер. Они удаляют ядра друг от друга.
Второй этап теории адиабатического приближения заключается в анализе движения ядер, для чего следует учесть отброшенную на первом этапе часть гамильтониана (32.4) при решении стационарного уравнения Шредингера:
{  R(1, 2) +
R(1, 2) +  ab(
ab( 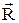 )} Y(1, 2,
)} Y(1, 2, 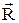 ) = E Y(1, 2,
) = E Y(1, 2, 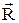 ) . (32.13)
) . (32.13)
Функция Y(1, 2, 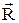 ), удовлетворяющая уравнению (32.13), описывает движение и электронов, и ядер. Ее представляют в виде произведения:
), удовлетворяющая уравнению (32.13), описывает движение и электронов, и ядер. Ее представляют в виде произведения:
Y(1, 2, 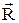 ) = YR(1, 2) Y(
) = YR(1, 2) Y( 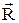 ), (18.14)
), (18.14)
где YR(1, 2) – найденная на первом этапе функция (32.9), описывающая движение электронов в поле неподвижных ядер. Подставляя (32.4) и (32.5) в (32.13), можно приближенно (с учетом m << M) получить уравнение:
{  ab(
ab( 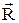 ) + E(R)} Y(
) + E(R)} Y( 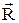 ) » E Y(
) » E Y( 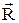 ). (32.15)
). (32.15)
Оно описывает движение ядер в поле, создаваемом электронной подсистемой. E(R) играет роль потенциальной функции, характеризующей это поле.
Так в теории адиабатического приближения удается свести задачу к двум более простым: о движении электронной и о движении ядерной подсистем. Теория адиабатического приближения используется для молекул и конденсированных сред. Во всех случаях успех достигается благодаря условию m << M.
Решение стационарного уравнения Шредингера (32.15) для сферически симметричной потенциальной ямы, изображенной на рисунке 32.2, приводит, в частности, к следующему результату. Энергия E молекулы водорода складывается из трех слагаемых:
E = EЭл + EВр + EК. (32.16)
EЭл = E(R0) – энергия, соответствующая минимуму функции E(R), изображенной на рисунке 32.2. EК – энергия колебательного движения молекулы, при котором периодически изменяются расстояния между ядрами. EВр – энергия вращательного движения молекулы как ротатора.
 Оценки порядка величин слагаемых в формуле (32.16) приводят к таким соотношениям:
Оценки порядка величин слагаемых в формуле (32.16) приводят к таким соотношениям:
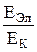 »
» 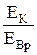 »
» 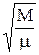 .
.
По этой причине энергетический спектр молекулы водорода (и других молекул) имеет вид, показанный на рисунке 32.5.
Малое расстояние между вращательными уровнями обуславливает полосатый спектр молекул. На рисунке 32.4 стрелками отмечены переходы, принадлежащие одной из полос излучения.
? Контрольные вопросы
1. По какому плану решается задача о молекуле водорода.
2. Запишите гамильтониан молекулы водорода. Поясните смысл каждого слагаемого.
3. На чем основано и в чем заключается адиабатическое приближение?
4. Расскажите о нахождении волновой функции электронной подсистемы молекулы водорода.
5. Расскажите об энергии электронной подсистемы молекулы водорода.
6. Почему связанные состояния атомов возникают только при антипараллельной ориентации спинов.
7. Расскажите, как решается задача о молекуле водорода на втором этапе теории адиабатического приближения.
8. Получите формулу (32.15).
9. Расскажите об энергетическом спектре молекулы водорода.
Дата добавления: 2021-11-16; просмотров: 588;











