Принцип неразличимости одинаковых частиц
& Литература: [1], [8], [3], [7].
Теория возмущения применяется как при анализе движения одной частицы, так и системы частиц – многоэлектронных атомов и молекул.
Системы одинаковых микрочастиц качественно отличаются от системы одинаковых корпускул. Отличие выражается принципом неразличимости и его следствиями. Чтобы понять смысл этого принципа, рассмотрим волновую функцию, описывающую состояние системы N одинаковых микрочастиц. Такая функция должна зависеть от полных наборов Bi, определяющих состояния всех частиц системы:
Y = Y (B1, B2, …, Bi, Bk, …, BN) Û Y(Bi, Bk). (28.1)
Введем оператор перестановок 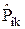 , который осуществляет преобразование волновой функции системы при обмене состояниями двух частиц (i-ой и k-ой):
, который осуществляет преобразование волновой функции системы при обмене состояниями двух частиц (i-ой и k-ой): 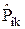 Y(Bi, Bk) = Y(Bk, Bi). (28.2)
Y(Bi, Bk) = Y(Bk, Bi). (28.2)
Найдем собственные значения оператора перестановок, то есть подберем действительные числа Pik так, чтобы выполнялось равенство:
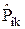 Y(Bi, Bk) = Pik Y(Bi, Bk). (28.3)
Y(Bi, Bk) = Pik Y(Bi, Bk). (28.3)
Применим оператор 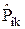 к равенству (28.3):
к равенству (28.3):
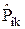 2 Y(Bi, Bk) = Pik2 Y(Bi, Bk). (28.4)
2 Y(Bi, Bk) = Pik2 Y(Bi, Bk). (28.4)
Но, исходя из смысла самого оператора 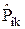 , выражаемого соотношением (28.2), можно утверждать, что двукратное применение этого оператора возвращает функции первоначальный вид:
, выражаемого соотношением (28.2), можно утверждать, что двукратное применение этого оператора возвращает функции первоначальный вид:
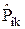 2 Y(Bi, Bk) = Y(Bi, Bk). (28.5)
2 Y(Bi, Bk) = Y(Bi, Bk). (28.5)
Сравнивая (28.5) и (28.4), приходим к выводу, что Pik2 = 1 и Þ Pik = +1 или Pik = –1. Этим двум возможным собственным значениям оператора 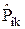 соответствуют две собственные функции Ys и Ya:
соответствуют две собственные функции Ys и Ya:
Pik = 1 Þ 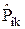 Ys(Bi, Bk) = Ys(Bk, Bi) = Ys(Bi, Bk) . (28.6)
Ys(Bi, Bk) = Ys(Bk, Bi) = Ys(Bi, Bk) . (28.6)
Pik = –1 Þ 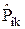 Ya(Bi, Bk) = Ya(Bk, Bi) = –Ya(Bi, Bk) . (28.7)
Ya(Bi, Bk) = Ya(Bk, Bi) = –Ya(Bi, Bk) . (28.7)
Волновая функция Ys называется симметричной, а Ya – антисимметричной.
Может ли система одинаковых микрочастиц описываться волновыми функциями, отличными от рассмотренных собственных функций оператора 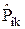 ? Постулируется, что такого быть не может. Это и утверждает принцип неразличимости: система одинаковых микрочастиц может описываться только симметричными или антисимметричными волновыми функциями. И в том, и в другом случаях квадрат модуля Y-функции не меняется при обмене частиц состояниями. Поэтому состояния системы, получающиеся посредством перестановок частиц, то есть обмена двух частиц своими состояниями, физически неразличимы. Можно сказать, что все частицы в этой системе тождественны, не имеет значения, какая именно конкретная частица оказывается в том или ином состоянии.
? Постулируется, что такого быть не может. Это и утверждает принцип неразличимости: система одинаковых микрочастиц может описываться только симметричными или антисимметричными волновыми функциями. И в том, и в другом случаях квадрат модуля Y-функции не меняется при обмене частиц состояниями. Поэтому состояния системы, получающиеся посредством перестановок частиц, то есть обмена двух частиц своими состояниями, физически неразличимы. Можно сказать, что все частицы в этой системе тождественны, не имеет значения, какая именно конкретная частица оказывается в том или ином состоянии.
Принцип неразличимости согласуется с другими положениями квантовой механики и приводит к экспериментально подтверждаемым следствиям, что доказывает его истинность.
Рисунок 28.1 иллюстрирует согласие принципа неразличимости (тождественности) с корпускулярно-волновым дуализмом. Классические частицы (корпускулы) можно различить, проследив за траекториями их движения: 1A или 2B. Для микрочастиц вместо траекторий можно указать лишь расширяющиеся в пространстве трубчатые области, в которых заметна вероятность обнаружения частиц. Если в точках A и B, принадлежащих обеим указанным трубкам, обнаружены частицы, то невозможно установить, какая из них раньше находилась вблизи точки 1, а какая – вблизи точки 2.
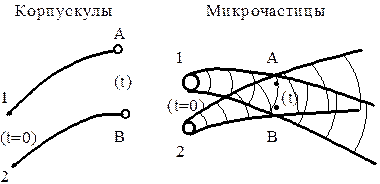 Рис. 28.1 Рис. 28.1
|
Оператор перестановок 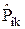 коммутирует с оператором Гамильтона
коммутирует с оператором Гамильтона  и поэтому описывает интеграл движения. Собственное значение интеграла движения должно оставаться неизменным. Следовательно, симметрия волновой функции не может измениться. Частицы, системы которых описываются антисимметричными волновыми функциями, называют фермионами, остальные – бозонами. В. Паули показал, что фермионами являются частицы с полу целыми спинами, а бозонами – с целыми.
и поэтому описывает интеграл движения. Собственное значение интеграла движения должно оставаться неизменным. Следовательно, симметрия волновой функции не может измениться. Частицы, системы которых описываются антисимметричными волновыми функциями, называют фермионами, остальные – бозонами. В. Паули показал, что фермионами являются частицы с полу целыми спинами, а бозонами – с целыми.
Из бозонов могут образовываться только бозоны. Сложная частица, состоящая из четного числа фермионов, оказывается бозоном, в то время частица, содержащая нечетное число фермионов является фермионом.
Из теоремы о разделении переменных (см. §18.) следует, что уравнению Шредингера для системы невзаимодействующих частиц удовлетворяет любая суперпозиция произведений волновых функций отдельных частиц (одно-частичных волновых функций). В качестве волновой функции системы нужно выбрать такие суперпозиции, которые бы обладали необходимой симметрией. Из этих соображений получаются выражения для волновой функции системы N частиц через одночастичные волновые функции Yi(Bk). Здесь Yi(Bk) – волновая функция k-ой частицы, находящейся в i-ом возможном состоянии. Для системы бозонов получается
Ys = 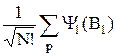 , (28.8)
, (28.8)
а для системы фермионов –
Ya = 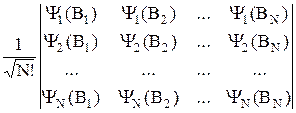 . (28.9)
. (28.9)
Коэффициент N в этих формулах обеспечивает нормировку функции на единицу. Суммирование в (28.8) проводится по всевозможным перестановкам частиц.
Из (28.9) следует запрет (принцип) Паули: в системе одинаковых фермионов в одном одночастичном состоянии не может быть более одной частицы.
Предположим, что это не так. Пусть, например, есть состояние Ya ¹ 0, при котором первая и вторая частицы находятся в одном состоянии Y1. Тогда выражение (28.9) должно содержать произведение Y1(B1) Y1(B2), что возможно лишь при равенстве двух первых строк определителя. Но такой определитель равен нулю. Это противоречит исходному утверждению Ya ¹ 0, что и доказывает принцип Паули.
? Контрольные вопросы
1. Сформулируйте принцип неразличимости одинаковых частиц и поясните смысл его названия.
2. Расскажите о связи принципа неразличимости с корпускулярно-волновым дуализмом и с туннельным эффектом.
3. Расскажите о частицах с симметричными и с антисимметричными волновыми функциями.
4. Докажите принцип Паули.
Атом гелия
& Литература: [1], [8], [3], [6].
 Рис. 29.1
Рис. 29.1
|
Анализируется модель, изображенная на рисунке 29.1. В поле неподвижного ядра с зарядом z e движутся два электрона. Для гелия z = 2. Учитываются спины электронов, которые обозначены на рисунке стрелками 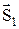 и
и 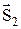 . Волновая функция системы должна зависеть от радиус-векторов
. Волновая функция системы должна зависеть от радиус-векторов  1 и
1 и  2, а также от спиновых переменных s1 и s2 каждого электрона. В нерелятивистском приближении эту функцию можно представить в виде произведения координатной и спиновой частей:
2, а также от спиновых переменных s1 и s2 каждого электрона. В нерелятивистском приближении эту функцию можно представить в виде произведения координатной и спиновой частей:
Y = Y(  1,
1,  2, s1, s2) = Y(
2, s1, s2) = Y(  1,
1,  2) Y(s1, s2) . (29.1)
2) Y(s1, s2) . (29.1)
Y-функция системы электронов должна быть антисимметричной. Поэтому симметричной спиновой части волновой функции должна соответствовать антисимметричная координатная часть и наоборот:
Y = Ya(  1,
1,  2) Ys(s1, s2) (29.2)
2) Ys(s1, s2) (29.2)
или Y = Ys(  1,
1,  2) Ya(s1, s2) . (29.3)
2) Ya(s1, s2) . (29.3)
Спиновая часть волновой функции описывает совокупность двух собственных моментов импульса 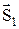 и
и 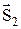 , которую можно эквивалентным образом заменить одним суммарным моментом
, которую можно эквивалентным образом заменить одним суммарным моментом 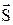 =
= 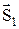 +
+ 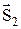 . По правилу сложения моментов импульса микрочастиц квантовое число s суммы может иметь два значения: s = 1/2 + 1/2 = 1 или s = 1/2 + 1/2 – 1 = 0. В первом случае говорят о состояниях ортогелия ↑↑(«параллельные» спины), во втором – о состояниях парагелия ↑↓(«антипараллельные» спины).
. По правилу сложения моментов импульса микрочастиц квантовое число s суммы может иметь два значения: s = 1/2 + 1/2 = 1 или s = 1/2 + 1/2 – 1 = 0. В первом случае говорят о состояниях ортогелия ↑↑(«параллельные» спины), во втором – о состояниях парагелия ↑↓(«антипараллельные» спины).
Может быть три спиновых состояния ортогелия, отличающихся значением спиновой переменной: s = 1, 0, –1, и лишь одно спиновое состояние парагелия: s = 0.
Спиновая переменная суммарного момента равна сумме спиновых переменных слагаемых: s = s1 + s2. В соответствии с этим спиновые волновые функции ортогелия Y↑↑(s) и парагелия Y↑↓(s) можно представить в виде: Y↑↑(1) = Y1(1/2) Y2(1/2) , (29.4)
Y↑↑(–1) = Y1(–1/2) Y2(–1/2) , (29.5)
Y↑↑(0) = 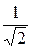 (Y1(1/2) Y2(–1/2) + Y1(–1/2) Y2(1/2)) , (29.6)
(Y1(1/2) Y2(–1/2) + Y1(–1/2) Y2(1/2)) , (29.6)
Y↑↓(0) = 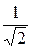 (Y1(1/2) Y2(–1/2) – Y1(–1/2) Y2(1/2)) . (29.7)
(Y1(1/2) Y2(–1/2) – Y1(–1/2) Y2(1/2)) . (29.7)
В состояниях (29.4) и (29.5) спины электронов «параллельны». Это состояния ортогелия. Обе функции симметричны. И в (29.6), и в (29.7) проекция суммарного спина на ось z равна нулю (s = 0), но (29.6) – функция симметричная, а (29.7) – антисимметричная. Чтобы переход из одного состояния ортогелия в другое не менял тип симметрии волновой функции, (29.6) следует отнести к тройке симметричных функций ортогелия, а к парагелию – единственную антисимметричную функцию (29.7).
Теперь на основании (29.2) и (29.3) можно утверждать, что ортогелию соответствуют антисимметричные координатные части волновых функций: Y↑↑(  1,
1,  2) = Ya(
2) = Ya(  1,
1,  2), (29.8)
2), (29.8)
а парагелию – симметричные:
Y↑↓(  1,
1,  2) = Ys(
2) = Ys(  1,
1,  2) . (29.9)
2) . (29.9)
Для нахождения координатной части волновой функции Y(  1,
1,  2) решается стационарное уравнение Шредингера с гамильтонианом
2) решается стационарное уравнение Шредингера с гамильтонианом
 =
= 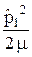 +
+ 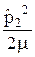 –
– 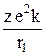 –
– 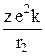 +
+ 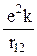 , (29.10)
, (29.10)
где k = 1 / (4 p e0).
Последнее слагаемое, характеризующее взаимодействие электронов друг с другом, можно считать оператором возмущения:
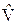 =
= 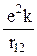 . (29.11)
. (29.11)
Тогда в нулевом приближении гамильтониан представляет собой сумму двух независимых гамильтонианов водородоподобных атомов, и можно применить теорему о разделении переменных в уравнении Шредингера. Сравнивая (29.10) с потенциальной функцией (24.1), видим, что отличие от атома водорода состоит лишь в том, что величина e2, заменяется на z e2.
На основании теоремы о разделении переменных можно сказать, что энергия атома гелия в нулевом приближении равна сумме энергий водородоподобных атомов: E » En + Em, (29.12)
где n и m – главные квантовые числа для этих атомов. Произведение соответствующих атомарных волновых функций или линейная комбинация этих произведений должны удовлетворять уравнению Шредингера. Следует подобрать такие линейные комбинации, которые обеспечивают необходимую симметрию волновой функции:
|
|
 1,
1,  2) »
2) » 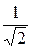 (Yn0(
(Yn0(  1) Ym0(
1) Ym0(  2) ± Ym0(
2) ± Ym0(  1) Yn0(
1) Yn0(  2)) . (29.13)
2)) . (29.13)
Знак «+» дает симметричную функцию, то есть (см. (29.9)) координатную часть волновой функции для парагелия ↑↓, а знак «–» (см. (29.8)) – для ортогелия ↑↑.
Волновые функции Y0 и энергетические уровни En водородоподобного атома предполагаются известными. В частности, из (24.10) и (24.4), заменяя e2 на z e2, получим: En = – z2 ER / n2 . (29.14)
Формулы (29.12) и (29.14) дают наименьшее значение энергии при
n = m = 1, то есть когда оба электрона находятся в основном одночастичном состоянии 1s. В этом случае отличная от нуля функция Y(  1,
1,  2) (29.13) получается только для парагелия ↑↓. Спины электронов антипараллельны, и принцип Паули не запрещает электронам находиться в одинаковых 1s-состояниях: E » E0↑↓ = E1 +E1 = – 2 z2 ER = – 8 ER. (29.15)
2) (29.13) получается только для парагелия ↑↓. Спины электронов антипараллельны, и принцип Паули не запрещает электронам находиться в одинаковых 1s-состояниях: E » E0↑↓ = E1 +E1 = – 2 z2 ER = – 8 ER. (29.15)
В случае ортогелия формула (29.13), отражающая принцип Паули, позволяет лишь одному электрону находиться в состоянии 1s. Наименьшее значение энергии для ортогелия в результате оказывается больше:
E » E0↑↑ = E1 +E2 = – 5 z2 ER / 4 = – 5 ER. (29.16)
Рисунок 29.2 иллюстрирует распределение электронов по одно-частичным состояниям – электронные конфигурации парагелия и ортогелия. Слева – основное состояние парагелия (с энергией –8 ER). Справа – основное состояние ортогелия (c энергией –5 ER). Посредине – возбужденное состояние парагелия, энергия которого тоже равна –5 ER.
Теория возмущения позволяет найти поправки к энергетическим уровням (29.15) и (29.16), обусловленные наличием оператора возмущения (29.11).
Уровень (29.15) не вырожден. Ему соответствует лишь одно состояние (29.13): Y0↑↓ = 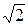 Y1s0 (
Y1s0 (  1) Y1s0(
1) Y1s0(  2) . (29.17)
2) . (29.17)
Поправка к энергии определяется по формуле (26.5):
DE↑↓ = 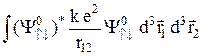 .
.
Вычисление этого интеграла дает значение DE↑↓ » 2,5 ER, что согласуется с измерениями энергии ионизации атомов парагелия.
|
|
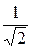 (Y1s(
(Y1s(  1) Y2s(
1) Y2s(  2) ± Y2s(
2) ± Y2s(  1) Y1s(
1) Y1s(  2)) . (29.18)
2)) . (29.18)
Нижний знак соответствует ортогелию ↑↑, а верхний – возбужденному состоянию парагелия (↑↓)′. Электронные конфигурации этих состояний –
1s1 2s1 Они показаны на рисунке 29.2.
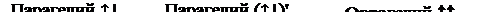 Рис. 29.2
Рис. 29.2
|
Для вычисления поправок к вырожденному уровню можно воспользоваться соотношением (26.10): 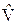 Y0 = Y0 DE .
Y0 = Y0 DE .
Получим:
DE = 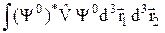 . (29.19)
. (29.19)
Для каждой из двух функций (29.18) получим свою поправку к энергии. Вырождение снимается. Интеграл (29.19) удобно представить в виде:
DE = Q ± A, (29.20)
где знак «+» – для парагелия ↑↓, знак «–» – для ортогелия ↑↑,
Q = 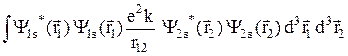 , (29.21)
, (29.21)
A = 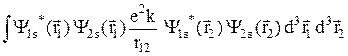 . (29.22)
. (29.22)
Величину Q называют кулоновским интегралом. На основании (29.21) можно сказать, что эта величина представляет собой энергию кулоновского взаимодействия двух электронов, находящихся в 1s и 2s состояниях, если считать, что заряды этих электронов непрерывно распределены по всему пространству.
А – обменный интеграл. Сравнение формул (29.21) и (29.22) позволяет придать величине А смысл, аналогичный кулоновскому интегралу с той лишь существенной разницей, что каждый электрон нужно считать находящимся частично в состоянии 1s, а частично – в состоянии 2s. Чтобы при этом соблюдался запрет Паули, следует считать, что электроны непрерывно обмениваются своими состояниями.
Разумеется, данную интерпретацию соотношений (29.21) и (29.22) не следует понимать буквально. Это лишь попытка привычными классическими терминами и моделями отразить специфические свойства микрочастиц.
Вся поправка (29.20) обусловлена электромагнитным взаимодействием. Но если первое слагаемое Q представляет собой среднюю энергию кулоновского взаимодействия классических заряженных частиц, то второе слагаемое А учитывает специфические квантово-механические особенности электронов, отражаемые принципом Паули. Величину А называют также обменной энергией, или энергией обменного взаимодействия. Подобная величина фигурирует при описании взаимодействия электронов и в других многоэлектронных системах, например, в молекулах или твердых телах. Именно обменное взаимодействие ответственно за так называемые ковалентные (химические) связи. Не следует забывать, что рассматриваемое здесь обменное взаимодействие электронов – лишь специфическое квантово-механическое проявление фундаментального электромагнитного взаимодействия.
Как в нулевом приближении, так и с учетом возмущения энергетический уровень основного состояния парагелия оказывается ниже уровня основного состояния ортогелия. Тем не менее, переход к основному состоянию парагелия не происходит, поскольку он запрещен правилами отбора (27.20) и (27.23). В результате гелий проявляет себя как смесь двух газов – парагелия и ортогелия, несколько различающихся своими спектрами.
? Контрольные вопросы
1. Из каких сомножителей составляется волновая функция атома гелия?
2. Расскажите об ортогелии и парагелии. Какова симметрия координатных частей их волновых функций?
3. Запишите гамильтониан атома гелия.
4. Как выглядит координатная часть волновой функции атома гелия в нулевом приближении?
5. Расскажите об энергии и электронной конфигурации основного состояния парагелия в нулевом приближении.
6. Расскажите об энергии и электронной конфигурации основного состояния ортогелия в нулевом приближении.
7. Расскажите о вычислении поправки к энергии основного состояния парагелия.
8. Расскажите о вычислении поправки к энергии основного состояния ортогелия.
Дата добавления: 2021-11-16; просмотров: 564;











