Задача о движении двух частиц.
& Литература: [1], [8].
Задача о системе двух частиц относится, например, к атому водорода, мезоатому, позитронию. Как и в классической механике, она сводится к задаче об одной частице.
 На рисунке 23.1 изображены две частицы. Их массы m1 и m2, а радиус-векторы
На рисунке 23.1 изображены две частицы. Их массы m1 и m2, а радиус-векторы 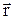 1 и
1 и 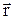 2. Величина
2. Величина 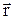 =
= 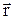 2 –
2 – 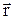 1 (23.1)
1 (23.1)
определяет положение второй частицы относительно первой. С – центр масс системы. Его радиус-вектор 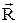 =
= 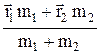 . (23.2)
. (23.2)
Гамильтониан рассматриваемой системы
 =
= 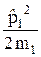 +
+ 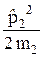 + U(r)
+ U(r)
посредством замены переменных (23.1) и (23.2) можно представить в виде суммы независимых частей:
 =
=  (
( 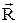 ) +
) +  (
( 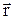 ). (23.3)
). (23.3)
Отсюда следует, что волновая функция Y( 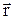 1,
1, 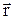 2) системы равна произведению собственных функций этих частей:
2) системы равна произведению собственных функций этих частей:
Y( 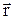 1,
1, 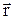 2) = Y(
2) = Y( 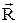 ) Y(
) Y( 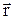 ). (23.4)
). (23.4)
Собственная функция Y( 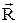 ) гамильтониана
) гамильтониана  (
( 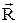 ) описывает движение частицы массой (m1 + m2), которая находится в центре масс С.
) описывает движение частицы массой (m1 + m2), которая находится в центре масс С.
Второе слагаемое в формуле (23.3) имеет вид
 (
( 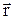 ) =
) = 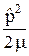 + U(
+ U( 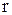 ), (23.5)
), (23.5)
где m = m1 m2 / (m1 + m2). (23.6)
Собственная функция Y( 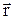 ) этого гамильтониана характеризует движение m-точки, то есть частицы массой m (10.6) и радиус-вектором
) этого гамильтониана характеризует движение m-точки, то есть частицы массой m (10.6) и радиус-вектором  (10.1), относительно центра масс С; m-точка находится в поле, потенциальная функция U(
(10.1), относительно центра масс С; m-точка находится в поле, потенциальная функция U( 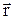 ) которого описывает взаимодействие рассматриваемых частиц.
) которого описывает взаимодействие рассматриваемых частиц.
Таким образом, задача сводится к решению стационарного уравнения Шредингера для m-точки, находящейся в центральном поле:
 (
( 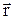 ) Y(
) Y( 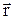 ) = E Y(
) = E Y( 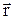 ). (23.7)
). (23.7)
Центральная симметрия обуславливает использование сферических координат r, q, j. В этих координатах гамильтониан (23.5) можно представить следующим образом:
 (
( 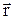 ) = –
) = – 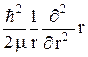 +
+ 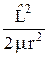 + U(r), (23.8)
+ U(r), (23.8)
где 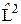 выражается формулой (22.3), то есть является оператором квадрата момента импульса.
выражается формулой (22.3), то есть является оператором квадрата момента импульса.
Благодаря (23.8) решение уравнения (23.7) можно искать в виде
Y( 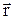 ) = R(r) Yl m (q, j), (23.9)
) = R(r) Yl m (q, j), (23.9)
где угловая часть волновой функцииYl m (q, j) является собственной функцией оператора 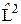 . Она определяется соотношением (22.5) и соответствует собственным значениям (22.4).
. Она определяется соотношением (22.5) и соответствует собственным значениям (22.4).
Учтя (22.4) при подстановке (23.9) и (23.8) в (23.7), получим уравнение для радиальной части R(r)волновой функции:
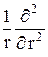 r R(r) +
r R(r) + 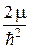 ( E – U (r) –
( E – U (r) – 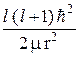 ) R(r) = 0. (23.10)
) R(r) = 0. (23.10)
Уравнение (23.10) определяет также и энергетический спектр. Видно, что энергия E не может зависеть от магнитного квантового числа m, но может зависеть от числа l.
? Контрольные вопросы
1. Как осуществляется разделение переменных при решении задачи о системе двух частиц? К каким более простым задачам она сводится?
2. Что такое m-точка? Какой она имеет смысл для атома водорода?
3. Что такое угловая и что такое радиальная части волновой функции? Какой смысл имеют содержащиеся в них квантовые числа?
4. Какую информацию об энергетическом спектре содержит в себе уравнение Шредингера для радиальной части волновой функции?
|
23.1.Получите соотношение (23.3).
23.2.Получите выражение (23.8), используя формулу для оператора Ñ2 в сферической системе координат:
Ñ2= 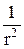
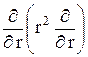 +
+ 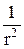
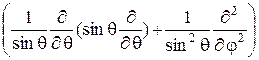 (23.11)
(23.11)
23.3. Получите уравнение (23.10).
§24. Решение квантово-механической задачи
об атоме водорода
& Литература: [1], [3], [8], [7].
Соотношения (23.9) и (23.10) справедливы для любых центрально симметричных полей. В атоме водорода поле – центрально симметричное, и оно описывается потенциальной функцией
U(r) = – k e2 / r, где k = 1 / (4 p e0). (24.1)
Целесообразно перейти к безразмерным переменным
r = r / r0 и e = – E / ER, (24.2)
где r0 = ħ2 / (m e2 k) – боровский радиус, а (24.3)
ER = k2 m e4 / (2 ħ2) – энергия Ридберга . (24.4)
Уравнение Шредингера для радиальной части R(r) волновой функции в безразмерных переменных принимает вид
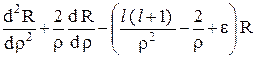 = 0. (24.5)
= 0. (24.5)
Решение уравнения (24.5) ищется в виде
R = f exp (– r 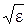 ), (24.6)
), (24.6)
так как второй сомножитель в (24.6) удовлетворяет уравнению (24.5) при r®¥. Подставляя (24.6) в (24.5), получим уравнение, которому должна удовлетворять функция f(r):
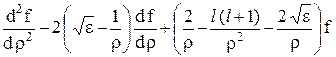 = 0. (24.7)
= 0. (24.7)
Функцию f = f(r) представляют в виде степенного ряда
f = r l 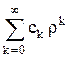 =
= 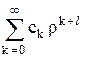 . (24.8)
. (24.8)
Нулевой член ряда (24.8) дает асимптотическое решение (24.7) при r ® 0. Коэффициенты ck должны обеспечить обращение равенства (24.7) в тождество. Тождество будет иметь место при выполнении следующего рекуррентного соотношения:
ck+1 = ck 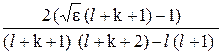 . (24.9)
. (24.9)
Сравнение степенного разложения функции r l exp (2 r 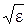 ) с рядом (24.8) приводит к заключению, что при r ® ¥ функция f ® r l exp (2 r
) с рядом (24.8) приводит к заключению, что при r ® ¥ функция f ® r l exp (2 r 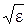 ) и, следовательно, R(r) ® ¥, чего не может быть для волновой функции. Конечность волновой функции будет обеспечена, если числитель в формуле (24.9) при k = nr обратится в нуль. Тогда ряд (24.8) станет полиномом степени l + nr, и функция (24.6) при r ® ¥ будет стремится к нулю. Этого можно достичь, подобрав параметр e так, чтобы
) и, следовательно, R(r) ® ¥, чего не может быть для волновой функции. Конечность волновой функции будет обеспечена, если числитель в формуле (24.9) при k = nr обратится в нуль. Тогда ряд (24.8) станет полиномом степени l + nr, и функция (24.6) при r ® ¥ будет стремится к нулю. Этого можно достичь, подобрав параметр e так, чтобы 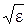 (l + nr +1) – 1 = 0, или
(l + nr +1) – 1 = 0, или
E = – ER / n2, (24.10)
где n = l + nr + 1 – (24.11)
главное квантовое число, а величину nr, определяющую степень полинома f (24.8), называют радиальным квантовым числом.
Искомая радиальная часть волновой функции (24.6) принимает вид:
R = r l Ln l (2 r / n) exp (– r 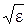 ) , (24.12)
) , (24.12)
где Ln l (x) – известные в математике полиномы Лагера аргумента x = 2 r / n. Приведем для примера несколько таких полиномов:
L10 (x) = L21 (x) = 1; L20 (x) = 2 – x; L31 (x) = 6 – x; L30 (x) = 21 –18 x + 2 x2 .
? Контрольные вопросы
1. Перечислите основные положения, используемые при решении задачи об атоме водорода.
2. Какова угловая часть волновой функции атома водорода?
3. В каком виде и почему разыскивается решение уравнения Шредингера для радиальной части волновой функции атома водорода?
4. Почему ряд, посредством которого выражается решение уравнение Шредингера, превращают в полином?
5. Расскажите о радиальном и главном квантовых числах. Какие значения может принимать число l при фиксированной величине n?
|
25.4.Приведите уравнение (23.10) к виду (24.5).
25.5.Получите уравнение (24.7).
25.6.Проверьте подстановкой, что формулы (24.6) и (24.8) при
r ® 0 удовлетворяют уравнению (24.5).
25.7.Получите рекуррентное соотношение (24.9).
25.8.Докажите, что при r ® ¥ ряд 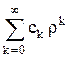 ® exp (2 r
® exp (2 r 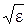 ), если коэффициенты ck удовлетворяют соотношению (24.9).
), если коэффициенты ck удовлетворяют соотношению (24.9).
§25. Энергетический спектр
и пространственная структура атома водорода.
Влияние спина электрона на энергетический спектр
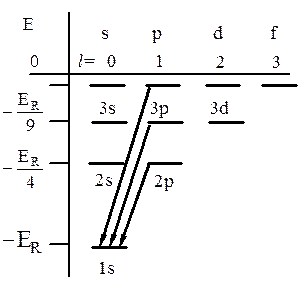 Рис. 25.1
Рис. 25.1
|
& Литература: [1], [3], [8], [7].
Энергетический спектр атома водорода определяется формулой (24.10), совпадающей с той, которая получается в боровской теории. В отличие от последней ограничение n ³ 1 не является дополнительным постулируемым условием, а непосредственно следует из (24.11). Уровни энергии атомов принято изображать схемой, показанной на рисунке 25.1. Стрелки обозначают переходы, соответствующие спектральной серии Лаймана.
Энергетические уровни атома водорода вырождены не только по магнитному, но и по орбитальному квантовому числу l. Вырождение по l называют случайным, поскольку число l содержится в исходном уравнении (23.10). Вырождение получается только в том случае, когда потенциальная функция имеет вид (24.1). В атомах щелочных металлов валентный электрон находится в поле, несколько отличающемся от кулоновского (24.1). Это приводит к снятию вырождения: уровни ns, np, nd, … на схеме, аналогичной рис.25.1, располагаются не на одной высоте.
Под пространственной структурой атома понимают распределение плотности вероятности |Y(  )|2 нахождения электрона в различных точках пространства. Точно так же распределена плотность отрицательного электрического заряда атома. Величина |Y(
)|2 нахождения электрона в различных точках пространства. Точно так же распределена плотность отрицательного электрического заряда атома. Величина |Y(  )|2 определяет вероятность dW обнаружить электрон в элементарном объеме d3
)|2 определяет вероятность dW обнаружить электрон в элементарном объеме d3  вблизи точки с радиус-вектором
вблизи точки с радиус-вектором  :
:
dW = |Y(  )|2 d3
)|2 d3  . (25.1)
. (25.1)
Чтобы представить себе пространственное распределение плотности вероятности, нужно из-за (23.9) совместить в своем воображении угловое распределение, отражаемое рассмотренными в §22 полярными диаграммами, с распределением |R(r)|2, определяемым функцией (24.12).
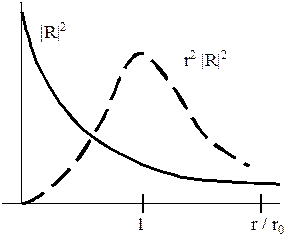 Рис. 25.2
Рис. 25.2
|
Для 1s состояния функция |R|2 изображена сплошной линией на рисунке 25.2. Видно, что плотность вероятности максимальна в центре атома и плавно убывает, существенно уменьшаясь на расстояниях порядка боровского радиуса r0. Модель боровской орбиты не согласуется с такой пространственной структурой. Для наглядного представления пространственной структуры атома более подходит модель электронного облака. Принимается, что плотность вещества, из которого состоит это воображаемое облако, пропорциональна плотности вероятности обнаружения электрона в данной точке пространства. Электронное облако 1s состояния напоминает сферически симметричный рой пчел, уменьшенный мысленно до размеров атома. Число «пчел» этого облака в единице объема плавно убывает от центра к периферии.
Иногда рассматривают вероятность dW(r) обнаружить электрон в тонком сферическом слое толщиной dr на расстоянии r от центра:
dW(r) = r2 |R|2 dr . (25.2)
Эта величина определяется радиальной плотностью вероятности r2 |R|2. График радиальной плотности вероятности для 1s состояния изображен пунктирной линией на рисунке 25.2. Он имеет максимум при r = r0. Однако это не означает, что движение электрона по боровской орбите хотя бы приблизительно отражает пространственную структуру: электрон может оказаться в любой точке вблизи ядра, а боровский электрон – лишь в точках, лежащих на орбите.
Из простых качественных соображений ясно, что учет спина электрона должен изменить формулу (24.10), описывающую энергетический спектр. Энергия взаимодействия спинового магнитного момента с орбитальным принимает различные значения для двух возможных взаимных ориентаций этих моментов. Корректный учет этого спин-орбитального взаимодействия осуществляется в релятивистской теории атома, созданной П. Дираком.
Энергетический спектр (24.10) уточняется следующим образом:
E n j = – 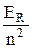 – a2
– a2 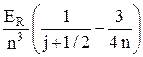 . (25.3)
. (25.3)
Второе слагаемое в этом выражении называют формулой тонкой структуры. Оно определяет тонкую структуру спектра атома водорода. Безразмерная постоянная a = k e2 / (c ħ) » 1 / 137. Это – постоянная тонкой структуры.
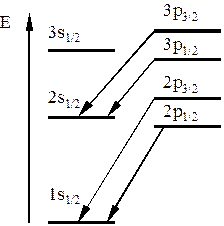 Рис. 25.3
Рис. 25.3
|
Из (12.3) видно, что энергия атома зависит не только от главного квантового числа n, но и от квантового числа j полного момента импульса 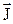 , представляющего собой сумму спинового
, представляющего собой сумму спинового 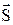 и орбитального
и орбитального 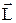 моментов:
моментов: 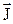 =
= 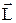 +
+ 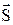 .
.
Суммирование моментов импульса микрочастиц производится по особым правилам, отражающим квантово-механические особенности микрообъектов. Правила квантования суммарного момента аналогичны правилам квантования слагаемых. Квантовое число суммарного момента может принимать несколько значений:
j = l + s, l + s – 1, … |l – s|. (25.4)
Квантовое число проекции суммарного момента равно сумме квантовых чисел слагаемых:
mj = m + s. (25.5)
Эти правила сложения моментов дает для атома водорода: j = l + ½ и
j =|l – ½|. Поэтому все энергетические уровни, кроме s-уровней (l = 0), оказываются дублетными.
Схема энергетических уровней атома водорода на самом деле несколько отличается от рисунка 25.1. Отличия отражены на рисунке 25.3 без соблюдения масштаба. Стрелкам, мало отличающимся по длине, соответствуют пары близко расположенных спектральных линий – тонкая структура. Из формулы (25.3) следует, что состояния 2s1/2 и 2p1/2 должны иметь одну и ту же энергию. На самом же деле, как было установлено У. Лэмбом и Р. Ризерфордом, уровень 2p1/2 расположен несколько ниже, чем 2s1/2, что отражено на рисунке 25.3.
Объяснение лэмбовского сдвига было с достаточной точностью дано квантовой электродинамикой. Выяснилось, что он является одним из проявлений нулевых колебаний электромагнитного вакуума.
? Контрольные вопросы
1. Нарисуйте схему энергетических уровней атома водорода.
2. Чем отличаются схемы энергетических уровней атомов щелочных металлов от рисунка 25.1?
3. Что такое электронное облако? Опишите электронные облака 1s и 2p состояний.
4. Какой физический смысл имеет радиальная плотность вероятности?
5. Что такое спин-орбитальное взаимодействие, как оно влияет на энергию атома и как теоретически учитывается?
6. Расскажите о тонкой структуре энергетического спектра атома водорода.
7. Как складываются моменты импульса микрочастиц?
8. Расскажите о лэмбовском сдвиге.
|
25.1.Подсчитайте кратность вырождения n-го энергетического уровня атома водорода, пренебрегая спином.
25.2.Сколько спектральных линий входит в состав мультиплета, соответствующего головной линии серии Бальмера? Учесть, что возможны лишь переходы, для которых Dl = ±1; Dj = ±1, 0.
25.3.Вычислите фактор Ланде gЛ, определяющий связь полного магнитного момента атома 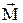 с полным моментом импульса
с полным моментом импульса 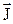 :
:
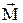 = –
= – 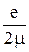 gЛ
gЛ 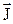 . Учтите, что гиромагнитное отношение для спинового момента импульса в два раза больше по сравнению с орбитальным.
. Учтите, что гиромагнитное отношение для спинового момента импульса в два раза больше по сравнению с орбитальным.
gЛ = 1 + 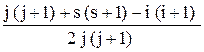 .
.
Дата добавления: 2021-11-16; просмотров: 596;











