Корпускулярно-волновой дуализм

& Литература: [1], [2], [5], [6].

Луи де Бройль (1892–1987) пытался понять, в чем же заключается особенность электронов, отражаемая постулатами Бора. В связи с эти он обратил внимание на корпускулярно-волновой дуализм света. Возникла мысль: не присущ ли такой же дуализм и электронам. Если да, то к ним тоже следует применять формулы (3.2), сопоставляя электронам некоторые волны частоты n и длины волны l, связанные соотношениями (3.2) с энергией e и импульсом p электрона. Эти волны стали называть волнами де Бройля. Идея де Бройля подкреплялась тем обстоятельством, что на длине боровских орбит укладывается целое число волн де Бройля.

Гипотеза де Бройля была подтверждена экспериментально опытами К. Девисона и Л. Джермера. Волновая природа присуща не только электронам, но и всем остальным частицам. По аналогии с оптическими микроскопами в настоящее время используются электронные микроскопы. Для исследования структуры веществ наряду с рентгенографией широко используется нейтронография, основанная на дифракции нейтронных пучков.

Доказательство волновых свойств частиц распространило проблему корпускулярно-волнового дуализма, возникшую для света, на все частицы. Как могут совмещаться в одном объекте исключающие друг друга свойства? Волна – колебания каких то величин, распространяющиеся от одной точки пространства к другой. Волна существует во всем пространстве. В электромагнитной волне колеблются векторы напряженности и индукции электромагнитного поля. В звуковой волне колеблется давление в каждой точке. А что колеблется в волне де Бройля? И как согласовать волновую природу электрона с его локализацией в отдельных точках?

Для ответа на последний вопрос заманчивой казалась идея считать электрон не монохроматической волной де Бройля, а пакетом таких волн с близкими волновыми числами. Размер области локализации пакета Dx связан с интервалом волновых чисел Dk соотношением:

Dx Dk > 2 p. (4.1)

Групповая скорость пакета волн де Бройля оказывается равной скорости движения электрона. Однако идея считать электрон пакетом волн оказалась несостоятельной, поскольку пакет волн де Бройля расплывается за время порядка 10^–26 с, электрон же стабилен.

Тем не менее, описание электрона посредством пакета волн де Бройля выявляет важное свойство электронов – соотношение неопределенностей. Используя (3.2), получим из (4.1) соотношение между неопределенностями импульса Dp и координаты Dx: Dx Dp > h. Более точно соотношение неопределенностей было установлено в 1927 году В. Гейзенбергом (1901–1976):

Dx Dp_x ≥ ħ / 2. (4.2)

Это соотношение дает ключ к решению проблемы корпускулярно-волнового дуализма. Пространственная локализация волнового пакета достигается неопределенностью длин волн (волновых чисел k), характеризующих этот пакет (4.1). Неопределенность координаты электрона Dx тем меньше, чем больше неопределенность соответствующей проекции импульса Dp_x (4.2). Проблема корпускулярно-волнового дуализма оказывается связанной с проблемой неопределенностей координат и импульсов частиц.

Соотношение неопределенностей Гейзенберга (4.2), казалось бы, противоречит неуклонному прогрессу измерительной техники. В связи с этим были предложены мысленные эксперименты по возможно более точному определению координаты и импульса электрона. Анализ этих экспериментов показывает, что увеличение точности измерения координаты всегда сопровождается уменьшением точности измерения импульса, и наоборот. Погрешности измерений удовлетворяют соотношением (4.2). Причиной такого положения является неконтролируемое воздействие, которое неизбежно оказывают макроскопические приборы на микрообъекты.

Противоречия и парадоксы, связанные с соотношением неопределенности Гейзенберга и отображаемым им корпускулярно-волновым дуализмом, снимаются, если признать, что состояние микрочастицы, в отличие от классической частицы (корпускулы), не задается указанием координаты и импульса. Эти величины можно применять для описания микрочастиц лишь приблизительно, в рамках соотношения (4.2). Совсем отказаться от использования координат и импульсов тоже нельзя, поскольку все измерения проводятся макроскопическими приборами, которые оперируют указанными классическими величинами. Существуют два взаимно исключающих класса приборов. Вооружившись приборами одного из них, можно точно измерить координату частицы безо всякой информации о каких-то волнах, что аналогично исследованию корпускулы. Вооружившись приборами другого класса, можно точно измерить импульс частицы, или длину волны безо всякой информации о координате частицы, что аналогично исследованию волн. Таким образом, микрочастица – и не корпускула, и не волна. Но в одних условиях ее поведение аналогично волнам, а в других – корпускулам.

Как же описывать состояние «не корпускулы и не волны»? И какой смысл имеют обнаруженные экспериментально волны де Бройля? Правильные ответы на эти вопросы нашел М. Борн (1888–1930). Состояние частицы описывается волной де Бройля, пакетом волн или иной комплексной функцией Y( 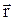, t) радиус-вектора 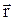и времени t. Квадрат модуля этой волновой функции (Y-функции) характеризует вероятность нахождения частицы вблизи точки 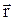. Так что область локализации пакета волн де Бройля это не область, в которой наиболее интенсивно что то колеблется, а область, в которой вероятность обнаружить электрон больше, чем вне этой области. Вероятностный смысл Y-функции порождает сомнение, описывает ли эта функция отдельную микрочастицу или большое число таких частиц – статистический ансамбль. Сомнение рассеяли опыты Л. Бибермана, Н. Сушкина и В. Фабриканта по наблюдению дифракции электронов, летящих практически поодиночке. Так что вероятностное поведение, а, следовательно, и волновые свойства, относятся к отдельным микрочастицам. Статистический ансамбль лишь позволяет выявить и измерить вероятностное их поведение.

Рассмотренные здесь проблемы, с которыми столкнулась физики при исследовании микрочастиц и возникшие при их разрешении новые идеи, явились истоками создания строгой теории – квантовой механики, с основными положениями которой далее предстоит познакомиться.

? Контрольные вопросы

1. В чем суть гипотезы де Бройля, и каковы предпосылки ее появления?

2. Записать выражение волны де Бролья в комплексной форме.

3. Чему равна длина волны де Бройля?

4. Какие наблюдения доказывают волновую природу электронов?

5. В чем суть проблемы корпускулярно-волнового дуализма?

6. Какие свойства волновых пакетов сделали привлекательной попытку решить проблему корпускулярно-волнового дуализма, отождествив электрон с пакетом волн де Бройля?

7. Почему нельзя электрон отождествить с волновым процессом, локализованным вблизи некоторой точки?

8. Расскажите о связи соотношения неопределенностей Гейзенберга со свойствами волнового пакета.

9. Почему невозможно точно измерить координату и импульс микрочастицы?

10. Как разрешается противоречие корпускулярно-волнового дуализма?

11. Расскажите о статистическом смысле волн де Бройля.

F

Задания

Д.4.1. Опыты Девисона и Джермера.

Наблюдения, свидетельствующие о волновой природе пучка электронов: интерференционные максимумы, зеркальное отражение от поверхности кристалла, интерференционное отражение. Количественная проверка гипотезы де Бройля.

Д.4.2. Пакеты волн.

Что такое пакет волн. Локализация волновых пакетов. Фазовая и групповая скорости пакета. Расплывание пакета волн де Бройля.

Д.4.3. Мысленные эксперименты по измерению координат и импульсов частиц.

Измерение координаты электрона посредством щели. Измерение положения частицы с помощью микроскопа.

4.1. Электрон, движущийся со скоростью v = 6×10⁶ м/c, попадает в однородное ускоряющее электрическое поле напряженностью E = 5×10² В/м. Какое расстояние x должен пролететь электрон в таком поле, чтобы длина волны его стала равной l = 0,1 нм?

x = 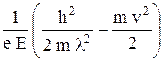= 9,6×10^–2 м.

4.2. Выразить фазовую скорость v_ф волн де Бройля, через скорость v движения электрона. v_ф = c² / v.

4.3. Выразить групповую скорость v_г пакета волн де Бройля, через скорость v движения электрона. v_г = v.

4.4. Электрон с энергией E = 1 кэВ оставляет в камере Вильсона след толщиной Dx = 1 мкм. Какова относительная неопределенность его импульса Dp_x / p_x? Можно ли по этому следу заметить отклонение в движении электрона от законов классической физики?

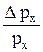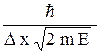= = 6×10^–6.