Расчет сварных соединений
2.3.5.1 Стыковые соединения
Для большинства сварных соединений преобладающим является нагрузка с малым общим числом циклов, поэтому основным расчетом является расчет по номинальным напряжениям.
Стыковые швы на прочность рассчитываются по номинальному сечению без учета усиления шва. Тавровые и угловые швы с глубокой проплавкой также можно рассматривать в качестве стыкового шва.
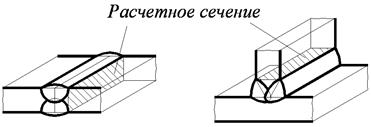
В качестве расчетного сечения берется сечение по границе наплавленного и основного металла (см. рис. 2.32), так как это оно меньше по площади поперечного сечения, чем площадь шва, и в то же время, оно ослаблено термическим влиянием сварки.
|
| Рис. 2.32. Расчетное сечение стыкового шва |
Типовые схемы для расчета стыковых швов с нагрузками, действующими в плоскости соединения, показаны в табл. 2.2.
Таблица 2.2
Схемы для расчета стыковых швов
| Растяжение (сжатие) | |
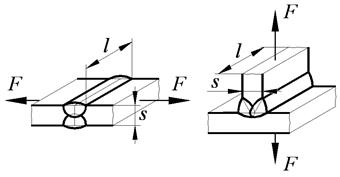
| 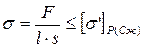 l – длина шва;
s – толщина соединяемых деталей.
Допускаемая сила (растягивающая или сжимающая):
l – длина шва;
s – толщина соединяемых деталей.
Допускаемая сила (растягивающая или сжимающая):
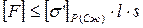 . .
|
| Поперечный изгиб | |
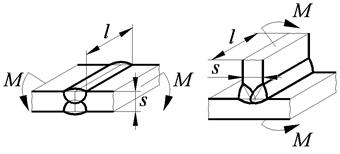
| 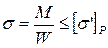 ,
где W – момент сопротивления расчетного сечения; для случая поперечного изгиба: ,
где W – момент сопротивления расчетного сечения; для случая поперечного изгиба:
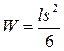 . .
|
| Продольный изгиб | |
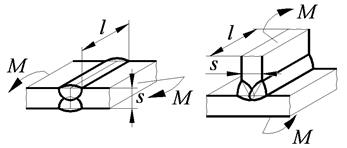
| 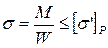 ,
где W – момент сопротивления расчетного сечения; для случая продольного изгиба: ,
где W – момент сопротивления расчетного сечения; для случая продольного изгиба:
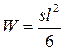 . .
|
Напряжение от одновременного действия изгибающего момента и растяжения (сжатия):
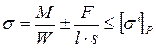
Угловые соединения
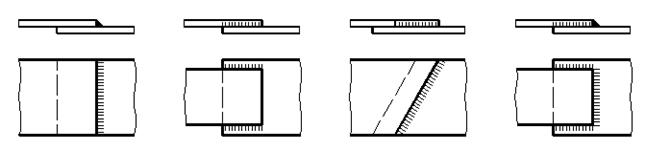
Угловыми швами выполняются нахлесточные и часть угловых и тавровых соединений. В зависимости от направления шва к направлению действующих сил соединения бывают лобовыми (рис. 2.33а), фланговыми (рис. 2.33б), косыми (рис. 2.33в), комбинированными (рис. 2.33г).
| |||
| а | б | в | г |
| Рис. 2.33. Виды угловых швов |
Максимальная длина лобового шва не ограничивается. Длину фланговых швов следует принимать не более 50k, где k – длина катета шва. Принимается kmin = 3 мм, если толщина металла s ³ 3 мм. Перекрытие нахлесточных элементов должно быть не менее 4s.
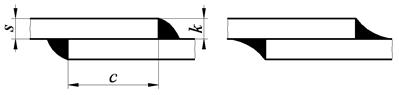
Форма поперечного сечения углового шва бывает нормальной (в виде равнобедренного треугольника) (рис. 2.34а) или улучшенной (в виде вогнутого треугольника с основанием большим, чем высота) (рис. 2.34б), обеспечивающая плавное сопряжение наплавленного металла с основным.
| 
| |
| а | б | Рис. 2.35 Форма поперечного сечения углового шва |
| Рис. 2.34. Форма сечения угловых швов | ||
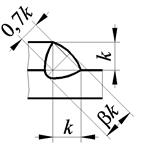
Расчет прочности угловых швов всех типов производится на срез по критическому, т.е. наименьшему сечению, проходящему через биссектрису прямого угла (рис. 2.35). Чем глубже проплавление, тем больше площадь сечения. Для разных видов сварки принимается разный коэффициент проплавления b:
b = 0,7 – при ручной сварке с любым количеством проходов;
b = 0,7 – при многопроходной автоматической, полуавтоматической сварке;
b = 0,8 – при 2- и 3-проходной полуавтоматической сварке;
b = 0,9 – при 2- и 3-проходной автоматической сварке;
b = 1,1 – при однопроходной автоматической сварке;
Площадь расчетного (критического) сечения:
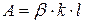
Расчет угловых швов при нагружении силой в любом направлении:
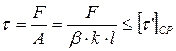 ,
,
или 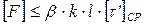 .
.
При действии поперечной силы в плоскости соединения расчетные схемы показаны в табл. 2.3.
Таблица 2.3
Схемы для расчета угловых швов
при действии поперечной силы в плоскости стыка
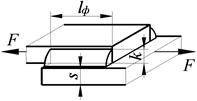
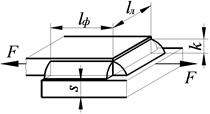
| Лобовой шов | Фланговый шов | Комбинированный шов |
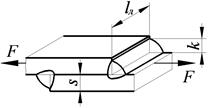
| 
| 
|
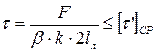
| 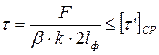
| 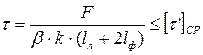
|
При нагружении моментом в плоскости соединения расчетные схемы показаны в табл. 2.4.
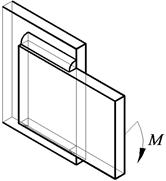
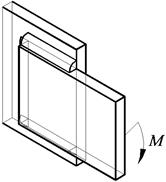
При нагружении моментом в плоскости, перпендикулярной плоскости соединения, расчетная схема показана на примере нагружения комбинированного шва (табл. 2.5).
Таблица 2.4
Схемы для расчета угловых швов при действии момента в плоскости стыка
| Лобовой шов | Фланговый шов | Комбинированный шов | |
| Рисунок | 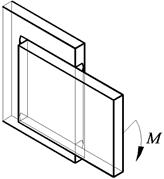
| 
| 
|
| Расчетная схема | 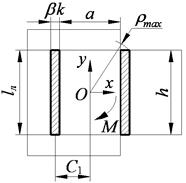
| 
| 
|
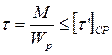 ; ;
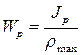 ; ;
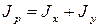 ; ;
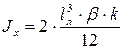 ; ;
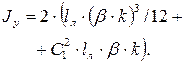
| 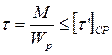 ; ;
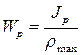 ; ;
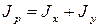 ; ;
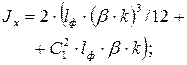
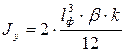 . .
| 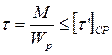 ; ;
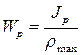 ; ;
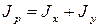 ; ;
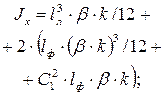
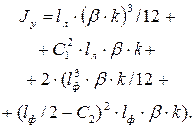
| |
(∙)О – центр тяжести сечения всех сварных швов;
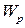 – полярный момент сопротивления расчетного сечения; – полярный момент сопротивления расчетного сечения;
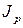 – полярный момент инерции расчетного сечения; – полярный момент инерции расчетного сечения;
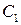 , , 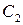 – расстояние от центра тяжести сечения всех сварных швов до центра тяжести отдельных швов. – расстояние от центра тяжести сечения всех сварных швов до центра тяжести отдельных швов.
|
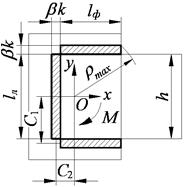
Таблица 2.5
Схема для расчета угловых швов при действии момента в плоскости, перпендикулярной плоскости соединения
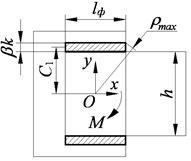
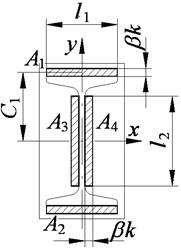
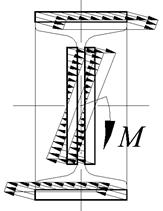
| Схема соединения | Схема для расчета момента сопротивления сечения сварного шва | Распределение напряжений в сечении сварного шва |
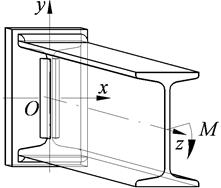
| 
| 
|
Комбинированный шов разбит на 4 простых шва: А1–А4.
Максимальное напряжение в сечении швов, вызываемое изгибающим моментом:
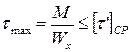 .
Момент сопротивления сечения шва относительно оси x: .
Момент сопротивления сечения шва относительно оси x:
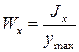 ,
где ,
где 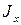 – момент инерции сечения шва; – момент инерции сечения шва;
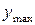 – расстояние от оси x до максимально удаленной точки сечения шва: – расстояние от оси x до максимально удаленной точки сечения шва:
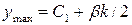 .
Момент инерции составного сечения шва: .
Момент инерции составного сечения шва:
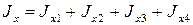 Моменты инерции сечений простых швов:
Моменты инерции сечений простых швов:
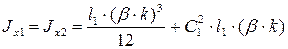 ; ; 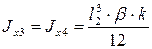 ,
где ,
где 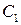 – расстояние от оси x до центра тяжести швов А1 и А2. – расстояние от оси x до центра тяжести швов А1 и А2.
|
Дата добавления: 2018-05-10; просмотров: 1490;











