ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ХАРАКТЕРИСТИК НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

Важную роль в расчетах цепей с нелинейными элементами имеют характеристики нелинейного элемента. Основное внимание уделяется вольт-амперным характеристикам (ВАХ), поскольку они отражают зависимость тока, протекающего в данный момент времени, от напряжения. Аналитическое выражение статических ВАХ нелинейного элемента (НЭ) в точном виде практически невозможно, так как зачастую она состоит из нескольких криволинейных участков, описываемых различными функциями. Во многих расчетах применяют графическое определение параметров. Статические ВАХ нелинейных элементов бывают двух типов: однозначные и многозначные. В первом случае одному значению напряжения соответствует одно значение тока, а во втором случае одному значению напряжения соответствует несколько значений тока и наоборот, одному значению тока соответствует несколько значений напряжения. Графическое представление ВАХ делает процесс расчета параметров наглядным. Следует отметить, что, в отличие от линейных элементов, цепи с НЭ не поддаются точному расчету, а только приближенному. Вычерчивание ВАХ во многих методах является первостепенной задачей, поскольку от точности выполнения графика зависит точность нахождения параметров. При изучении графического представления ВАХ следует уделить внимание следующим вопросам.

1. Какие участки характеристик можно считать линейными, а ка

кие нелинейны?

2. Как выбирается точка покоя и рабочий участок?

3. Какие изменения в работу цепи вносит нелинейность ВАХ?

1.1 . Вольт-амперные характеристики диодов

Полупроводниковые диоды нашли широкое применение в нелинейных цепях. На их основе построены такие электронные приборы, как усилители мощности электрических сигналов, преобразователи частоты, генераторы гармонических колебаний, стабилизаторы и многие другие, работа которых возможна только благодаря нелинейным свойствам диодов. Однако, тип статических нелинейных вольт-амперных характеристик существенно различен для разных типов диодов. Так, например, силовые диоды имеют однозначную ВАХ, а стабилитроны и специальные диоды – многозначные ВАХ различных видов. В частности, статическая ВАХ наиболее широко используемых туннельных диодов многозначная. В связи с подобным существенным различием статических характеристик режимы работы и расчет рабочих параметров диодов различен.

а) Характеристики и параметры силового диода.

Статическая ВАХ силового диода является однозначной. Она во многом аналогична входным характеристикам ламп и биполярных транзисторов. Поэтому на ее примере можно показать основные принципы простейшего графо-аналитического способа определения параметров.

Все параметры нелинейного элемента разделяются на статические, динамические и средние. Все они могут быть вычислены по статическим ВАХ и применяются в зависимости от поставленной задачи.

На рис.1.1. представлена статическая ВАХ силового диода.

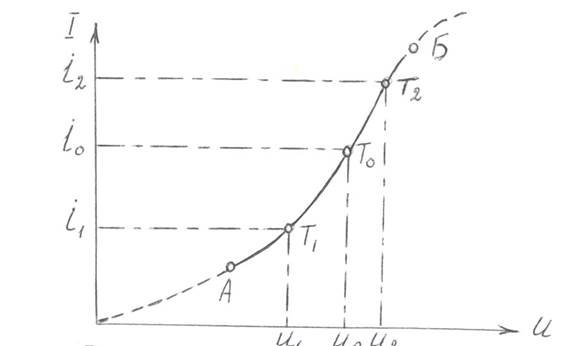
Рис. 1.1. Вольт-амперная характеристика силового диода

Из рисунка видно, что это кривая линия, так как диод – нелинейный элемент. Теоретически ВАХ выражается формулой:

i = a_d(e^buq/kT – 1), (1. 1)

где:

i - ток;

u - напряжение;

q - заряд носителя электрического заряда (электрона или дырки);

a_d - коэффициент диффузионного тока;

b - постоянная диффузионного тока;

k - постоянная Больцмана;

Т - абсолютная температура (в градусах Кельвина).

Практически эта формула хорошо выполняется только в средней части ВАХ. Вблизи нулевого напряжения и при очень больших напряжениях (режим насыщения) наблюдаются существенные отступления от формулы (1.1). На рис. 1.1. эти участки показаны пунктиром.

В статическом режиме по диоду протекает постоянный ток. Напряжение и сила тока не изменяются во времени. Этому режиму соответствует некоторая точка на ВАХ (u₀,i₀). В этом случае можно вычислить статическое внутреннее сопротивление диода и, соответственно, статическую крутизну (см. ч.1 стр.26-27).

В динамическом режиме через диод протекает переменный ток, величина напряжения и тока изменяются во времени. От перепадов напряжения будет зависеть способ вычисления крутизны. Крутизна в данном случае является динамическим параметром и ее величина не будет одинаковой для всех точек характеристики. Для полного расчета динамического режима всю ВАХ условно разбивают на участки: от 0 до точки А – нелинейная часть; от точки А до точки Б – прямолинейная (линейная) часть; выше точки Б – нелинейная часть. От А до Б - длина отрезка, который считают (аппроксимируют) прямой линией. Она в большой степени зависит от требуемой точности расчетов.

Если наименьшая и наибольшая величина тока в динамическом режиме соответствуют линейному участку, то вычисленная крутизна не отличается от статической, поскольку она равна тангенсу угла наклона прямой к оси абсцисс.

Если же хотя бы один из уровней напряжения (тока) выходит за пределы участка А-Б, то необходимо вычислять собственно динамическую крутизну.

Часто в электрических цепях через НЭ протекают две составляющие тока: постоянная и переменная, причем переменный ток представляет собой гармоническое колебание (так называемый моногармонический режим или одночастотное устройство). В этом случае статическая крутизна, соответствующая постоянной составляющей тока относится к точке Т₀, называемой точкой покоя.

S₀ = 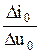- статическая крутизна,

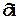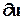где дифференциалы тока и напряжения: и заменены приращениями ( 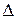), взятыми относительно точки покоя;

i₀ и u₀ – ток и напряжение постоянной составляющей.

Точка ВАХ, соответствующая разности постоянного тока и амплитуды переменного тока - нижняя точка рабочего участка (Т₁).

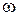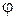u₁ = u₀ - U_maxcos( t + _u) ,

i₁= i₀ - I_maxcos( 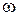t + _i).

Точка, соответствующая сумме постоянной составляющей и амплитуды переменной составляющей тока – верхняя точка рабочего участка (Т₂).

u₂ = u₀ + U_maxcos( t + _u),

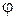i₂= i₀ + I_maxcos( t + _i).

Таким образом, рабочий участок расположен на статической ВАХ от точки Т₁ до точки Т₂. В приборах класса А точку покоя Т₀ выбирают в середине рабочего участка.

Для тех режимов, рабочий участок которых находится в пределах линейной части ВАХ, крутизна неизменна и равна статической крутизне. Во всех других случаях следует учитывать изменение крутизны. Т.е. применять динамическую крутизну.

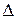
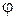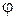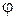Строго говоря, на практике, между током и напряжением в нелинейных цепях существует разность фаз, так как сопротивление цепи величина комплексная: = _u - _i

Это значит, что максимум тока достигается не в тот же момент, что и максимум напряжения, из-за чего точное вычисление динамических параметров, прежде всего крутизны, весьма затруднено.

В практических расчетах часто используются средние параметры, так как более точно отражают протекающие процессы. Рассмотрим понятие средней крутизны.

Переменная составляющая напряжения в гармоническом и символическом (комплексном) виде:

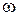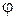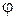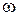U_maxcos( t + _u) = U_max е^{j u} е^{j t},

где:

U_max – мгновенная амплитуда напряжения;

U_max е^{j 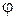u} – комплексная амплитуда напряжения.

Аналогично, переменная составляющая тока в гармоническом и символическом виде:

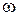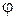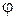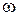I_maxcos( t + _i) = I_max е^{j i} е^{j t},

где:

I_max – мгновенная амплитуда тока;

I_max е^{j 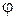i} – комплексная амплитуда тока.

Динамическая крутизна, по определению, равна отношению:

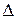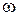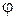S_i = [U_maxcos( t + _u)]/ 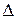I_maxcos( 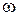t + _i).

Средняя крутизна, согласно определению, вычисляется для отдельной гармоники как отношение средней комплексной амплитуды тока данной гармоники к комплексной амплитуде напряжения.

Ввиду того, что наибольший вклад во многих устройствах вносит первая гармоника, Ю.Б.Кобзарев предложил средней крутизной считать отношение средней комплексной амплитуды тока основной (первой) гармоники к комплексной амплитуде ее напряжения:

S_ср = I_max.ср е^{j u} /U_max е^{j i} (1.2)

В расчетах именно эта величина и будет определяться графически по статическим ВАХ. Если реактивные составляющие НЭ таковы, что разность фаз 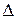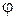близка к числу кратному 180 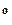(т.е. n 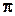, где n – целое число), то средняя крутизна практически равна отношению мгновенных амплитуд. Во многих случаях именно мгновенные амплитуды тока и напряжения поддаются измерению. Соответственно, в этих случаях точность вычислений будет тем больше, чем меньше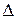 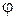отличается от n .

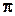Сравнивая понятия параметров, можно сделать вывод, что при уменьшении амплитуды переменной составляющей средняя крутизна стремится к дифференциальной.

Существуют следующие правила использования параметров: если рабочий участок несколько больше линейной части статической ВАХ (u<0,2u₀), то применяют динамические параметры; если же амплитуда переменного напряжения велика (одного порядка с u₀), то применяют средние параметры.

Динамическая крутизна отличаются по величине от статической и от средней в нелинейном режиме работы. Существует несколько способов учета этого различия. Наиболее типичным является разложение в ряд Тейлора динамической крутизны относительно статической крутизны:

S_i = S₀ + S^/ (u–u₀) + 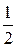S^//(u–u₀)² + 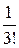S^///(u–u₀)³ + . . . +

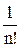+ S⁽ⁿ⁾ (u–u₀)ⁿ (1.3)

где S^/, S^//, . . ., S⁽ⁿ⁾ – производные крутизны по напряжению, соответственно, первого, второго и более высоких порядков;

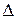u = (u – u₀) – приращение напряжения в точке покоя.

С учетом разложения (1.3) получим выражение, связывающее ток с напряжением:

i = (S₀ + 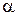₁S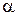^/ + ₂ S^// + . . . + _nS⁽ⁿ⁾) u (1.4)

В простейшем случае достаточно ограничиться первой производной, в более точных расчетах учитываются и высшие производные.

i = (S₀ + 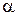₁S^/ ) u. (1.5)

б) Характеристики и параметры туннельного диода.

ВАХ многих специальных диодов относятся к многозначной.

Такие характеристики бывают двух типов: N-образные и S-образные, что показано на рис. 1.2.

Рис.1.2 . Многозначные ВАХ: а) N-образная; б) S-образная.

N-образной характеристике одному напряжению соответствует несколько токов. В S –образной характеристике нескольким напряжениям соответствует один ток.

ВАХ туннельного диода N-образная. Она имеет перегиб, которому соответствует отрицательное внутреннее сопротивление. Именно этот участок ВАХ и используется в работе, потому что в таком режиме туннельный диод обладает усилительными свойствами. На рис.1.3. представлена ВАХ туннельного диода, на которой показаны точки линейного рабочего участка.

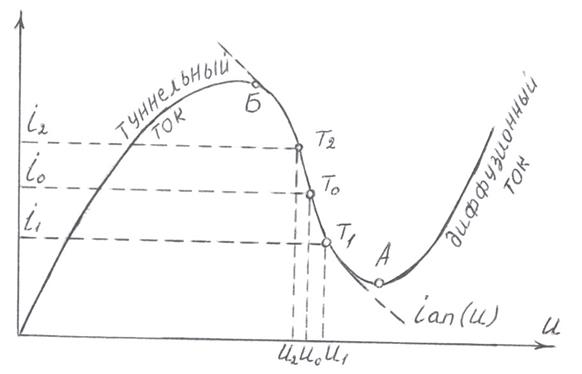
Рис. 1.3. Вольт-амперная характеристика туннельного диода

Статическая ВАХ туннельного диода теоретически выражается суммой двух экспонент:

i = a_tue^-Вu + a_d(e^bqu/kT – 1) (1.6)

где:

u - напряжение;

a_t - коэффициент туннельной составляющей тока;

В - константа, характеризующая туннельные свойства данного диода;

a_d - коэффициент диффузионной составляющей;

b - константа, характеризующая данный диод;

q - заряд носителя;

k - постоянная Больцмана;

Т - абсолютная температура (в градусах Кельвина).

Первая экспонента в (1.6) описывает ВАХ при малых напряжениях (до перегиба), а вторая – при больших напряжениях (после перегиба). Однако, на практике есть отклонения от этой формулы в области очень малых и максимальных токов.

Для расчета параметров используются различные аппроксимирующие функции, так как эта статическая ВАХ полностью нелинейна. Подбором экспонент можно добиться совпадения до 6%, но этот метод очень трудоемкий и редко применим на практике. Если амплитуда напряжения динамического режима мала (u<0,1u₀), где u₀-напряжение статического режима (постоянной составляющей), то рабочий участок (Т₁–Т₂ ) считают линейным.

ВЫВОДЫ:

1. Статические вольт-амперные характеристики полупроводнико-

вых диодов нелинейны и не могут быть точно выражены аналитически.

2. Для характеристики режимов работы НЭ используют статичес-

кие, динамические и средние параметры. Основным параметром явля-

ется крутизна.

3. В зависимости от амплитуды переменного напряжения выбира- ется тип параметров, применяемых в расчете: для малых амплитуд – статическая и динамическая крутизна; для больших амплитуд - средняя крутизна.

1.2. Характеристики электровакуумных ламп.