ГЛАВА 2. АППРОКСИМАЦИЯ ХАРАКТЕРИСТИК
НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Прежде, чем проводить расчет сложных электрических цепей необходимо определить параметры самого НЭ. В предыдущей главе были описаны общие свойства статических ВАХ и простейший метод определения величин основных параметров с использованием графически представленных вольт-амперных характеристик. Часто требуется получить решение задачи в общем виде, не связанном с конкретными численными значениями параметров, то есть, в виде формул, отражающих зависимость тока, протекающего через НЭ, от напряжения, воздействующего на него. В таком случае используется аналитический метод на основе определения математической формулы, описывающей характеристику с достаточной степенью точности. Такие методы называются аппроксимацией. Широкое применение на практике нашли методы подбора подходящих приближенных (аппроксимирующих) функций: степенного многочлена, экспоненты, отрезков прямых линий и др.
Аппроксимирующие функции позволяют аналитически определять параметры НЭ. Всю ВАХ условно разбивают на участки, соответственно режиму работы. Каждый участок может быть использован не только для графического, но и для аналитического определения параметров. При изучении этих методов следует уделить внимание следующим вопросам:
1. Как выбрать аппроксимирующую функцию при аналитичес-
ком расчете?
2. Как определить положение рабочих точек и выполнить пост-
роение для вычисления коэффициентов графо-аналитическом расчете?
3. Какой метод расчета выбрать для динамического режима
большого сигнала?
2.1. Общие сведения о выборе метода расчета и аппроксимации
В общем случае к нелинейному элементу, работающему в аппара-
туре, приложено напряжение (воздействие), имеющее две составляющие: постоянную и переменную. Это напряжение и определяет рабочую область НЭ.
Расчет любого режима работы НЭ начинают с нахождения на статических ВАХ точек рабочего участка, соответствующего той части характеристики, которая охвачена приложенным воздействием. Для расчета не обязательно строить точки графически, но можно знать их координаты.
При рассмотрении линейных элементов отмечалась независи-
мость их собственных параметров от внешнего воздействия: напряжения, тока температуры и др. Особенностью всех НЭ является зависимость параметров от величины приложенного напряжения и протекающих токов. Эта зависимость, в большинстве динамических режимов, как правило, не выражается прямой линией.
Например: Пусть НЭ имеет квадратичную зависимость между током и напряжением:
i = a2u 2, u >0 (2.1)
где a2 – постоянный коэффициент.
Тогда проводимость цепи равна: G = 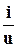 = a2u,
= a2u,
а крутизна ее характеристики S= 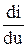 =2 a2u.
=2 a2u.
Оба эти параметра зависят от напряжения, а к цепи в целом не применим принцип суперпозиции (см.Часть1, стр.24-25).
На рис.2.1 приведена входная ВАХ биполярного транзистора, на которой показаны изменения формы сигналов при нелинейном динамическом режиме работы. Воздействие u(t)=U0+Umaxcos 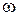 t.
t.
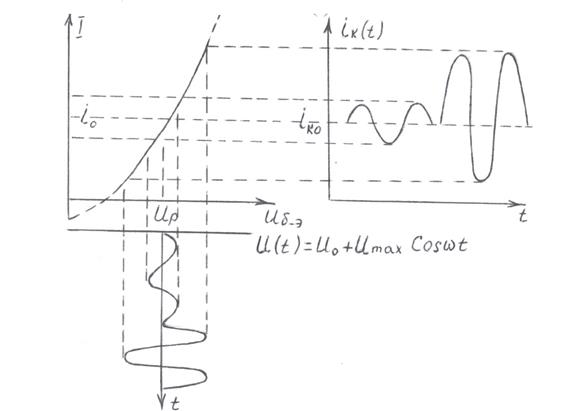
Рис.2.1. Режимы работы биполярного транзистора
Как видно из рисунка, большой сигнал подвергся сильным нелинейным изменениям. Изменение формы малого сигнала невелико, так как мала амплитуда входного переменного напряжения.
Как известно, любой сложный сигнал можно представить в виде ряда Фурье, первый член которого и есть основная гармоника. Она выражает гармоническое воздействие на НЭ. В динамическом режиме в выходной сигнал добавились более высокие частоты – высшие гармоники. На практике обычно отсеивают высшие гармоники с помощью фильтров.
Строго говоря, в выходном сигнале всегда добавляются высшие гармоники из-за нелинейности ВАХ, и их вклад будет тем больше, чем больше приложенное воздействие. В практических расчетах различают динамические режимы по величине приложенного к НЭ напряжения.
а) Динамический режим малого сигнала.
Малыми считаются сигналы, при которых выходной сигнал одного порядка с величиной статического входного сигнала (u0).
В этом случае можно использовать статические параметры.
б) Динамический режим большого сигнала дает сильные нелинейные искажения, требующие учета высших гармоник.
В этом режиме используется средняя крутизна Sср, согласно вы- ражению (1.2).
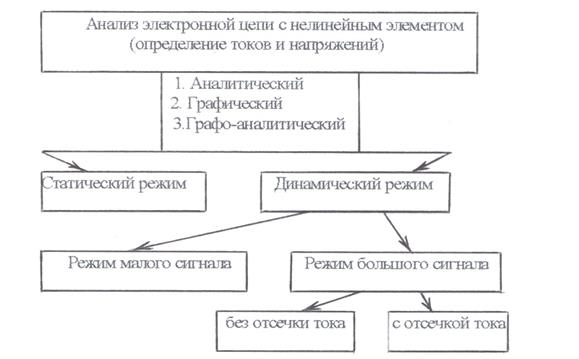
Методы расчета параметров НЭ, представлены на рис.2.2.
_
Рис.2.2 Классификация методов расчета
При графическом методе анализа характеристика НЗ и воздействие задаются в виде графиков. Форма выходного сигнала определяется путем построения третьей проекции по двум данным (рис.2.3).
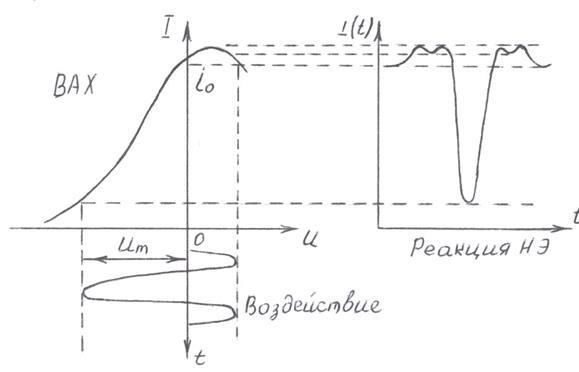
Рис.2.3. Графическое определение реакции НЭ
Недостаток этого метода в том, что невозможно получить точной количественной оценки
При аналитическом методе воздействие и характеристика заданы в виде формул. Определение реакции НЭ делается математическими методами. Метод дает точный количественный результат и применяется в настоящее время для машинного расчета.
При графо-аналитическом методе характеристика НЭ задается графически, а воздействие аналитически. Так как воздействие является функцией времени, то для каждого момента времени параметры рассчитываются с помощью графика.
ВЫВОДЫ:
1. В зависимости от амплитуды переменного воздействующего на-
напряжения в динаминамическом режиме выходной сигнал обогаща- ется высшими гармониками.
2. Существует несколько типов динамического режима работы НЭ,
и, сответственно этому, несколько методов расчета параметров.
3. Динамический режим малого воздействующего сигнала имеет
параметры статического режима. Расчет динамического режима боль-шого сигнала на практике производится аналитически или графо-анали- тически.
2.2. Аппроксимация характеристик многочленом
Для определения реакции НЭ, выражаемой силой тока, на воздействие, выражаемое входным напряжением, часто выбирают аппроксимирующую функцию в виде многочлена. Т.е. статическую ВАХ заменяют степенным многочленом с необходимой степенью точности.
i(t) = f (u), (2.2)
где:
i(t) - ток (реакция);
u(t) - напряжение (воздействие);
f (u) = f (u,t) - функция, в общем случае, нелинейная.
На практике для аналитического описания этой зависимости стремятся реальную характеристику НЭ заменить приближенной более простой. В этом и состоит задача аппроксимации.
Из курса математики известно, что любая функция может быть описана сколь угодно точно бесконечным степенным рядом вида:
i(t) = а0 + а1u + а2u2 + а3u3 + . . . + аnun + . . . . (2.3)
Задача аппроксимации сводится к определению значений коэффициентов полинома, которые являются производными крутизны.
а0 =S0 ; а1=S/ ; а2 = 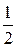 S // ; а3 =
S // ; а3 = 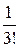 S/// ; . . . ; аn =
S/// ; . . . ; аn = 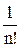 S(n).
S(n).
В различных практических задачах требуется разная точность расчетов. Часто многочлен достаточно ограничить двумя-тремя первыми членами.
i(t) = а0 + а1u + а2u2 . (2.4)
В зависимости от цели исследования цепи можно пользоваться укороченным рядом, используя только квадратичный член, отражающий наименьшие нелинейные эффекты. В некоторых задачах используют укороченный многочлен третьей степени:
i(t) = а0 + а3u3;
i(t) = а0 + а1u + а3u3. (2.5)
Порядок вычислений. Аппроксимирующая и аппроксимируемая зависимости приравниваются в отдельных, определенным образом специально выбранных точках, которые принято называть узловыми. В остальных точках совпадение аппроксимирующей функции с ВАХ лишь приближенное.
а) Аппроксимация полиномом первой степени.
Полином первой степени iап(t)=а0 + а1(u-u0) - используется для аппроксимации нелинейных участков, что показано на рис.2.4 для проходной статической ВАХ полевого транзистора (ПТ) с управляющим p-n переходом и каналом n-типа.
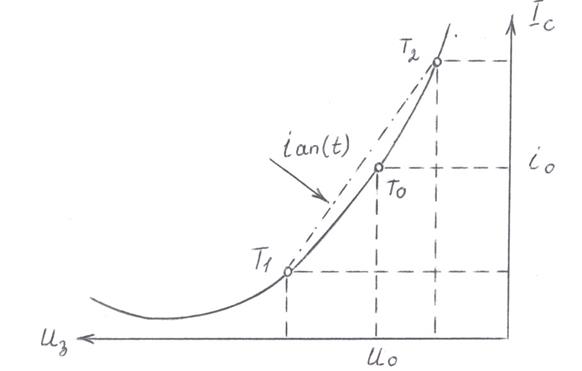
Рис.2.4. Аппроксимация ВАХ полиномом первой степени.
В уравнении два неизвестных коэффициента а0 и а1. Для их определения необходимо, чтобы аппроксимирующая прямая iап(t)=а0 + а1u (Е0=0) проходила через точку с координатами (i=i0 и u=u0) и имела крутизну линейного участка характеристики. Это, согласно определению, статическая крутизна S=S0.
Для определения коэффициентов аппроксимирующей функции получим два уравнения:
i0=а0 + а10,
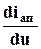 = S =
= S = 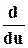 (a0 + a1u).
(a0 + a1u).
Отсюда имеем:
а0 =i0 ; а1= S и ток равен: iап(t) = i0 + S0 u.
б) Аппроксимация полиномом второй степени
Полином второй степени iап(t) = а0 + а1(u-u0) + а2(u-u0)2.
Этот полином позволяет учесть нелинейность начального участка ВАХ., что показано на рис.2.5 для полевого транзистора (ПТ) со структурой металл-диэлектрик-полупроводник (МДП-структура) с собственным каналом n-типа.
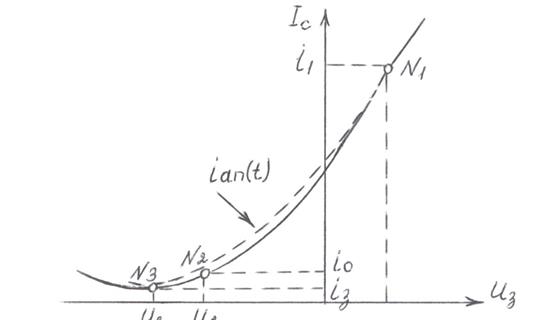
Рис.2.5. Аппроксимация начального участка ВАХ
Для определения аппроксимирующих коэффициентов а0, а1 и а2 необходимо, чтобы iап(t) совпала с i в трех узловых точках:
N1 (u=u1; i=i1); N2 (u=u2; i=i2); N3 (u=u3; i=i3).
Тогда имеем систему уравнений:
i1 = а0 + а1(u1-u0) + а2(u2-u0)2
i2 = i0 = а0
i3 = а0 + а1(u3-u0) + а2(u3-u0)2
Решение этой системы трех уравнений дает значения коэффициентов.
Аппроксимация характеристик НЭ степенными полиномами широко применяется как наиболее общий, универсальный метод. Повышение степени аппроксимирующего полинома позволяет повысить точность расчетов. Таким образом, в каждом конкретном случае можно использовать определение коэффициентов с требуемой точностью.
Выбор количества членов и степени полинома зависит от типа ВАХ. Так для туннельного диода можно использовать только полиномы нечетных степеней, начиная с третьей. Характеристика большинства специальных диодов имеет перегиб, т.е. является нечетной функцией. Практически установлено, что аппроксимация полиномом одиннадцатой степени дает расхождение iап(t) от i(t) не более 3%.
ВЫВОДЫ:
1. Аппроксимация степенным полиномом дает возможность опре-
делить коэффициенты (производные крутизны) с необходимой точностью.
2. В зависимости от типа ВАХ выбирается четная или нечетная
функция для аппроксимации: силовые диоды, транзисторы и лампы позволяют использовать полиномы второй степени.
3. Для вычисления коэффициентов полинома составляются уравне-
ния реакции НЭ для нескольких специально выбранных точек.
2.3. Аппроксимация других видов.
Наиболее часто также применяется на практике аппроксимация экспоненциальной функцией и отрезками прямых.
а) Аппроксимация экспонентой.
Наиболее подходит этот метод для ВАХ силового, туннельного или специального диода. Её представляют функцией:
iап(t) = iап(u) = АeВu .
Для двух произвольных узловых точек на ВАХ получим:
i1 = iап1(u1) = А eВu1 ,
i2= iап2(u2) = АeВu2 .
Возьмем отношение этих токов:
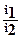 = eВ(u1-u2), откуда В=(
= eВ(u1-u2), откуда В=( 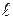 n i1 -
n i1 - 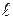 ni2) /( u1- u2).
ni2) /( u1- u2).
Затем по формуле для любого из токов i1 или i2 вычисляют коэффициент А.
Аналогично можно провести аппроксимацию функцией
iап = А( ue-Вu – 1), (2.6)
где коэффициент А выражает постоянную составляющую тока. На графике это соответствует параллельному переносу экспоненты вдоль оси ординат.
б) Аппроксимация отрезками прямых линий
Применяя для аппроксимации ВАХ многочлен первой степени, фактически полностью заменяют всю характеристику прямой линией, не принимая во внимание некоторые нелинейные участки при очень малых и очень больших напряжениях (токах). Этот метод – линейная аппроксимация – дает недостаточно точные результаты для динамического диапазона, при котором велики токи и напряжения.
Несмотря на указанный недостаток, метод линеаризации ВАХ широко используется для расчета параметров усилителей класса А, в которых рабочий участок НЭ не выходит за пределы точек А и Б рис.1.1.
Однако, в существенно нелинейных приборах не допустимо столь грубое приближение аппроксимирующей функции к реальной ВАХ.
Большую точность можно получить, если аппроксимировать характеристику нелинейного элемента несколькими отрезками прямых линий.
Как правило, аппроксимацию одного и того же типа необходимо произвести как для входных, так и для выходных и управляющих характеристик нелинейного элемента. Часто аппроксимируют только рабочий участок, а не характеристику полностью.
В простейшем случае методом линеаризации определяют параметры только двух участков ВАХ, а в общем случае можно определять параметры любого количества участков (линейно-кусочная аппроксимация). Чем больше количество участков, тем выше точность аппроксимации.
Рассмотрим это на простейшем примере аппроксимации двумя отрезками прямых управляющей ВАХ полевого транзистора с индуцированным каналом n-типа – рис.2.6.
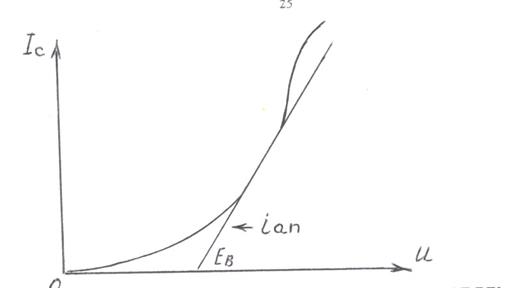
Рис.2.6. Аппроксимация двумя отрезками прямых
Как следует из рис.2.6 аппроксимирующая функция имеет вид:
iап = 0 при U<E  и U=E
и U=E  ;
; 
iап = S (U-E  ) при U>E
) при U>E  ,
,
где:
S - крутизна наклонного (прямолинейного) участка;
E  - напряжение отсечки или запирания.
- напряжение отсечки или запирания.
Коэффициенты аппроксимации определяются непосредственно по характеристике.
Аналогично для выходных ВАХ того же ПТ (рис.2.7.)
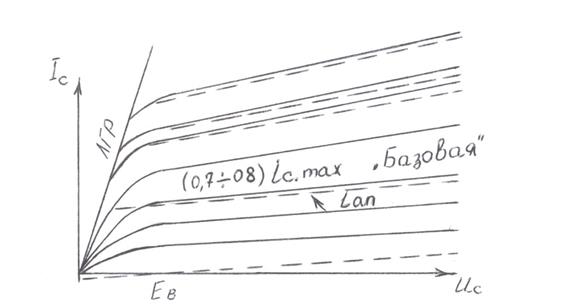
Рис.2.7. Аппроксимация выходных ВАХ ПТ
В области малых напряжений на стоке (UС от 0 до UС.min) стоковый ток iС почти не зависит от напряжения на затворе. Поэтому в этой области ВАХ аппроксимируют прямой называемой линией граничного режима (ЛГР). Она проводится из начала координат в точку максимального перешиба характеристики, соответствующей максимальному току, при котором будет работать ПТ.
Уравнение этой прямой:
iап.С = Sгр UС,
где
Sгр= 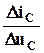 - крутизна ЛГР (граничная крутизна) определяется по графику.
- крутизна ЛГР (граничная крутизна) определяется по графику.
Правее ЛГР выходной ток ПТ (iС ) является линейной функцией двух переменных: напряжения стока UС и напряжения затвора UЗ. Она имеет вид:
iап.С = АUЗ + ВUС+С, (2.7)
где:
А, В - коэффициенты, с размерностью крутизны;
С - коэффициент, имеющий размерность тока.
Реальные характеристики заменяются семейством параллельных прямых, отстоящих на одна от другой на равных расстояниях при одинаковых приращениях напряжения на затворе. Наклон их определяется наклоном «базовой» характеристики, соответствующей (0,7-0,8) iС.max.
«Базовая» характеристика спрямляется до линии граничного режима, а все остальные проводятся параллельно ей. Расстояние между ними выдерживается равными интервалу между «базовой» и соседними ней характеристиками.
Определим коэффициенты А, В, С в выражении (2.7).
Так как крутизна S = 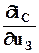 (при UС = const)
(при UС = const)
и внутреннее сопротивление R 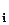 =
= 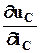 ( при UЗ = const), то из (2.7) получим: А= S , В = 1/ R
( при UЗ = const), то из (2.7) получим: А= S , В = 1/ R 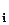 .
.
Тогда выражение для тока стока:
iап.С = S UЗ + UС /R 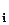 + С. (2.8)
+ С. (2.8)
Если UЗ = ЕЗ  , где ЕЗ
, где ЕЗ  - напряжение запирания, то, согласно рис.2.7 i.С= 0; UС=ЕС. Откуда получим:
- напряжение запирания, то, согласно рис.2.7 i.С= 0; UС=ЕС. Откуда получим:
С = -( S ЕЗ  + ЕЗ /R
+ ЕЗ /R 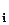 ). (2.9)
). (2.9)
Подставим (2.8) и (2.9) в (2.7) и получим:
iап.С = S [UЗ – ЕЗ  +
+ 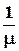 (UС-EС)]. (2.10)
(UС-EС)]. (2.10)
Это и есть аппроксимирующая функция правее ЛГР, в которой:
S - крутизна управляющей характеристики;
ЕЗ  - напряжение отсечки стокового тока, соответствующее характе-
- напряжение отсечки стокового тока, соответствующее характе-
ристике пересекающей ось абсцисс в точке UС=ЕС (i.С= 0);
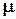 = SR
= SR 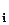 - статический коэффициент усиления.
- статический коэффициент усиления.
Дифференциальные параметры: S, ЕЗ  , R
, R 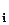 и
и 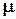 - определяются графически.
- определяются графически.
Полное выражение аппроксимированных выходных характеристик имеет вид:
0 при UС<0
iап.С Sгр UС на ЛГР
S[UЗ - ЕЗ  +
+ 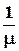 (UС-EС)] правее ЛГР.
(UС-EС)] правее ЛГР.
ВЫВОДЫ:
1. Аппроксимация нелинейного режима работы достаточно точно
осущеществляется одной экспоненциальной функцией, суммой двух экспонент или суммой прямой линии с экспонентой.
2. Линеаризация ВАХ применяется в двух вариантах: замена ха-
рактеристики двумя отрезками прямых линий и линейно-кусочная ап-роксимация несколькими отрезками прямых.
3. Коэффициенты аппроксимирующих прямых и параметры НЭ определяются графически.
ГЛАВА 3. АНАЛИЗ РЕЖИМОВ РАБОТЫ НЕЛИНЕЙНОГО ЭЛЕМЕНТА .
Целый ряд радиотехнических каскадов и, в первую очередь, усилители мощности работают в динамическом нелинейном режиме большого сигнала или же в режиме с отсечкой тока. Последний позволяет существенно повысить КПД устройства, однако приводит и к возрастанию амплитуд высших гармоник выходного сигнала, т.е. к возрастанию нелинейных искажений по сравнению с режимом без отсечки тока. Выдающийся советский ученый А.И.Берг в 30-х годах ХХ века разработал метод расчета каскадов, работающих в режиме с отсечкой тока. Этот метод широко применяется и в настоящее время как для расчетов ламповых, так и транзисторных каскадов. Рассмотрение угла отсечки позволяет усвоить основы этого метода. Кроме того, в процессе вычисления параметров по методу А.И.Берга анализируются особенности работы НЭ, имеющие большое значение при выборе области применения данного нелинейного элемента.
При изучении методов расчета режима, использующих тот или иной вид аппроксимации статических вольт-амперных характеристик, следует уделить внимание следующим вопросам:
1. Как с необходимой точностью выбрать аппроксимирующую
функцию?
2. Как графически выполнить построение рабочего участка и вы-
брать точку покоя для осуществления расчетного режима работы НЭ?
3. Каким способом определяются коэффициенты аппроксими-
рующей функции по заданным вольт-амперным характерситикам?
4. Как проверить степень точности аппроксимации?
3.1. Работа без отсечки тока
В этом динамическом режиме работы входное напряжение имеет большие амплитуды, вследствие чего рабочий участок охватывает существенно нелинейные области ВАХ. Форма сигналов при этом искажается – рис.2.1. Режим работы не моногармоничекий. Воздействие с одной (основной) гармоникой на входе приводит к появлению высших гармоник на выходе. Задача расчета заключается в определении амплитуд гармоник, имеющих значение для работы прибора. Такой расчет называется гармоническим анализом, использующим разложение в ряд Фурье как воздействия, так и реакции НЭ.
Из математики известно, что если периодическая функция удовлетворяет условиям Дирихле, т.е она непрерывна, монотонна и имеет производные высших порядков в данном интервале, то её можно представить функциональным рядом Фурье. Для переменной составляющей выходного тока НЭ он имеет вид: 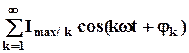 ,
,
где:
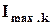 - амплитуда k-той гармоники; k
- амплитуда k-той гармоники; k 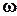 - частота k-той гармоники;
- частота k-той гармоники;
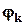 - начальная фаза k-той гармоники.
- начальная фаза k-той гармоники.
В динамическом режиме рабочий участок имеет нелинейные части, ток, протекающий через НЭ, выражается суммой ряда и постоянной составляющей:
i(t) = I0 + Imax.1 cos  t+Imax.2cos2
t+Imax.2cos2  t +Imax.3cos3
t +Imax.3cos3  t +. . .+,
t +. . .+,
где для простоты опущены начальные фазы гармоник.
Аналогично можно представить многочлен аппроксимирующей функции тока, если на вход воздействует косинусоидальное напряжение: iап(t) = а0 + а1(u-u0) + а2(u-u0)2 + а3(u-u0)3 +. . .
Заменим разность напряжений его гармоническим выражением:
iап (t) = а0 + а1 Umaxcos  t + а2(Umaxcos
t + а2(Umaxcos  t )2 + а3(Umaxcos
t )2 + а3(Umaxcos  t)3 +. . .
t)3 +. . .
Возведем в необходимые степени, после чего воспользуемся тригоно-метрическими соотношениями:
cos2  t =
t = 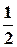 (1+ cos2
(1+ cos2  t);
t);
cos3  t =
t = 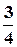 cos
cos  t +
t + 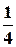 cos3
cos3  t;
t;
cos4  t =
t = 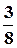 +
+ 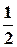 cos2
cos2  t +
t + 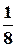 cos4
cos4  t и так далее.
t и так далее.
После всех преобразований получим:
iап (t) = (а0 + 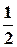 а2 U
а2 U 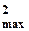 +
+ 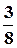 а4 U
а4 U 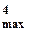 + …) +
+ …) +
+ (а1U 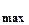 +
+ 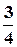 а3U
а3U 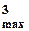 +
+ 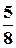 а5 U
а5 U 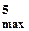 + …) cos
+ …) cos  t +
t +
+ ( 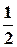 а2U
а2U 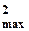 +
+ 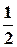 а4 U
а4 U 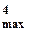 + …) cos2
+ …) cos2  t +
t +
+ ( 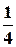 а1U
а1U 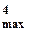 +
+ 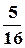 а5 U
а5 U 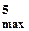 + …) cos3
+ …) cos3  t + … + =
t + … + =
= I0 + 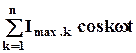 ,
,
где
I0=а0 + 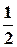 а2 U
а2 U 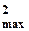 +
+ 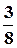 а4 U
а4 U 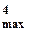 + …- постоянная составляющая;
+ …- постоянная составляющая;
Imax.1=а1U 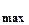 +
+ 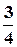 а3U
а3U 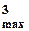 +
+ 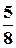 а5 U
а5 U 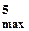 + …;
+ …;
Imax.2 = 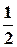 а2U
а2U 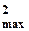 +
+ 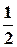 а4 U
а4 U 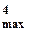 + …;
+ …;
Imax.3 = 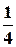 а1U
а1U 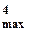 +
+ 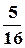 а5 U
а5 U 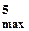 + … и т.д.
+ … и т.д.
Всего в данном ряду (разложении) будет столько гармоник кратных  , сколько степеней напряжения. Таким образом, можно выбрать степень аппроксимации. Чем больше гармоник необходимо учесть, тем выше степень аппроксимирующего полинома.
, сколько степеней напряжения. Таким образом, можно выбрать степень аппроксимации. Чем больше гармоник необходимо учесть, тем выше степень аппроксимирующего полинома.
Следует отметить, что средняя крутизна данного режима, вычисленная графически, приобретает дополнительную погрешность из-за неучета вклада высших гармоник. Анализ показывает, что величина погрешности обратно пропорциональна добротности, т.е чем выше добротность, тем меньше погрешность. Как известно, качество элемента тем лучше, чем выше его добротность.
На практике широко используются два графо-аналитических метода расчета режима без отсечки тока: трех ординат и пяти ординат.
а) Метод трех ординат
Пусть на входе НЭ, характеристика которого задана графически – рис.3.1, действует напряжение: u1 = u0 + Umax cos  t
t
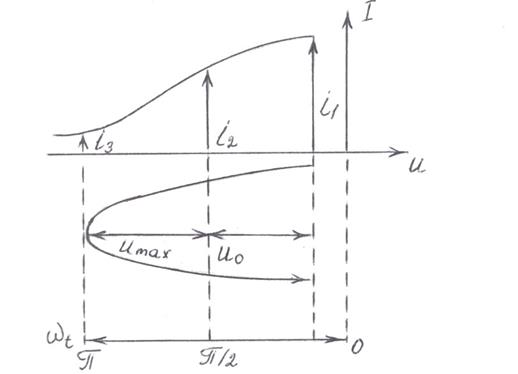
Рис.3.1. Расчет режима методом трех ординат
Пусть требуется определить постоянную составляющую I0 и амплитуду первых двух гармоник Imax.1 и Imax.2. В этом случае ряд ограничивается первыми тремя членами:
i(t) = I0 + Imax.1cos  t + Imax.2cos2
t + Imax.2cos2  t . (3.1)
t . (3.1)
Для определения трех неизвестных выберем на графике три ординаты:
i1 при 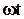 =0 U = U 0+ Um
=0 U = U 0+ Um
i2 при 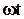 =
= 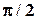 U = U 0
U = U 0
i3 при 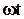 =
=  U = U 0- Um
U = U 0- Um
Подставим значения этих трех токов и соответствующие им значения аргумента в формулу (3.1)
i1 I 0+ Im1 + Im2
i2 I 0- Im2
i3 I 0- Im1 + Im2
Решая систему относительно I 0, Im1, Im2 получим формулы, известные под названием формулы трех ординат:
I 0=(i1+i3+2i2)/4;
Im1 =(i1- i3)/2;
Im2=(i1+i3-2i2)/4.
Следует отметить, что ограничение ряда Фурье первыми двумя членами приводит к ошибке в определении амплитуд гармоник, так как полином второй степени неточно отображает характеристику в заданном интервале. Если возникает необходимость определить гармоники более высоких порядков, то прибегают к более точным методам.
б) Метод пяти ординат
На рис.3.2. отмечены пять ординат этого метода, позволяющие вычислить I 0, Im1, Im2, Im3, Im4. Для каждой точки составляется уравнение тока, а затем решается полученная система из пяти уравнений с пятью неизвестными.
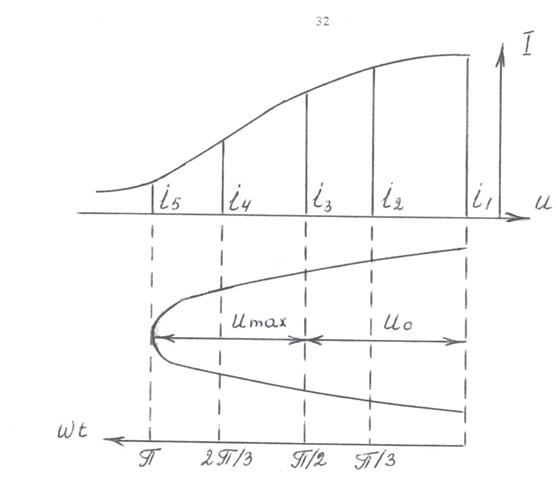
Рис.3.2. Метод пяти ординат.
i1 при 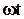 =0 U = U 0+ Um
=0 U = U 0+ Um
i2 при 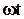 =
= 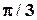 U = U 0 +
U = U 0 + 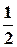 Um
Um
i3 при 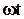 =
= 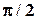 U = U 0
U = U 0
i4 при 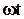 =2
=2 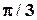 U = U 0 -
U = U 0 - 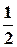 Um
Um
i5 при 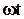 =
=  U = U 0- Um
U = U 0- Um
Решение системы дает формулы пяти ординат:
I 0=[i1+i5+2(i2+ i4)]/6;
Im1 =(i1- i3 + i2 - i4)/3;
I m2=(i1+i5-2i3)/4;
I m3=[i1-i5-2(i2-i4)]/6;
Im4 =[i1+ i5 - 4(i2+ i4) +6i3]/12.
Методы: трех и пяти ординат очень просты и применяются часто для оценки нелинейности в усилителях. Однако, при сильной нелинейности точности этих методов не достаточно. Для большей точности используют коэффициент гармоник:
КГ = 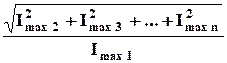 .
.
Этот коэффициент показывает энергетическое соотношение вкладов высших гармоник относительно первой (основной) гармоники.
Если измерения позволяют определить только амплитуды напряжений гармоник, или мощности отдельных гармоник, то в этом случае применяются следующие формулы для вычисления коэффициента гармоник:
КГ = 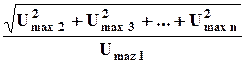 ;
;
КГ = 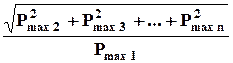 .
.
ВЫВОДЫ:
1. Для расчета динамического режима применяется гармоничес-
кий анализ, целью которого является определение амплитуд постоянной составляющей, первой и высших гармоник.
2. Большое распространение получили два графо-аналитических
метода: метод трех ординат и метод пяти ординат.
5. При высокой степени нелинейности статических ВАХ приме-
няют коэффициент гармоник, дающий большую точность вычислений.
3.2 . Анализ работы НЭ в режиме с отсечкой тока
До сих пор рассматривался такой режим работы, при котором минимальная величина воздействующего напряжения превосходила напряжение запирания (Umin>E  ). При этом ток через нелинейный элемент протекал в течение всего периода напряжения воздействия. Если же минимальная величина входного напряжения меньше напряжения запирания (Umin< E
). При этом ток через нелинейный элемент протекал в течение всего периода напряжения воздействия. Если же минимальная величина входного напряжения меньше напряжения запирания (Umin< E  ), то появляются промежутки времени, когда ток через НЭ не протекает, что показано на рис.3.3.
), то появляются промежутки времени, когда ток через НЭ не протекает, что показано на рис.3.3.
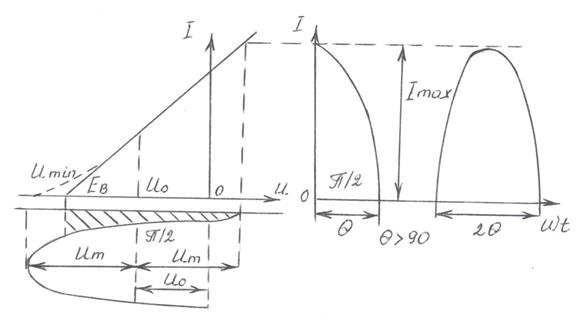
Рис.3.3. Форма сигнала в режиме с отсечкой тока
Как видно из этого рисунка, ток представляет собой последовательность импульсов.
Рассмотрим работу НЭ в режиме большого сигнала, когда статические ВАХ можно аппроксимировать отрезками прямых. Аналитическое выражение аппроксимирующей функции имеет вид:
iап = 0 при U<E  и U=E
и U=E  ;
; 
iап = S (U- E  ) при U>E
) при U>E  ,
,
а воздействующее напряжение: u = u0 + Umax cos  t .
t .
Так как воздействие периодическое, то и выходной ток (сигнал) – периодическая функция, представляющая собой последовательность косинусоидальных импульсов. Импульсы тока характеризуются двумя основными параметрами: амплитудой Imax и углом отсечки  .
.
Угол отсечки – это половина времени за период, в течение которого через НЭ протекал ток, выраженная в радианах (долях  ) или в градусах. Как видно из рис.3.3, угол отсечки – это значение аргумента
) или в градусах. Как видно из рис.3.3, угол отсечки – это значение аргумента
Выходного сигнала, отсчитываемое от момента, когда выходной ток достигает максимума до момента, когда ток становится равным нулю («отсекается» при воздействующем напряжении равном напряжению запирания).
При 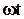 =
=  u = E
u = E  .
.
При этом напряжение принимает вид: E  = u0 + Umax cos
= u0 + Umax cos  ,
,
откуда cos  =
= 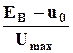 , (3.2)
, (3.2)
Дата добавления: 2018-05-10; просмотров: 2843;











