Однородные уравнения второй степени.

I. Однородное уравнение второй степени

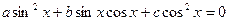, где ,

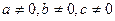делится на 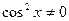либо на 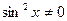и приводится к квадратному уравнению

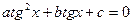или ,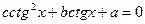

которые решаются методом замены переменной, полагая 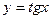или .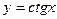

II. Если 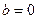, , 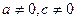уравнение имеет вид:

,

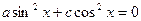уравнение делится на 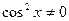либо на 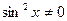и приводится к виду:

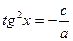или .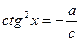

III. Если 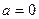, , 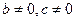уравнение имеет вид:

.

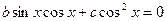Решается методом разложения на множители, и сводится к решению простейшего тригонометрического уравнения и однородного уравнения первой степени:

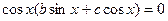
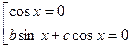
IV. Если 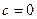, , 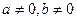уравнение имеет вид:

.

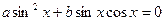Решается аналогично случаю III:

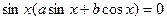
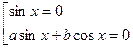
Пример.Решите уравнение

.

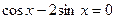Решение

Разделим на 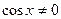обе части уравнения (т.к. 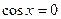не является решением уравнения, то без потери корней можем считать ):

; ; .

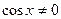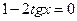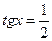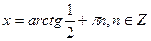Ответ: .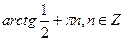

Пример.Решите уравнение

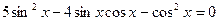
Решение.

Разделив обе части уравнения на 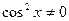, получим уравнение:

.

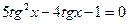Замена: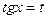

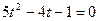
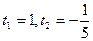
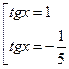
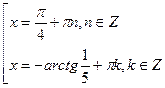
Ответ: , .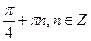

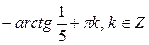Линейные неоднородные тригонометрические уравнения

Определение.Уравнение вида 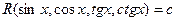, где 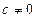, называется неоднородным тригонометрическим уравнением.

Рассмотрим методы решения таких уравнений.