Уравнения, решаемые с помощью формул понижения степени
Метод разложения на множители
Метод разложения на множители заключается в следующем: если
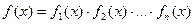 ,
,
то всякое решение уравнения
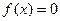 (1.1)
(1.1)
является решением совокупности уравнений:
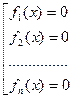 (1.2).
(1.2).
Обратное утверждение, неверно: не всякое решение совокупности уравнений (1.2) является решением уравнения (1.1). Это объясняется тем, что решения отдельных уравнений совокупности (1.2) могут не входить в область определения функции 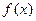 . Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.
. Поэтому, при решении тригонометрического уравнения необходимо учитывать область допустимых значений исходного уравнения и выбирать только те корни, которые в нее входят.
При решении тригонометрических уравнений с помощью разложения на множители очень часто необходимо преобразовать сумму или разность тригонометрических функций в произведение.
Пример. Решите уравнение
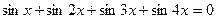 .
.
Решение.
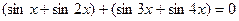
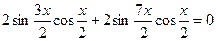
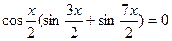
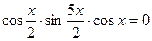
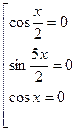
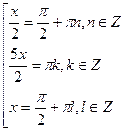
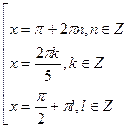
Ответ: 
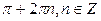 ;
; 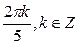 ;
; 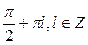 .
.
Метод замены переменной
Данный метод позволяет с помощью введения новой переменной, свести решение тригонометрического уравнения к решению алгебраического уравнения.
Пример.Решите уравнение
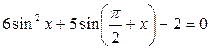
Решение.
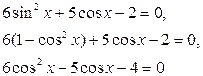
Замена: 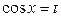 ,
, 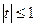
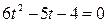
t1 = -1/2, t2=4/3
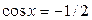
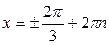 ,
, 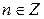 .
.
Ответ: 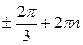 ,
, 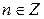
Уравнения, решаемые с помощью формул понижения степени
Решение многих тригонометрических уравнений, содержащих функции в четных степенях, основано на применении формул понижения степени:
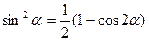
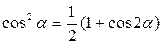
Очень часто эти формулы применяются в виде:
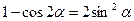
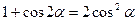
Пример.Решите уравнение
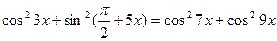 .
.
Решение

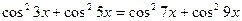
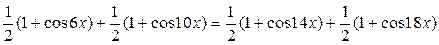
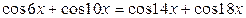
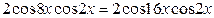
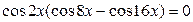
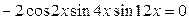
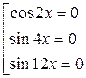 ;
; 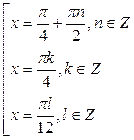 ;
; 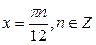
Ответ: 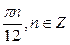 .
.
Дата добавления: 2021-11-16; просмотров: 424;











