НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА

Упругое твердое тело представляет собой наиболее простую и широко распространенную модель твердого тела. Для таких тел характерно отсутствие остаточной деформации при снятии внешних сил. Здесь А_деф.=А_{восстан.}

Предположим, что упругое тело находится под действием внешней нагрузки. Для определения напряжений в любой точке тела вырезаем элементарный куб в окрестностях этой точки. Действие отброшенных частей тела заменяем напряжениями на гранях куба, которые разложим по направлениям осей координат.

Напряжения, перпендикулярные граням куба, называются нормальными и обозначаются s, а действующие в плоскости грани - касательными и обозначаются t с соответствующими индексами (рис.1).

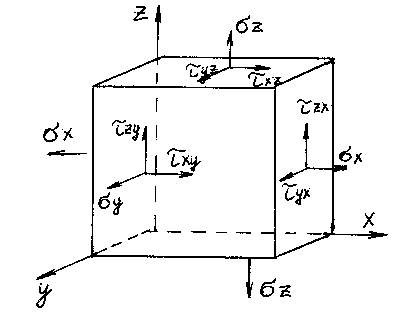
Рис.1

Схема компонент напряжений на гранях куба

Из условия равновесия элементарного куба можно записать, что t_xz=t_zx;

t_yz=t_zy;

t_xy=t_yx.

Таким образом, напряженное состояние в точке описывается шестью компонентами напряжений - s_x,s_y,s_z,t_xz, t_yz, t_xy.

Можно подобрать ориентацию граней куба так, что

t_xz=0, t_yz, =0, t_xy=0.

В этом случае соответствующие нормальные напряжения, называемые главными нормальными напряжениями, обозначаются s₁,s₂,s₃, причем s₁³ s₂ ³s₃.

Сумма нормальных напряжений, действующих по трем взаимно перпендикулярным направлениям, есть величина постоянная:

s_x+s_y+s_z = s₁+s₂ +s₃ = 3s₀,

где s₀ - среднее нормальное напряжение (гидростатическое давление в точке).

По аналогии с главными нормальными напряжениями, рассматриваются и главные касательные напряжения. Они могут быть определены по формулам:

Деформации растяжения или сжатия принято обозначать e.

Согласно закону Гука величина деформации прямо пропорциональна нормальному напряжению

,

где Е - модуль деформации при растяжении и сжатии (модуль Юнга).

Рассматриваемая же обобщенный закон Гука, можно сделать вывод, что упругое тело характеризуется модулем Юнга и коэффициентом Пуассона и что этот закон справедлив только для изотропного тела, в то время, как чаще приходится иметь дело с анизотропными телами. Это значительно усложняет их математическое описание.

Применительно к горным породам закон Гука соблюдается лишь в области малых деформаций.

Для решения большинства задач механики горных пород рекомендуется исходить из следующих общих положений:

1. Направления главных нормальных напряжений и главных деформаций удлинения совпадают.

2. Объемная деформация пропорциональна среднему номинальному напряжению и описывается уравнением

где - начальный объем элементарного куба;

- изменение объема элементарного куба под действием внешней нагрузки;

K - модуль объемной деформации;

,

где - коэффициент Пуассона

,

где - относительная поперечная деформация;

- относительная продольная деформация.

3. Главные касательные напряжения пропорциональны главным деформациям сдвига

,

где - модуль пластичности;

модуль G - деформации при сдвиге в пределах пропорциональности.