Уравнение Эйлера об изменении количества движения.
Основные уравнения движения газа в двигателях и их элементах (продолжение)
Обобщенное уравнение Бернулли
Если из уравнения сохранения энергии вычесть уравнение 1 закона термодинамики, то получим уравнение
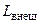 =
= 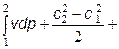 L r ,
L r ,
которое и называется обобщенным уравнением Бернулли. Оно, как уже отмечалось при изучении термодинамики газовых потоков, отличается от известного в гидродинамики уравнения Бернулли учетом наличия внешней работы и гидравлических сопротивлений.
При этом интеграл 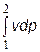 называется работой сжатия газа в потоке, причем слова ²в потоке² обычно опускаются. Таким образом, согласно обобщенному уравнению Бернулли внешняя работа, подведенная к газу в потоке, расходуется на работу сжатия газа, на изменение (увеличение) его кинетической энергии и на работу по преодолению гидравлических потерь.
называется работой сжатия газа в потоке, причем слова ²в потоке² обычно опускаются. Таким образом, согласно обобщенному уравнению Бернулли внешняя работа, подведенная к газу в потоке, расходуется на работу сжатия газа, на изменение (увеличение) его кинетической энергии и на работу по преодолению гидравлических потерь.
Уравнение Эйлера об изменении количества движения.
При проектировании газотурбинных двигателей, анализе их рабочего процесса и расчете эксплуатационных характеристик возникает необходимость определения сил взаимодействия газа с элементами двигателя, находящимися в потоке.
Например, при определении усилий, действующих на лопатки компрессора и турбины, силы тяги, создаваемой двигателем, и в других случаях.
Рассмотрим аэродинамический профиль, обтекаемый потоком.
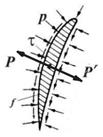
Вектор аэродинамической силы 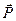 , действующей на этот профиль, можно определить, интегрируя силы давления
, действующей на этот профиль, можно определить, интегрируя силы давления 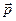 и трения
и трения 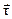 [Н/м2], с которыми газ действует на поверхность f этого профиля. Тогда
[Н/м2], с которыми газ действует на поверхность f этого профиля. Тогда
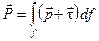 .
.
Очевидно, что профиль воздействует на газ с силой 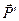 , равной по величине, но противоположно направленной, т.е.
, равной по величине, но противоположно направленной, т.е. 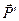 = –
= – 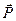
Однако определение силы 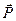 интегрированием сил давления и трения газа в инженерной практике затруднительно, т.к. значения этих сил по поверхности обтекаемого тела очень сложно рассчитать.
интегрированием сил давления и трения газа в инженерной практике затруднительно, т.к. значения этих сил по поверхности обтекаемого тела очень сложно рассчитать.
Если использовать теорему Эйлера об изменении импульса газового потока при обтекании тела, то аэродинамическую силу, действующую на тело, можно определить без знания 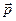 и
и 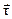 во всех точках обтекаемой поверхности. И это намного проще, чем интегрирование.
во всех точках обтекаемой поверхности. И это намного проще, чем интегрирование.
Как известно из курса физики, импульсом тела называется произведение его массы на его скорость. В теории авиационных двигателей для аналогичной величины применительно к потоку газа используется термин ²количество движения². Это термин мы и будем использовать в дальнейшем.
Для вывода уравнения Эйлера используем известный из механики 2-й закон Ньютона. Согласно ему равнодействующая всех внешних сил, действующих на тело, равна произведению массы тела на его ускорение:
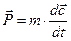
Примем, что движение газа установившимся. Выделим произвольной поверхностью F некоторый объем газа, окружающий обтекаемое тело, например, профиль. (Такую поверхность обычно называют ²контрольной поверхностью²)
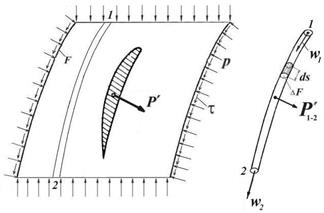
Выберем в этом объеме произвольную трубку тока 1-2 и разобьем ее на элементарные частицы с массами dm = ρΔFds, где ρ – плотность газа, ΔF – площадь поперечного сечения трубки тока, s – криволинейная координата вдоль трубки тока, отсчитываемая от ее начала (сечения 1), а ds – элемент этой координаты. Массовыми силами, действующими на газ, будем пренебрегать, так как они (например, сила тяжести) несоизмеримо малы по сравнению с аэродинамическими силами, действующими на воздух или продукты сгорания в двигателе.
Согласно 2 закона Ньютона, для каждой такой элементарной частицы можно записать
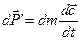 (1.1)
(1.1)
где 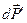 - равнодействующая внешних сил, действующих на элементарную частицу газа с массой dm,
- равнодействующая внешних сил, действующих на элементарную частицу газа с массой dm, 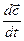 - ускорение этой частицы. Тогда
- ускорение этой частицы. Тогда 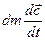 – ее сила инерции.
– ее сила инерции.
Так как при установившемся движении скорость в каждом сечении трубки тока не зависит от времени, то производная скорости по времени может быть представлена как
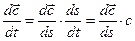
Подставив значение dm и 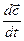 в равенство (1.1) и проинтегрировав его вдоль трубки тока, получим
в равенство (1.1) и проинтегрировав его вдоль трубки тока, получим
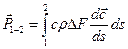 (1.2)
(1.2)
Но в равенстве (1.2) 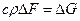 – расход газа через трубку тока, одинаковый в каждом ее сечении, а
– расход газа через трубку тока, одинаковый в каждом ее сечении, а 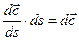 – дифференциал вектора скорости. И тогда
– дифференциал вектора скорости. И тогда
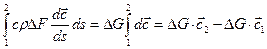
что после постановки в (1.2) дает
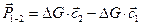 . (1.3)
. (1.3)
Формула (1.3) и представляет собой выражение теоремы Эйлера для трубки тока. Согласно этой формулепри установившемся течении газа и отсутствии массовых сил равнодействующая всех газодинамических сил (сил давления и трения), приложенных к поверхности отрезка трубки тока 1–2, включая ее торцы, равнаежесекундному изменению импульса (количества движения) протекающего через данную трубку тока газа.
Распространим далее полученный результат на всю массу газа, выделенную контрольной поверхностью F. Разобьем мысленно занимаемый ею объем на множество трубок тока, включая и прилегающие к обтекаемой поверхности профиля, и просуммируем выражения (1.3), записанные для каждой из них. При таком суммировании гидродинамические силы, действующие на струйки тока внутри контрольной поверхности, взаимно компенсируются, так как силы, действующие на каждый элемент поверхности соседних струек одинаковы по величине и противоположны по направлению. Неуравновешенными при суммировании останутся силы давления и трения, действующие снаружи на массу газа, выделенную контрольной поверхностью F (обозначим их сумму, полагая площадь сечения каждой трубки тока бесконечно малой, как 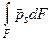 ) и сила
) и сила 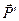 , действующая на газ со стороны профиля, находящегося в выделенном контрольной поверхность объеме газа.
, действующая на газ со стороны профиля, находящегося в выделенном контрольной поверхность объеме газа.
Количества движения 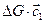 и
и 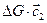 каждой трубки тока просуммируются при этом по всей контрольной поверхности F. Тогда получим
каждой трубки тока просуммируются при этом по всей контрольной поверхности F. Тогда получим
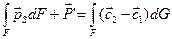
Таким образом, при установившемся течении газа сумма всех гидродинамических сил (сил давления и трения), действующих на выделенную произвольной контрольной поверхностью F массу газа со стороны контрольной поверхности и обтекаемых тел, равна разности количеств движения вытекающей из этой поверхности и втекающей в неё в единицу времени масс газа. (Это и есть теорема Эйлера о количества движения установившегося потока газа).
Аналогичным образом доказывается теорема Эйлера о моменте количества движения установившегося газового потока. Рассмотрим схему течения.
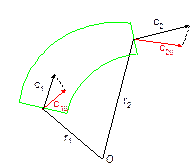 При установившемся течении газа сумма моментов всех гидродинамических сил, действующих на выделенную контрольной поверхностью F массу газа со стороны этой поверхности, относительно произвольной оси и момента сил относительно этой же оси, действующих на эту массу со стороны обтекаемых тел, равна разности моментов количеств движения вытекающей и втекающей в единицу времени масс газа относительно той же оси.
При установившемся течении газа сумма моментов всех гидродинамических сил, действующих на выделенную контрольной поверхностью F массу газа со стороны этой поверхности, относительно произвольной оси и момента сил относительно этой же оси, действующих на эту массу со стороны обтекаемых тел, равна разности моментов количеств движения вытекающей и втекающей в единицу времени масс газа относительно той же оси.
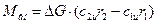
Дата добавления: 2018-05-10; просмотров: 2356;











