Реальные газы. Уравнение Ван-дер-Ваальса

Модель идеального газа (когда притяжением молекул пренебрегают) достаточно хорошо описывает поведение реальных газов в условиях, близких к нормальным. Однако при высоких давлениях и температурах, близких к абсолютному нулю, расстояния между молекулами настолько уменьшаются, что становится необходимым учитывать размеры молекул и их взаимное притяжение. Так, в 1 м³ воздуха при нормальных условиях содержится 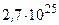молекул (число Лошмидта), занимающих объём примерно 0,1 л = 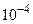м³, которым, по сравнению с объёмом газа, можно пренебречь. При давлении же в 500МПа (»1000 атмосфер) объём молекул составляет уже половину всего объёма газа.

Голландский физик Ван-дер-Ваальс в 1873 году предложил ввести в уравнение Клапейрона-Менделеева (уравнение состояния идеального газа) для 1 моля поправки: 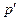- внутреннее давление газа, обусловленное взаимным притяжением его молекул, и 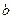-объём, занимаемый самими молекулами:

,

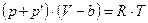где 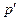= 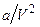, а и b-коэффициенты, характеризующие данный газ.

Тогда для произвольного количества реального газа уравнение состояния (уравнение Ван-дер-Ваальса) имеет вид:

.

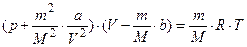Замечание: это приближённое уравнение; получены и более точные (но очень громоздкие) уравнения состояния реального газа.

Уравнение Ван-дер-Ваальса является кубическим относительно V, поэтому оно имеет три корня для V, т.е. данному значению p (при 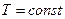) соответствуют три значения V. В зависимости от величины T эти корни могут быть либо все действительными и различными (тогда кривая 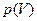имеет изгиб), либо два являются мнимыми (не соответствующими реальным состояниям системы) и только один - действительным (тогда кривая 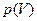монотонна).

Изотерма, соответствующая наивысшей температуре, при которой уравнение Ван-дер-Ваальса имеет три действительных значения корня для V, называется критической,а эта температура - критической температурой ( ).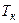

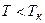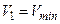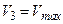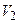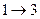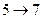Рассмотрим вначале изотерму реального газа при . В этом случае все три корня уравнения Ван-дер-Ваальса – действительные: - соответствует жидкому состоянию вещества, - соответствует газообразному состоянию, - соответствует динамическому равновесию между жидкостью и газом данного вещества. На участках и с уменьшением объёма давление растёт, что естественно. На участке 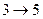сжатие вещества приводит к уменьшению давления, такие процессы в природе не осуществляются. Наличие участка 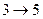означает, что при постепенном изменении объёма вещество не может оставаться всё время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы (на два агрегатных состояния). Таким образом, истинная изотерма имеет вид ломаной линии 7- 6 - 2 -1.Участок 6-7соответствует газообразному состоянию, а участок 2-1 - жидкому. В состояниях, соответствующих горизонтальному участку 6 - 2, наблюдается равновесие жидкой и газообразной фаз вещества.

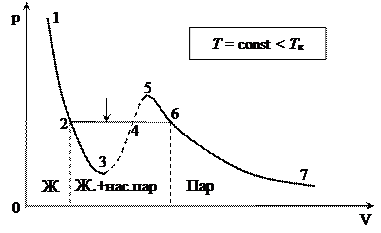Вещество в газообразном состоянии, при 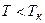, называется паром,а пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным.

Если через крайние точки горизонтальных участков семейства изотерм (соответствующих различным 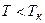) провести линию, то получится колоколообразная кривая (см. рис. на стр.84), ограничивающая область двухфазных состояний вещества.

Эта кривая и критическая изотерма делят диаграмму состояний на четыре области: под кривой располагается область двухфазных состояний (жидкость + насыщенный пар), слева от неё, при 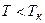, находится область жидкого состоя-

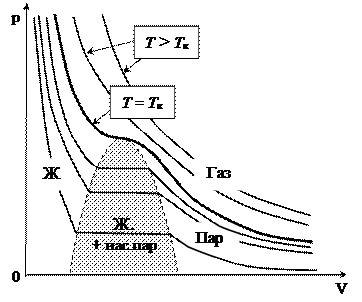ния, а справа - область пара. Пар отличается от газа тем, что при изотермическом сжатии он превращается в жидкость. При 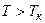, вещество может существовать только в газообразном состоянии, т.е. при 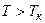вещество не может быть превращено в жидкость ни при каком давлении. Иными словами, пар – это газ, находящийся при температуре ниже критической. Отметим, что при критической температуре плотность и вязкость жидкости и газа одинаковы. Приведём значения 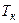для некоторых веществ: вода - 647 К, углекислота – 304 К, кислород - 154 К, воздух - 132 К, азот - 33,4 К, водород - 13,2 К, гелий -5 К.

Диффузия

Диффузия - это явление самопроизвольного выравнивания концентрации молекул данного сорта в приведённых в контакт телах. Диффузия является следствием теплового движения молекул и происходит в телах, находящихся в любом агрегатном состоянии.В отсутствие внешних сил (точнее при их взаимной компенсации)диффузия происходит до полного выравнивания концентрации молекул данного сорта по всему объёму контактирующих тел. Если же разница концентраций существует наряду с разницей температур или в условиях, когда в рассматриваемом объёме существенно изменяется сила тяжести, электрическое или магнитное поле, выравнивание концентрации необязательно. Примером может служить уменьшение плотности воздуха в атмосфере с высотой.

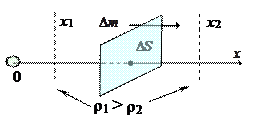Пусть в некоторой области 0 имеется неоднородность по плотности 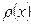. Тогда масса вещества 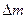, переносимого благодаря диффузии через площадку 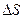, перпендикулярную оси х, вдоль которой убывает плотность r, определяется формулой Фика: 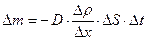, где D - коэффициент диффузии данного вещества. Знак (-) указывает на то, что перенос вещества в результате диффузии происходит в сторону убывания плотности r.

Коэффициент диффузии D численно равен массе вещества, переносимого через площадку 1 м² за 1 с при градиенте плотности 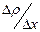= 1 кг/м⁴. Величина D зависит от природы вещества, плотности и температуры диффундирующего вещества: 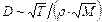(где М-молярная масса вещества). Для газов D»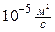, для жидкостей D»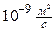, для твёрдых тел D ».

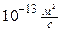Разделим обе части уравнения Фика на массу одной молекулы 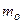. Тогда, учитывая, что 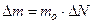и Dr = 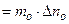(где 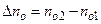- разность концентраций молекул в сечениях 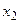и 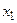), получим:

(*)

. (*)

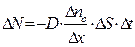
Формула (*)устанавливает связь числа продиффундировавших частиц 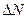с градиентом концентрации молекул 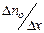вдоль оси х.

Именно диффузия обеспечивает:

1) соединение металлов при сварке, пайке, никелировании, спекании;

2) поставку растениям питательных веществ из почвы (так как концентрация полезных веществ в корнях меньше, чем в окружающей их почве);

3) поступление полезных веществ в организмы животных (через стенки желудка и кишечника организм "всасывает" только те растворённые в пище вещества, которых недостаёт для построения новых клеток).

Осмос

Это явление диффузия молекул растворителя через мембрану в раствор, в результате чего в нём возникает избыточное давление, называемое осмотическим и равное парциальному давлению растворённого вещества.

Осмотическое давление впервые исследовал в 1748 г. французский физик Ноллè в опыте с полупроницаемой мембраной из бычьего пузыря. Пузырь затягивал нижний конец воронки с водным раствором сахара, погружённой в сосуд с чистой водой. Молекулы воды могли проходить через стенки пузыря, а большие по размеру молекулы сахара - нет. Вследствие различия концентраций молекул воды в воронке и вне её, они диффундировали через мембрану в воронку. В резуль-

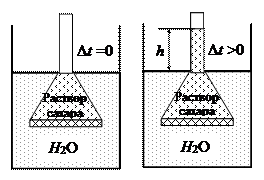тате, уровень раствора в ней повышается до значения .

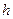Явление осмоса объяснил голландский учёный Вант-Гофф в 1887 г. Он предположил, что в слабом растворе молекулы растворённого вещества ведут себя подобно молекулам газа и поэтому такой раствор можно рассматривать как газовую смесь, подчиняющуюся закону Дальтона. Тогда в опыте Ноллè, вследствие диффузии молекул воды через мембрану в раствор, происходит увеличение объёма раствора. Это и приводит к подъёму уровня раствора в воронке на высоту 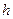, когда избыточное (по сравнению с чистой водой) давление, называемое осмотическим давлением и равное парциальному давлению молекул сахара в растворе, уравновешивается гидравлическим давлением столба жидкости.

Учитывая, что концентрация растворённого вещества 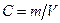(где m - масса этого вещества, 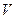- объём раствора), Вант-Гофф получил формулу для осмотического давления:

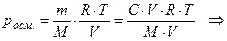
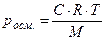
Вывод: 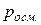не зависит от свойств растворителя.

Примеры осмоса в природе: 1) набухание сушёных ягод в воде; 2) явление тургора (упругости) биоткани; 3) осмотическое экстрагирование (извлечение) воды из биоклеток (чувство жажды после приёма сладкой или солёной пищи); 4) упругость овощей и плодов, например, у моркови осмотическое давление 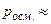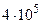Па (т.е. 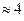атм.); 5) прорастание грибов сквозь асфальт; 6) разрушение фундаментов зданий корнями деревьев и растений.