Недостатки стандартного метода.

1) Нерационально используется площадь опытного участка, (более 50 % площади занято под контролем (стандартом).

2) Громоздкость постановки опыта. стандартные методы характеризуются большой громоздкостью и нерациональным использованием земельной площади – около 40-60 % всей площади опыта занято делянками контрольного варианта.

3) Увеличение объёмов всех выполняемых работ

4) Не всегда наблюдается тесная корреляционная зависимость между урожаями рядом расположенных делянок.

5) Очень трудно сравнивать опытные варианты, далеко расположенные друг от друга, что бывает при большом числе изучаемых вариантов.

Систематическое размещение вариантов предполагает неизменный порядок размещения вариантов на делянках, в каждом повторении опыта, порядок следования которых определяется заранее экспериментатором. Имеется много модификаций этого метода, но наиболее часто применяется последовательное (в один ярус и в несколько ярусов – шахматный) и ступенчатое размещение вариантов (рис.10).

Последовательное размещение вариантов применяется при одноярусном расположении делянок. Например, если в первом повторении опыта намечен порядок размещения вариантов схемы опыта 1, 2, 3, 4, 5, и 6, то этот же порядок сохраняется и во всех остальных повторениях.

При многоярусном расположении опытных делянок применяется ступенчатое размещение вариантов. Этот метод размещения не допускает, чтобы одноименные варианты соприкасались своими длинными или короткими сторонами. Для этого схему опыта в каждом последующем ярусе необходимо сдвинуть. Число вариантов, на которое надо сдвинуть схему опыта, определяется как результат от деления числа вариантов на число ярусов. Так, при 10-ти вариантах и трехъярусном расположении делянок схему опыта необходимо сдвигать на 3 варианта (10:3=3). В первом ярусе варианты размешаются – 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, во втором – 4, 5, 6, 7, 8, 9, 10, 1, 2, 3, в третьем – 7, 8, 9, 10, 1, 2, 3, 4, 5, 6.

Существует два способа размещения вариантов по этому методу:

а) последовательный в один ярус

б) шахматный – при размещении повторений в несколько ярусов.

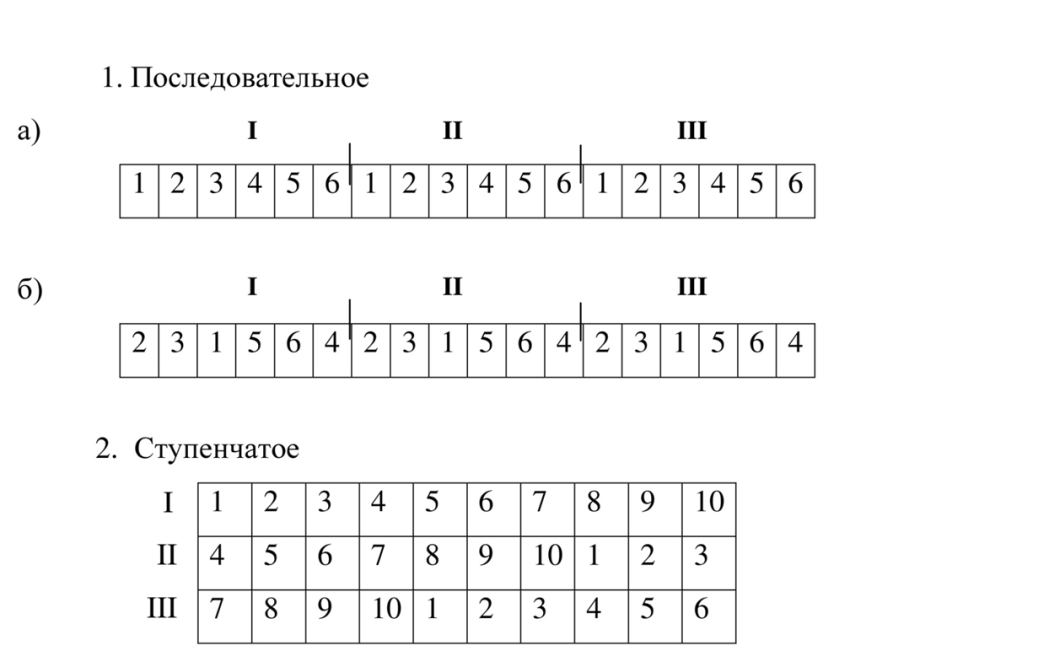
Рисунок 10 – Систематическое размещение вариантов в полевом опыте

Систематическое размещение вариантов отличается простотой, легко запомнить схему размещения вариантов на опытном участке. Первоначально этот метод занимал господствующее положение при проведении полевых опытов. Однако этот метод нельзя применять при закономерном или смешанном варьировании плодородия почвы земельного участка. Систематические методы применяются на выровненных по рельефу и плодородию участках.

Рендомизированное размещение вариантов. Рендомизация устраняет возможное одностороннее влияние закономерной изменчивости почвенного плодородия на результаты опыта. Преимущества и эффективность рендомизированного размещения вариантов убедительно доказаны Р. Фишером, Д. Снедекором, С. Пирсом, В.Н. Перегудовым, Б.А. Доспеховым и другими учеными. Рендомизация – случайное размещение вариантов по делянкам полевого опыта.

При частичной рендомизации опыты ставят методом организованных повторений. На опытном участке выделяют повторения, а внутри повторения варианты размещают рендомизированно. При этом опыт может быть поставлен: методом расщеплённых делянок или методом смешивания. Используют в опытах по сортоиспытанию, в которых изучаются много вариантов.

При полной рендомизации опыт ставят методом неорганизованных повторений. Опытный участок разбивают сразу разбивают на делянки и по ним размещают варианты рендомизированно. Применяется в отдельных случаях при закладке мелкоделяночных опытов с удобрениями, гербицидами. Такой опыт может быть поставлен методом латинского квадрата или прямоугольника.

Рендомизированный (случайный) метод размещения вариантов.

Используют три способа рендомизации.

1) С помощью карточек

2) С использованием специально разработанных схем

3) С использованием таблицы случайных чисел.

Рендомизированный метод был предложен английским учёным Фишером. Он позволяют дать более объективную оценку изучаемым вариантам и получить меньшую величину случайной ошибки.

Более современный способ рендомизации – по таблице случайных чисел. Табулированные цифры в таблице 1 сгруппированы по две. Случайность расположенных цифр – 1, 2, 3, 4, 5, 6, 7, 8, 9 заключается в том, что нет никого закона в их расположении, но каждое число встречается приблизительно одинаковое число раз. Например, планируется заложить опыт с шестью вариантами в трехкратной повторности. Обозначим варианты цифрами 1, 2, 3, 4, 5, 6 и по таблице определим порядок их размещения по повторениям. По таблице случайных чисел отметим произвольно начальный пункт отсчета и просмотрим таблицу в любом направлении до тех пор пока не получим указанный набор цифр. Предположим, что мы выбрали цифру 6 в первой строке 10 столбца. Двигаясь по этой колонке вниз, получим рендомизированное размещение для первого повторения – 6, 3, 5, 2, 1, 4. Номер последнего варианта (у нас 4) проставляют автоматически, повторяющиеся цифры и цифры, превышающие 6, пропускают. Итак, в первом повторении на первой делянке размещается вариант 6, на второй – вариант 3, на третьей – вариант 5 и т.д. Для каждого повторения рекомендуется менять точку отсчета и направление движения по таблице случайных цифр (вниз, вверх, влево, вправо, по диагонали). В итоге получен, например, такой порядок размещения вариантов по повторениям опыта: I повторение – 6, 3, 5, 2, 1, 4; II повторение – 1, 5, 3, 2, 4, 6; III повторение – 2, 3, 6, 5, 1, 4.

Рендомизация имеет ряд преимуществ перед другими методами размещения вариантов:

ü исключается субъективный подход к размещению вариантов на опытных делянках. Все варианты имеют одинаковую вероятность попасть на любую делянку опыта;

ü сводится к минимуму влияние закономерного варьирования плодородия почвы, предотвращается накопление систематических ошибок, которые, при рендомизированном размещении вариантов, превращаются в случайные;

ü разрушается возможная корреляционная связь между соседними вариантами, что делает более равноточными их попарные сравнения;

ü случайное размещение вариантов позволяет наиболее объективно использовать методы статистической обработки результатов опыта, т.к. методы вариационной статистики приложимы в полной мере только к случайным явлениям, и поэтому статистическая обработка результатов наиболее обоснованно применима при случайном размещении вариантов на делянках полевого опыта.

Рендомизированное размещение вариантов имеет несколько модификаций.

Существует два способа рендомизации:

а) с использованием частичной рендомизации

б) полная (неограниченная) рендомизация

Метод неорганизованных повторений (полная рендомизация). Варианты по делянкам опытного участка распределяются совершенно случайно. Расположение делянок может быть одно- и многоярусное.

Метод полной рендомизации рекомендуется применять при небольшом числе вариантов (3-4), когда есть основание не ставить под контроль территориальное закономерное варьирование плодородия почвы. Такие условия часто встречаются при работе с многолетними плодовыми культурами, которые характеризуются сильной индивидуальной, генетической изменчивостью Индивидуальное варьирование урожая с дерева превышает варьирование плодородия почвы.

При небольшом числе вариантов преимущество метода полной рендомизации заключается и в том, что критерий Фишера приобретает наибольшее значение по сравнению с другими методами. Максимально увеличивается число степеней свободы остаточной дисперсии, что позволяет уменьшить ошибку опыта и, следовательно, повышается его точность и статистическая достоверность. Например, при размещении четырёх вариантов при трёхкратной повторности методом полной рендомизации, число степеней свободы для остаточной дисперсии составляет: 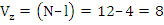при размещении вариантов методом рендомизации внутри повторений оно равно 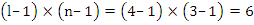, чтобы считать, что в опыте есть существенные различия в первом случае фактическое значение критерия F должно превысить F_теор. = 4,06, а во втором – 4,76.

Метод рендомизированных повторений (рендомизация внутри повторения, или рендомизация с одним ограничением) – случайное размещение вариантов схемы опыта в пределах каждого повторения. Это наиболее распространенный в мировой практике метод размещения вариантов по делянкам полевого опыта. Опытные делянки могут располагаться в один ярус и многоярусно. Рендомизация проводится отдельно по каждому повторению (рис. 11).

Рисунок 11– Размещение вариантов опыта методом рендомизированных повторений

Метод рендомизированных повторений представляет собой ортогональную схему размещения вариантов. Это означает, что в каждом повторении имеется полный набор вариантов, и каждый из них повторяется только один раз.

При постановке полевых опытов с большим числом вариантов (15-20), которые отличаются по своим морфологическим, биологическим и другим признакам (высота, скороспелость и др.), варианты внутри повторения целесообразно объединять в однородные группы. Порядок расположения групп в каждом повторении и вариантов внутри групп также определяется рендомизацией. При этом в каждой группе может быть выделен свой контрольный вариант (рис. 12).

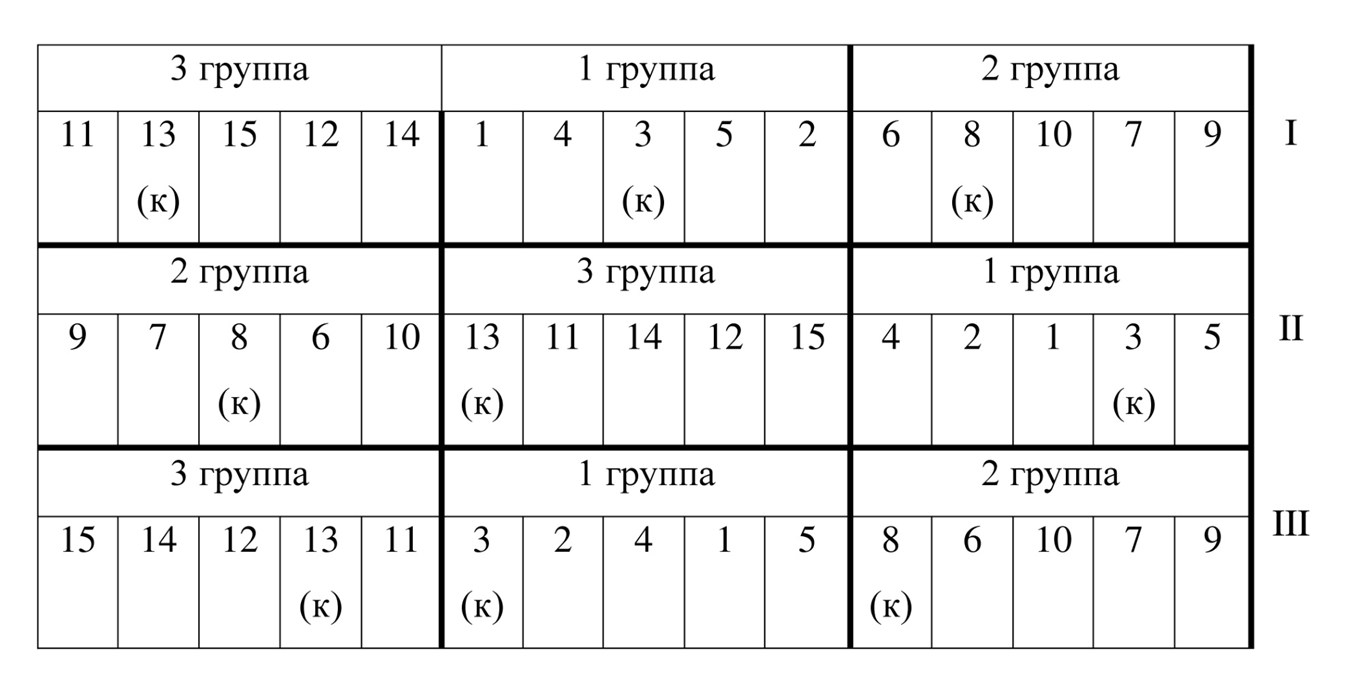
Рисунок 12 – Схема рендомизированного размещения 15 вариантов в трех повторениях, в каждом повторении по три группы

При небольшом числе вариантов и их рендомизированном размещении в одном из повторений возможно размещение вариантов систематическим методом. Это частичное отступление от строгой рендомизации не является грубым нарушением и может быть допустимо, т.к., согласно теории вероятности, такой случай размещения вариантов не исключается.

Латинский квадрат и прямоугольник (рендомизация с двумя ограничениями). Латинский квадрат и прямоугольник применяются,если плодородие почвы опытного участка изменяется в двух взаимноперпендикулярных направлениях (лесные полосы, склон и др.). Вариантыопыта располагаются по рядам и столбцам, число рядов равно числустолбцов. В каждом ряду и в каждом столбце должен быть полный наборизучаемых вариантов и, следовательно, ни один из вариантов не повторяетсядважды ни в ряду, ни в столбце. Варианты внутри столбцов и рядовразмещаются случайно. Такое расположение позволяет контролироватьизменение плодородия почвы по двум взаимно перпендикулярным направлениям и математической обработкой сэлиминировать, устранить влияние закономерного изменения плодородия почвы опытного участка на результаты опыта, повысить точность эксперимента. Размещение вариантов на делянках опыта латинским квадратом или прямоугольником способствует доказательству небольших различий между вариантами. При других методах размещения вариантов такие различия могут быть в пределах ошибки эксперимента.

Латинский квадрат применяется при числе вариантов 4-8 (рис. 13). Повторность вариантов на территории равна числу вариантов, l=n. При числе вариантов менее четырёх, нецелесообразно размещать их по методу латинского квадрата. В этом случае остаточная дисперсия 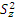опирается нанебольшое число наблюдений и становится неустойчивой базой для оценкисущественности различий между вариантами. Например, если числовариантов равно трём, то число степеней свободы для остаточной дисперсииопределяется по формуле 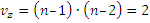. Если жеиспользовать метод полной рендомизации – 6, так как рассчитывается этотпоказатель по формуле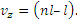

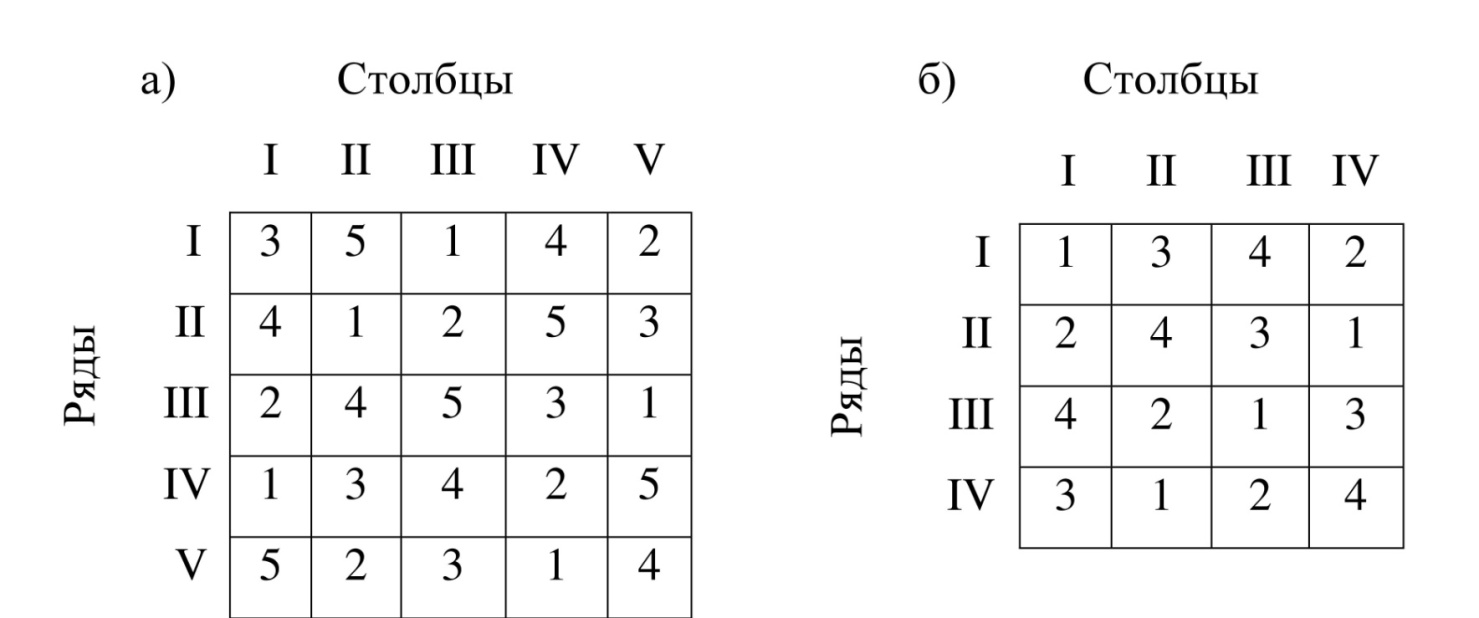
Рисунок 13– Размещение вариантов латинским квадратом: а – вариантов 5(5×5), б – вариантов 4 (4×4)

Большое преимущество латинского квадрата состоит в возможности двукратной нивелировки влияния неоднородности почвы, а именно, по рядам, столбцам. При всех остальных методах размещения вариантов, это сглаживание происходит лишь в одном направлении. С увеличением числа вариантов в схеме опыта более 5 и их рендомизированном размещении по рядам и столбцам латинского квадрата, можно воспользоваться уже разработанными схемами размещения вариантов на опытном участке (рис 14).

Рисунок 14– Схемы размещения опытов с 6-8 вариантами латинским квадратом (Б.А. Доспехов, 1985)