Требования при постановке опыта методом латинского квадрата
1. Опытный участок должен быть квадратной формы. Его разбивают на ряды и столбцы. Число их должно быть равным числу вариантов.
2. В каждом ряду и каждом столбце варианты размещаются рендомизировано.
3. Повторность опыта обязательно должна быть равна числу вариантов.(n =ℓ) ́Ν = ℓ2 . Это ограничение является недостатком латинского квадрата. Поэтому латинский квадрат используют при количестве вариантов не менее 3 и не более 8 (ℓ = 3-8).
Недостатки латинский квадрат:
1) число вариантов должно быть равно числу повторений.
2) С увеличением числа вариантов и соблюдением этого равенства, увеличивается количество опытных делянок, опыт становится громоздким при небольшой его информативности. Так, если в схеме опыта 10 вариантов, потребуется заложить 100 опытных делянок. Поэтому, считается нерациональным использование латинского квадрата при числе вариантов более 8. Отсюда, стремление найти другой метод размещения вариантов по принципу латинского квадрата, но без равенства n=l. Чтобы, не увеличивая повторности, использовать преимущество латинского квадрата, вариант опыта на опытных делянках необходимо размещать латинским прямоугольником.
Латинский прямоугольник применяется, если число вариантов больше 8 и кратно числу повторностей. При числе вариантов 9 можно заложить опыт с трёхкратной повторностью, но нельзя при четырёхкратной. Если в схеме опыта 12 вариантов, размещение вариантов латинским прямоугольником возможно при 2, 3, 4 и 6 повторностях.
В основе латинского прямоугольника лежит латинский квадрат, форма которого определяется по числу повторностей. Чтобы квадрат преобразовать в прямоугольник, необходимо число вариантов разделить на число повторностей. На полученное число расщепить каждый ряд или столбец квадрата. Например, число вариантов в схеме опыта 12, повторность – четырёхкратная, число делянок – 48. Вначале строим латинский квадрат 4×4 (рис. 15 а). Затем каждый столбец расщепляем на 3 делянки (12:4 = 3). Получаем необходимое число делянок – 48. В каждом ряду и в каждом столбце будет 12 делянок, на которых размещаются варианты опыта. Так же, как и в латинском квадрате, столбцы и ряды содержат полный набор вариантов (рис.15 б).
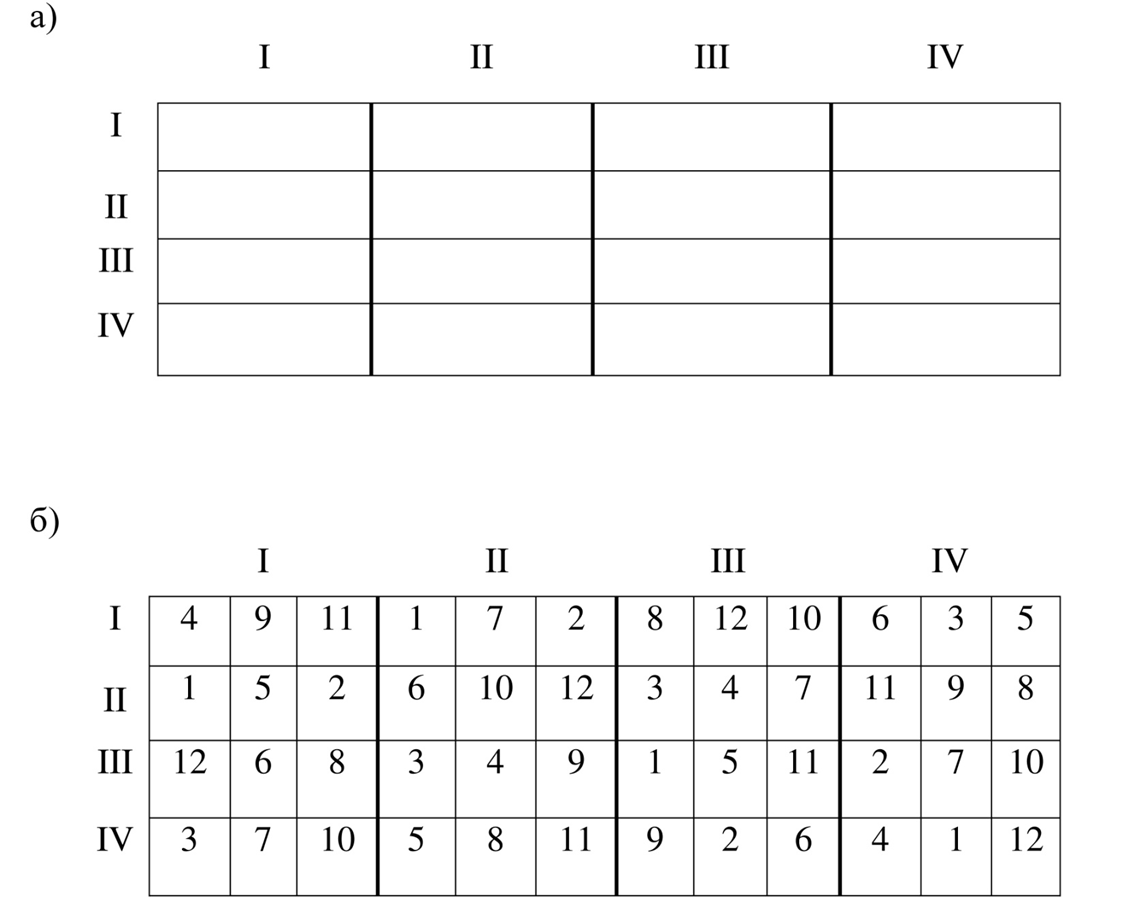
Рисунок 15 –Размещение вариантов латинским прямоугольником 4×4×3
Формула латинского прямоугольника записывается в виде произведения чисел. Например, 4×4×3, 5×5×3. Первые два множителя указывают, какой квадрат лежит в основе прямоугольника (4×4), (5×5), а третий – на сколько делянок необходимо расщепить каждый ряд, или столбец, чтобы превратить квадрат в прямоугольник. Произведение второго и третьего множителей указывает на число вариантов в схеме опыта. На рисунке 16 показаны схемы размещения опытов по методу латинского прямоугольника:

Рисунок 16 – Схемы размещения опытов с 15-20 вариантами методом латинского прямоугольника (Б.А. Доспехов, 1985)
Решетка применяется при большом числе вариантов – 25, 50 и более. Размещение полевого опыта методом организованных повторений позволяет контролировать варьирование урожайности и других наблюдений, вызванное различием плодородия между повторениями, но не учитывает территориальную неоднородность внутри их. При большом числе вариантов, когда увеличивается площадь, занятая отдельными повторениями, значительно ухудшается сравнимость вариантов.
Метод решетки, путем специального размещения вариантов, позволяет контролировать пестроту плодородия почвы не только повторения в целом, но и их отдельных его частей – блоков.
Существует много модификаций этого метода размещения вариантов.
Решетка может быть двухместная, трехместная, сбалансированная, прямоугольная и др. Наиболее простой и распространенной является простая двухместная решетка, которая характеризуется тем, что число вариантов в схеме опыта равно квадрату целого числа (16, 25, 36, 48 и т.д.). Варианты размещаются по блокам, а блоки объединяются в повторения. Число блоков в каждом повторении и число вариантов в блоке равно корню квадратному из числа вариантов 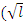 ) . Блоки в каждом повторении обозначаются римскими числами – I, II, III, IV и т.д. Простая двухместная решетка применяется при четном числе повторений. Нечетные повторения обозначаются «Х», четные – «Y». В повторении «Х» в блоках варианты размещаются по горизонтали, в повторении «Y» – по вертикали и так, чтобы варианты каждого блока повторения «Х», по одному входили во все блоки повторения «Y». На рисунке, а показано размещение по методу двухместной решетки 16 вариантов при двукратной повторности. Распределение блоков внутри повторения и вариантов внутри блока рекомендуется проводить случайно, т.е. рендомизировать (рис. 17аб).
) . Блоки в каждом повторении обозначаются римскими числами – I, II, III, IV и т.д. Простая двухместная решетка применяется при четном числе повторений. Нечетные повторения обозначаются «Х», четные – «Y». В повторении «Х» в блоках варианты размещаются по горизонтали, в повторении «Y» – по вертикали и так, чтобы варианты каждого блока повторения «Х», по одному входили во все блоки повторения «Y». На рисунке, а показано размещение по методу двухместной решетки 16 вариантов при двукратной повторности. Распределение блоков внутри повторения и вариантов внутри блока рекомендуется проводить случайно, т.е. рендомизировать (рис. 17аб).
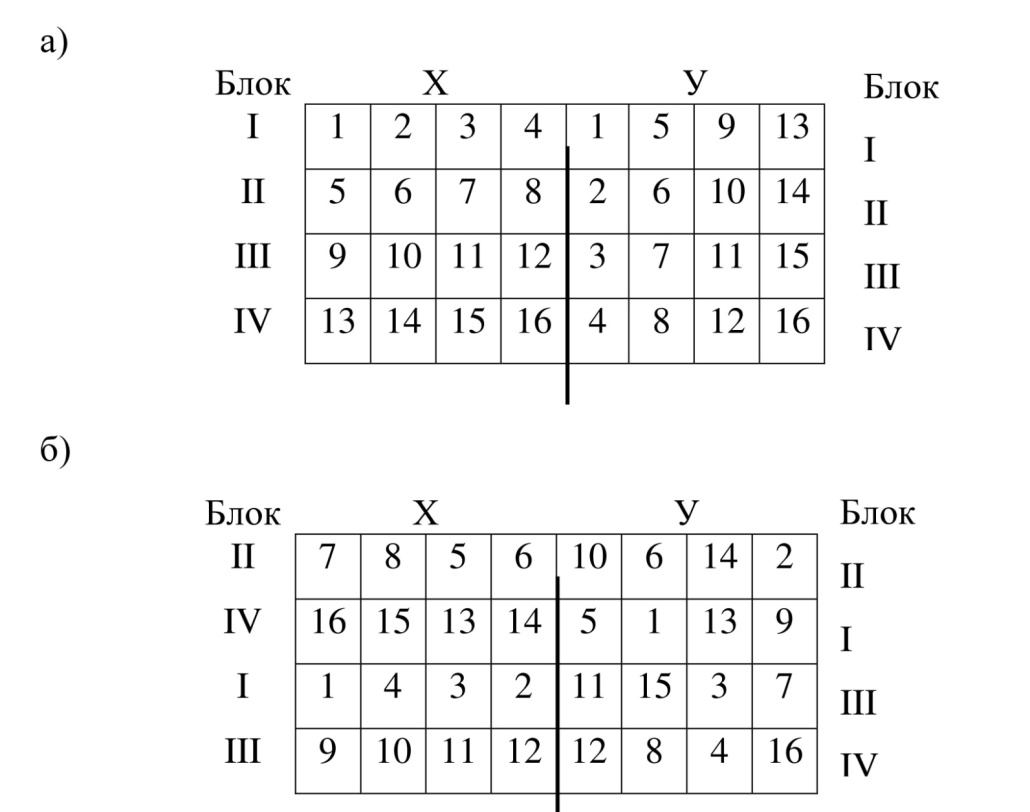
Рисунок 17 – Размещение вариантов опыта по методу решетки
Расщепленная делянка. Все ранее рассмотренные методы размещения вариантов можно применять при проведении одно- и многофакторных опытов. Размещение вариантов по методу расщепленной делянки применяется только при закладке многофакторных опытов. При таком методе размещения варианты одного фактора (делянки первого порядка), используются для размещения вариантов второго фактора (делянки второго порядка), которые потом используются для размещения вариантов третьего фактора (делянки третьего порядка) и т.д. В агротехнических опытах на делянках первого порядка целесообразно изучать приемы, которые выполняются первыми (предшественник, обработка почвы). При проведении многолетних стационарных многофакторных опытов, методу расщепленных делянок следует отдавать предпочтение. В процессе опытной работы возникают новые идеи, мысли, требующие экспериментального изучения. Метод расщепленной делянки позволяет вводить для изучения новые факторы. Для введения новых вариантов расщепляют делянки предыдущих порядков.
Делянки первого порядка называют главными делянками, а делянки второго, третьего и т. д. порядков называют субделянками. По площади, главные делянки являются самыми крупными. По мере их расщепления, площадь делянок для последующих факторов уменьшается.
Варианты по главным делянкам и субделянкам размещают методом рендомизации. Особенность их размещения в том, что варианты главных делянок рендомизируются самостоятельно по каждому повторению, варианты второго и последующих порядков рендомизируются каждый раз заново. Размещение вариантов в трехфакторном опыте 3×2×3 по изучению предшественников (а0, а1, а2), обработок почвы (в0,в1) и удобрений (с0,с1,с2) по методу расщепленной делянки показано на рисунке 18.

Рисунок 18– Размещение вариантов опыта по методу расщепленной делянки
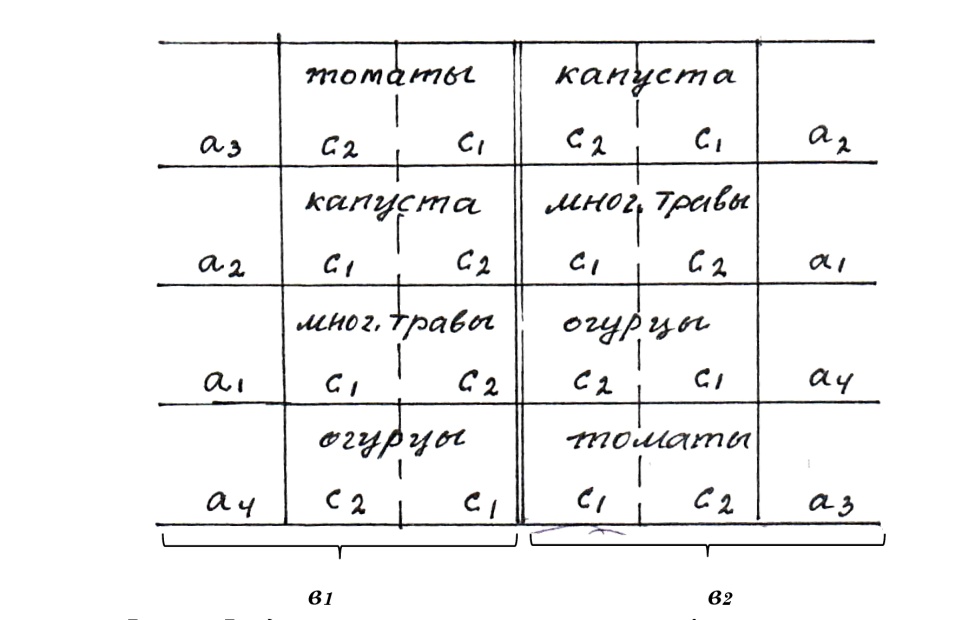
Рисунок 19 – Рендомезированное размещение трехфакторного опыта методом расщепленных делянок (в одном повторении):
а1– многолетние травы; а2 – капуста; томаты; а3– огурцы
в1 – одна норма орошения; в2 – 1,5 нормы орошения
с1 –одна норма удобрения; с2–1,5 нормы удобрения
Расщеплять опытные делянки можно в горизонтальном и вертикальном направлениях, что диктуется техническими условиями закладки и проведения полевого опыта. На рисунке 20 показано последовательное расщепление делянок в трехфакторном опыте.

Рисунок 20 – Схема последовательного расщепления вариантов в трехфакторном опыте с 24 вариантами (4×3×2)
Метод смешивания. В многофакторных опытах с увеличением числа факторов и вариантов по каждому фактору, увеличивается общее количество вариантов, для изучения которых требуется увеличение размера опытного участка. При этом из-за возможной неоднородности плодородия почвы варианты могут оказаться в неодинаковых условиях, нарушается принцип единственного различия, увеличивается ошибка, что неизбежно ведет к снижению точности исследования. Одним из эффективных приемов для снижения этих недостатков является применение при размещении вариантов метода смешивания.
Смешиванием называется такой метод размещения вариантов при котором в каждом повторении опыта варианты объединяются в группы (блоки), равноценные в отношении главных характеристик так, чтобы разности между группами составляли взаимодействие высшего порядка, представляющее меньший интерес, чем главные эффекты и взаимодействия между двумя факторами. В этом случае точность опыта определяется варьированием почвенного плодородия не по всему повторению, а внутри его части – внутри блока. Чтобы более точно сравнить варианты внутри блока, взаимодействия высшего порядка отождествляются, смешиваются с межблоковыми различиями, которые в условиях полевого опыта, как правило, не существенны и не представляют интереса.
На рисунке 21 показано размещение трехфакторного опыта по изучению удобрений: 0, N, Р, К, NР, NК, РК и NРК. Факторами здесь являются азотное, фосфорное и калийное удобрения, которые изучают в двух градациях (дозах) 0 и 1.
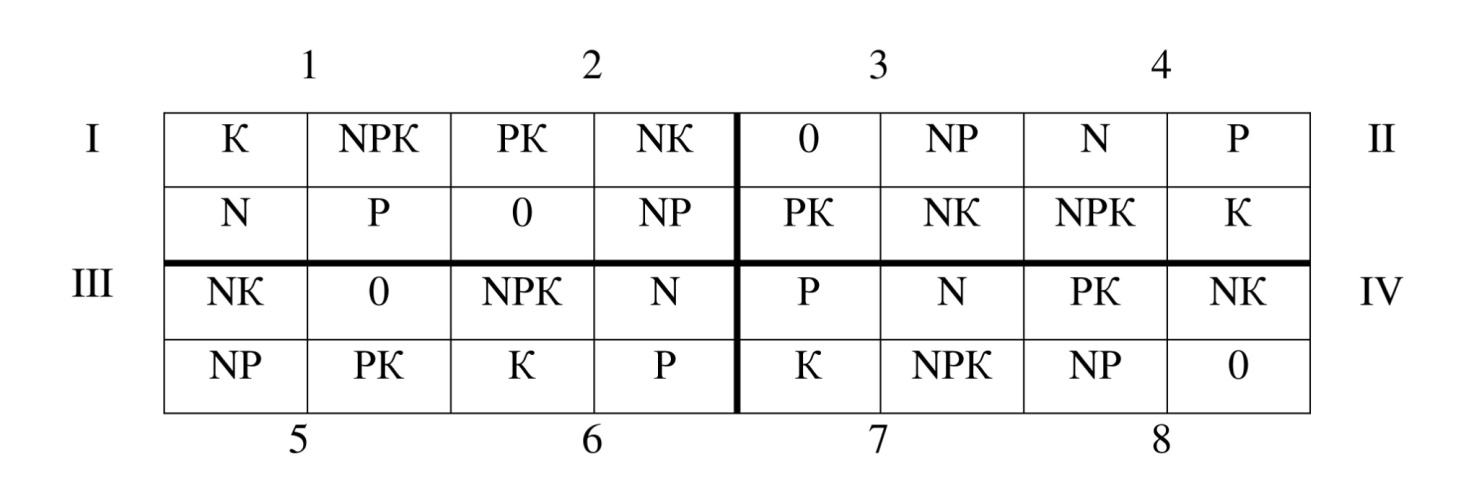
Рисунок 21 – Схема размещения трехфакторного опыта (2×2×2) методом смешивания в 8 блоках четырех повторений (смешано взаимодействие NРК)
Эффект тройного взаимодействия, которое жертвуется, определяется по формуле: (NРК) = ¼ (N+Р+К+NРК) – (0+NР+NК+РК). Если варианты N, Р, К, NРК расположить территориально в одном блоке, а варианты 0, NР, NК, РК – в другом, то тройное взаимодействие «смешивается» (отождествляется) с блоковыми различиями. Блокировка для опыта 2×2×2, в котором всего 8 вариантов, не является обязательной, но она становится необходимой, если число вариантов более 16-20 и территориальные размеры повторения становятся большими, что ведет к увеличению ошибки опыта.
Учёт урожая
Различают три метода учета урожая: сплошной, пробными площадками и снопами. В первом случае урожай с каждой учетной делянки убирают и взвешивают, а при втором методе учитывают урожай только с пробных делянок. При сноповом методе (травы, лён), учитывают биологический урожай (сырой), затем по пропорции рассчитывают товарную продукцию, семена, волокно, сено).
Дата добавления: 2018-05-10; просмотров: 5631;











