Течение в трубах неньютоновских жидкостей

Рассмотрим горизонтальную цилиндрическую трубу круглого сечения.

Аномально-вязкие жидкости.Для круглой трубы распределение напряжений трения 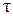определяется по формуле:

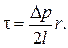
Принимая реологическое уравнение аномально-вязкой жидкости
в виде степенной зависимоcти (2.3) получим:

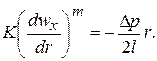(2.105)

Здесь K и m – реологические константы жидкости, Dp – потери давления на участке длиной l.

Интегрирование уравнения (2.105) при граничном условии
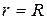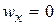, дает распределение скорости 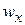по сечению трубы
в следующем виде:

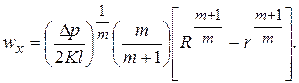(2.106)

Максимальная скорость достигается на оси трубы при 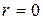. Средняя скорость получена в виде:

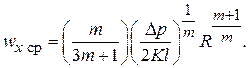(2.107)

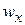Согласно формуле (2.107) потеря давления . Это означает, что Dp для псевдопластичных жидкостей растет медленнее с ростом , чем для ньютоновских, а для дилатантных – быстрее (рис. 2.33).

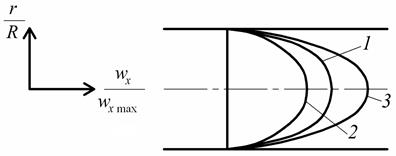
Рис. 2.33. Распределение обобщенных скоростей по сечению трубы:

1 – ньютоновская жидкость; 2 – псевдопластичная жидкость;

3 – дилатантная жидкость

Используя формулу (2.107), можно определить расход жидкости
при известных свойствах жидкости и параметрах течения. В случае необходимости из (2.107) можно найти Dp.

Вязко-пластическая среда. Эта среда обладает предельным напряжением сдвига 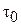. Если напряжение трения 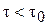, то течения среды не будет. Для реализации течения необходимо, чтобы 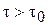(рис. 2.34).

В области 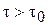возникает пристенное кольцевое течение.
В центральной части трубы, при 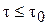среда будет двигаться как твердый стержень с одинаковой скоростью .

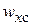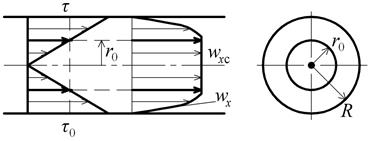
Рис. 2.34. Схема течения вязко-пластичной среды

Итак, имеем следующие исходные зависимости:

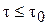
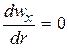При ; при 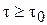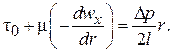(2.108)

Для кольцевой зоны получена формула:

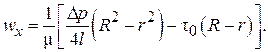(2.109)

Для осевой (стержневой) зоны:

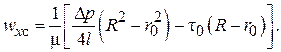(2.110)

Общий объемный расход складывается из потоков стержневой зоны 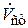и кольцевой зоны :

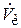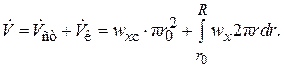(2.111)

После ряда упрощений формула (2.111) принимает вид:

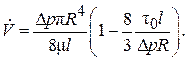(2.112)

Формула (2.112) является аналогом уравнения Пуазейля. Она может быть использована и для определения потери давления .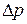

Вязко-пластические среды иногда называют бингамовскими жидкостями или телами Шведова – Бингама.