Дирекционный угол и сближение меридианов

Из-за непараллельности географических меридианов, проходящих через различные точки одной и той же прямой, азимуты, определенные в ряде точек этой прямой, не равны между собой.

Для того чтобы упростить ориентирование линий и процесс вычислений, предложено ориентирующие углы брать не от меридианов, а от направлений, параллельных какому-нибудь одному меридиану. В этом случае все ориентирующие углы одной линии в любых ее точках равны между собой (рис. 2.3). С этой целью используется осевой меридиан зоны, относительно которого в пределах зоны выполняют ориентирование направлений. Для ориентирования линий относительно осевого меридиана (оси абсцисс прямоугольной системы координат) используются дирекционные углы.

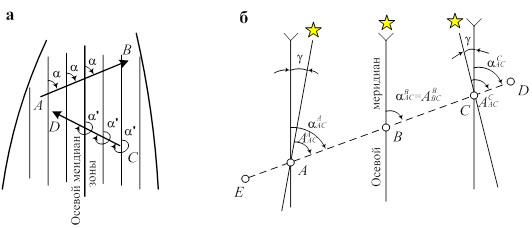
Дирекционные углы (а) и сближение меридианов (б)

Рис. 2.3

Дирекционным углом называют угол a, отсчитываемый по ходу часовой стрелки от северного направления линии, параллельной оси абсцисс, до данной линии. Дирекционные углы могут иметь значения от 0 до 360°.

Дирекционные углы, определенные в одном направлении линии называют прямыми a_АВ, a_CD, в противоположном – обратными a_ВА, a_DC. В отличие от азимута А дирекционный угол a одной и той же линии в разных ее точках остается постоянным. Поэтому прямой и обратный дирекционные углы отличаются друг от друга на 180°.

Проведем прямую ED (рис. 2.3,а) в пределах одной зоны, но пересекающую осевой меридиан, проходящий через точку В. Пусть через точки А и С проведены географические меридианы и линии, параллельные осевому меридиану. В этом случае дирекционный угол a линии ED в точках А, В, С будет иметь одно и тоже значение. Географические азимуты линии ED, взятые в точках А, В и С, не равны между собой, причем в точке В, находящейся на осевом меридиане, азимут линии и дирекционный угол равны. В точках А и С дирекционные углы a отличаются от азимутов на углы g. Угол g, представляющий собой разность между географическим азимутом линии в какой-либо точке и дирекционным углом этой линии, называется сближением меридианов, т.е. .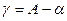

Для точек местности, расположенных к востоку от осевого меридиана, сближение меридианов положительное, а для точек, расположенных к западу от него – отрицательное. Таким образом, если определен азимут (например, из астрономических наблюдений) какой-либо линии, а также известно сближение меридианов, то можно вычислить дирекционный угол этой линии по формуле:

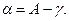
Раздел III. ТОПОГРАФИЧЕСКИЕ КАРТЫ И ПЛАНЫ

Масштабы

Построение карт, планов, профилей, разрезов производится с уменьшением изображаемых объектов. Степень уменьшения линии на плане определяется масштабом, выражаемым ответвленным числом, в котором числитель – единица, знаменатель – число, показывающее, во сколько раз горизонтальное проложение линии местности уменьшено по сравнению с его изображением на плане. Такой масштаб называется численным и выражается дробью 1/М, где М – знаменатель численного масштаба.

На планах и картах значения численного масштаба подписываются следующим образом: 1:500, 1:1000, 1:2000, 1:10000, 1:25000 и т.д. Приведенные выше значения численных масштабов показывают, что горизонтальные проложения линий местности на картах (планах) уменьшены соответственно в 500, 1000, 2000, 10000 и 25000 раз.

Например, если горизонтальное проложение линии местности равно 174,3 м, масштаб плана 1:2000, то длина линии на плане – 174,3:20=8,71 см, или, если линия на плане масштаба 1:5000 равна 10,20см, то горизонтальное проложение этой линии местности будет 10,20*50=510,0 м.

На картах и планах численный масштаб записывается также именованными масштабами, где за единицу измерения на карте (плане) принимают 1 см, а горизонтальное проложение, ему соответствующее на местности, выражается в метрах или километрах. Например, для численного масштаба 1:10000 именованный записывается следующим образом: «в сантиметре 100 метров».

Различают масштабы крупные и мелкие. Чем меньше знаменатель численного масштаба, тем масштаб считается крупнее. Наиболее крупными масштабами карт и планов будут соответственно масштабы 1:500 – 1:10000, а наиболее мелкими – 1:50000 – 1:1000000. На плане и карте более крупного масштаба можно отобразить больше подробностей местности. Масштаб карты и плана выбирается согласно техническим инструкциям в зависимости от их назначения.

На практике для перевода длины линий местности в ее длину на плане или для решения обратной задачи используют графические построения в виде линейного и поперечного масштабов.

На рис. 3.1,а показаны линейные масштабы, представляющие собой шкалы, разделенные на равные отрезки, называемые основанием масштаба; отрезки принимаются равными 1, 2 или 2,5 см, что должно соответствовать круглому числу метров на местности (5, 10, 20, 50, 100, 200 м и т.д.). Первые слева основания делятся на равные части. Подпись 0 ставится справа первого основания. Остальные штрихи, обозначающие концы оснований, надписываются в соответствии с принятым численным масштабом плана. Изображенные линейные масштабы построены по численным масштабам 1:50000 и 1:100000. Основание линейного масштаба в первом случае равно 2 см, во втором – 1 см. Наименьшие деления левых оснований при подписанном значении 1000 м (1 км) соответственно равны 500 м и 100 м.

При пользовании линейным масштабом измеряемое на плане расстояние берут в раствор измерителя, затем одну из игл устанавливают на штрих одного из оснований таким образом, чтобы вторая игла располагалась внутри крайнего левого основания. Десятые доли наименьшего деления оценивают на глаз.

Для того, чтобы избежать оценки делений на глаз и таким образом повысить точность измерения и построения отрезков на картах и планах, применяют номограмму, построенную на основаниях линейного масштаба и использующую метод пропорционального клина. Такая номограмма называется графическим масштабом длин или поперечным масштабом (рис. 3.1,б).

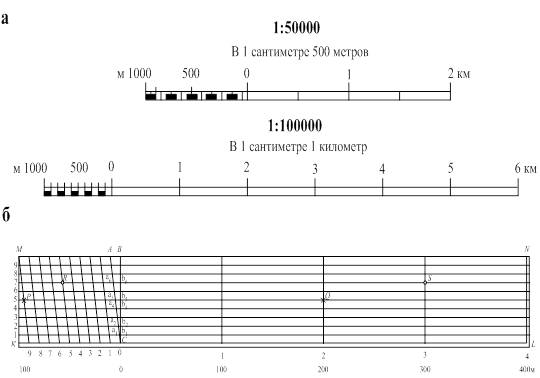Изображение численного, именованного и линейного масштабов на картах (а) и поперечный масштаб (б)

Рис. 3.1

На рис. 3.1,б показан нормальный поперечный масштаб с основанием 2 см. Если принять численный масштаб 1:5000, то для удобства пользования поперечным масштабом его необходимо подписать. В данном случае вдоль линии оснований и вправо и влево от нуля – 100, 200, 300 и 400 м. Для определения по этому масштабу длины линий берут в раствор измерителя соответствующее расстояние на плане, затем одну из игл измерителя ставят на таком перпендикуляре, чтобы вторая игла размещалась на наклонной линии первого основания, при этом обе иглы измерителя должны лежать на одной горизонтальной линии.

Масштаб плана выбирают в соответствии с размерами объекта в натуре и руководствуются точностью масштаба таким образом, чтобы размеры объекта были на плане в 5-10 раз больше 0,1 мм (разрешающая способность человеческого глаза 0,1 мм). Например, если отдельные детали строительных объектов на площадке горного предприятия имеют размеры порядка 1 м, то для их отображения на плане возможен масштаб 1:2000 – 1:1000.

3.2. Разграфка и номенклатура топографических карт и планов

Под картой понимается построенное в картографической проекции, уменьшенное, обобщенное изображение на плоскости поверхности Земли или отдельного ее участка, показывающее расположенные на них объекты в определенной системе условных знаков.

Под топографическим планом понимают изображение на плоскости в ортогональной проекции в крупном масштабе ограниченного участка местности, в пределах которого кривизна уровенной поверхности не учитывается.

Разграфкой называется деление листов одного масштаба на листы более крупного масштаба, номенклатурой – система обозначений отдельных листов карт (трапеций). Границами (рамками) топографических карт являются географические меридианы и параллели. Листы карт разных масштабов имеют следующие размеры, представленные в табл. 3.1.

Таблица 3.1

Номенклатурой называют систему обозначения (нумерации) отдельных листов топографических карт. В основу номенклатуры топографических карт различных масштабов положены листы карты масштаба 1:1000000, являющейся международной картой. Для получения листов этой карты вся земная поверхность делится параллелями на пояса (ряды) через четыре градуса и меридианами – на колонны через шесть градусов. В пересечении поясов и колонн образуется трапеции в 4° по широте и 6° по долготе, каждая из которых изображается на отдельном листе бумаги. Пояса обозначаются заглавными буквами латинского алфавита, начиная от экватора к северу и югу, а колонны нумеруются арабскими цифрами от 1 до 60, начиная от меридиана с долготой 180° в направлении с запада на восток. Номенклатура листа карты масштаба 1:1000000 слагается из букв пояса и числа – номера колонны.

Колонны совпадают с шестиградусными зонами. Но так как колонны начинают считать от меридиана с долготой 180°, их номера отличаются от номера зон на 30.

Переход к листам карты более крупных масштабов осуществляется делением листа карты масштаба 1:1000000.

Лист карты масштаба 1:500000 получается делением каждого масштаба 1:1000000 на 4 части с обозначением каждой части заглавными буквами русского алфавита А, Б, В, Г, которые добавляются к номенклатуре листа карты масштаба 1:1000000 (например, буквы Г, рис. 3.2).

Лист карты масштаба 1:200000 получается путем деления миллионного листа на 36 частей, которые обозначаются римскими цифрами I, II,…, XXXVI, добавляемыми к соответствующей номенклатуре исходного листа карты 1:1000000 (см. рис. 3.2).

Лист карты масштаба 1:100000 получается путем деления миллионного листа на 144 части, которые обозначаются арабскими цифрами, добавляемыми к номенклатуре масштаба 1:1000000 (рис. 3.2).

Лист карты масштаба 1:50000 получается путем деления листа карты масштаба 1:100000 на четыре части, обозначаемых одной из заглавных букв русского алфавита А, Б, В, Г, например N-37-49-А.

Лист карты масштаба 1:25000 получается путем деления листа карты масштаба 1:50000 на четыре части, каждая из которых обозначается одной из строчных букв а, б, в, г, которые ставятся после номенклатуры масштаба 1:50000, например, N-37-49-А-б.