Основы геодезических вычислений

Важной частью геодезических работ являются вычисления, во-первых, потому что на их основе производится анализ всей графики и необходимых оценок для решения инженерных задач, во-вторых, вычисления занимают большой удельный вес во всем комплексе рассматриваемых работ. Для проведения вычислительных работ должен быть установлен порядок математических действий, а также необходимая вычислительная техника. По-прежнему применяются математические таблицы и номограммы.

При геодезических вычислениях приходится иметь дело с так называемыми приближенными числами. Приближенные числа появляются в результате ошибок измерений; из-за неточности формул, методов и моделей; из-за ошибок округлений и т.п. Существуют правила вычислений с приближенными числами, которые позволяют облегчить вычисления и применить наиболее подходящие средства вычислений.

При проведении вычислений необходимо руководствоваться следующими правилами:

• в числах, с которыми оперируют при вычислениях, необходимо различать десятичные знаки, значащие и верные цифры. Десятичными знаками являются все знаки после запятой. Значащими цифрами называются все цифры, кроме нулей слева и тех нулей справа, которые являются результатом округления. Например, у числа 1200, отражающего округленное значение 1211, только две цифры (1 и 2) являются значащими. Верными цифрами называют цифры, заслуживающие доверия в данном числе. Например, в сумме углов треугольника 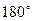все три цифры верные. В числе же 20,372 м, обозначающем длину некоторого отрезка, измеренного с точностью до 1 см, верными цифрами являются 20,37 м;
• точность результата определяется его погрешностью;
• точность вычислений должна соответствовать точности исходных данных, которая определяется практической потребностью;
• при вычислениях числа надо ограничивать всегда таким образом, чтобы все цифры, кроме последней, были верны и лишь последняя была бы сомнительной;
• при сложении и вычитании приближенных чисел, содержащих неодинаковое количество десятичных знаков, целесообразно оставить у них десятичных знаков больше, чем у числа с их наименьшим количеством;
• при умножении двух чисел с одинаковым количеством значащих цифр результат должен иметь столько значащих цифр, сколько их было в сомножителе;
• при умножении или делении приближенных чисел с неодинаковым количеством значащих цифр фактически умножается (делится) столько значащих цифр в каждом числе, сколько их имеется в числе с наименьшим количеством плюс одна цифра. Таким образом, при умножении 21378,28 на 3,25 первое число следует округлить до 21380, а затем произвести действие, при этом в результате следует сохранить столько значащих цифр, сколько их имеет меньший сомножитель. Таким образом, произведение (частное) имеет столько верных значащих цифр, сколько их имеет число с наименьшим количеством значащих цифр;
• при извлечении квадратного или кубического корня из приближенного числа количество значащих цифр в результате должно соответствовать количеству цифр подкоренного выражения. При возведении числа в степень в полученном результате оставляют столько значащих цифр, сколько их в возводимом в степень числе;
• при вычислении среднего какой-либо величины, отдельные значения которой близки, необходимо записать общую часть значения, для остатков вычислить поправки;
• для каждого вычисления следует предварительно составить формуляр.

Для исключения погрешностей вычислений при заполнении вычислительной документации должны соблюдаться некоторые положения, исключающие появление погрешностей вычислений и повышающие эффективность вычислительных работ. Для этого записи в журналах и ведомостях вычислений должны вестись четким почерком хорошо отточенным карандашом, чернилами или тушью. Подскабливание и подтирание вычислений не разрешаются. Места, где найдены погрешности, должны быть перечеркнуты и сделаны записи, указывающее место, где сделаны новые записи. Если вычисления ведутся по схемам, не предусматривающим внутреннего контроля, то они должны быть сделаны независимо двумя исполнителями. Вычисления должны заканчиваться определением погрешностей и обязательным их сравнением с допустимыми величинами, предусматриваемыми соответствующими инструкциями.

Одним из примеров вычислений являются правила округления, заключающиеся в следующем:

1) последнюю цифру необходимо увеличить на единицу, если следующая за ней цифра больше 5, например, 10,276 » 10,28;

2) последняя цифра не изменяется, если следующая за ней меньше 5, например, 121,2873»121,287;

3) последнюю четную цифру необходимо оставить без изменения, если следующая за ней цифра равна 5, например, 27,3745 » 27,374;

4) последнюю нечетную цифру необходимо увеличить на единицу, если следующая за ней цифра равна 5, например, 17,2575 » 17,258.