Одномерные колебания однородной струны
Рассмотрим распространение продольных волн в однородной неограниченной струне с линейной плотностью r. В этом случае движение каждого из элементов струны происходит лишь в направлении ее длины. При распространении продольной волны на элемент толщиной Dx (см. рисунок 7.1) действуют силы: слева Ss(x) и справа Ss(x+Dx), где S - площадь поперечного сечения струны, s(x) и s(x+Dx) - нормальные упругие напряжения.
 |
На элемент Dx действует результирующая сила
F= Ss(x+Dx) - Ss(x).
Под действием этой силы элемент Dx испытывает смещение.
Обозначив u(x,t) смещение центра масс элемента Dx, запишем в соответствии со вторым законом Ньютона уравнение его движения
rSDx 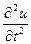 = Ss(x+Dx) - Ss(x),
= Ss(x+Dx) - Ss(x),
здесь rSDx=m - масса элемента Dx, а 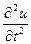 - ускорение. Уравнение можно переписать в виде
- ускорение. Уравнение можно переписать в виде
r 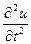 =
= 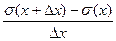 .
.
При Dx®0 оно перейдет в уравнение
r 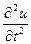 =
= 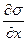 .
.
Согласно закону Гука для изотропных твердых тел
s=Еe,
где Е - модуль упругости (модуль Юнга), 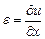 - деформация в точке.
- деформация в точке.
Отсюда
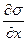 = Е
= Е 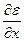 = Е
= Е 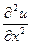 .
.
Тогда уравнение движения для смещения u(x,t) окончательно примет вид
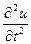 =
= 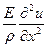 .
.
Это обычное волновое уравнение для упругих волн, распространяющихся вдоль струны. Решение этого уравнения будем искать в виде бегущей монохроматической волны:
u=u0exp[i(kx-wt)]= u0 sin 2p (x/l-νt)= u0sin(kx-wt)
где u0 - амплитуда колебания, ν - частота колебаний, w = 2pν - круговая частота, t - время, l - длина волны, k = 2p/l - волновое число.
После подстановки последнего выражения в волновое уравнение получим дисперсионное соотношение
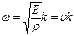 .
.
Из дисперсионного соотношения следует, что для упругой волны, распространяющейся в неограниченно протяженной струне, частота колебаний линейно зависит от волнового числа (см. рисунок 7.2).
 |
При этом скорость распространения волны для данного материала - величина постоянная. Для железной струны (E=2,1×1011 Па, r=7,8×103 кг/м3) имеем 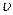 =5×103 м/с.
=5×103 м/с.
Как видно из рисунка 7.2, модуль волнового числа может меняться от 0 до ¥, а следовательно, частота колебаний меняется непрерывно от 0 до ¥. Поскольку энергия Е=2πhω, то энергия колебаний может неограниченно возрастать. Это противоречит физическим представлениям о строении кристаллической решетки. Следовательно, модель струны является слишком грубой вследствие предположения о непрерывности распределения вещества в объеме кристалла. Поэтому рассмотрим случай дискретного распределения вещества.
Дата добавления: 2021-11-16; просмотров: 411;











