Закон Гука для анизотропных твердых тел

Монокристаллические твердые тела являются телами анизотропными. В общем случае для монокристаллов любые произвольно выбранные направления по свойствам неэквивалентны.

Как уже отмечалось, напряжения и деформации описываются тензорами второго ранга, каждый из которых определяется девятью компонента­ми. Если деформация бесконечно мала и однородна, то каждая компонента тензора деформации линейно связана со всеми компонентами тензора напряжений и, наоборот, каждая компонента тензора напряжения линейно связана со всеми компонентами тензора деформаций. В этом заключается сущность закона Гука для анизотропных твердых тел. Математический закон Гука для монокристаллов запишется в виде

,

либо как

,

где 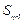и - константы податливости и жесткости кристал­ла соответственно. Всего будет 81 ком­понента и 81 компонента .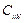

Величины и 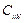образуют тензор четвертого ранга. Тензор, состав­ленный из коэффициентов 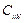, называют тензором упругой жесткости или просто тензором упругости. Тензор, составлен­ный из коэффициентов , называют тензором упругой подат­ливости.

Так как тензоры деформации и напряжения являются сим­метричными тензорами второго ранга ( и 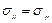), то не­зависимых компонент и 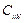будет уже не 81, а только 36, поскольку в этом случае

, ,

, .

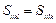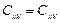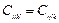Для кристаллов тензоры упругих модулей, каждый из кото­рых составлен из 36 компонент, в свою очередь также являются симметричными, т. е. компоненты и 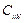симметричны и относительно перестановки пар индексов:

,

.

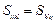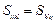Наличие таких равенств приводит к тому, что в общем случае число независимых компонент тензоров упругих модулей сокращается с 36 до 21 - столько констант имеет твердое тело, не обладающее никакой симметрией.

При решении многих конкретных задач для упругих модулей полезна запись в матричных обозначениях, поскольку она уменьшает число индексов у компонентов.

При матричной записи двойное сочетание ij=m и kl=n заменяется одним индексом от 1 до 6 по следующей схеме:

11 - 1; 22 - 2; 33 - 3; 23, 32 - 4; 31, 13 -5; 12, 21 - 6.

Коэффициенты упругой жесткости и упругой податли­вости можно представить в виде таблиц:

,

.

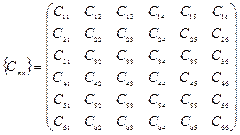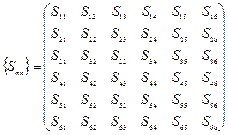Полное число упругих констант сокращается в зависимости от симметрии кристалла. Так, если кристалл обладает триклинной симметрией, то полное число упругих констант равно 21, а для кристаллов кубической симметрии оно равно 3. Основное свой­ство кубического кристалла состоит в том, что направления ±х, ±y, ±z взаимно перпендикулярны и полностью эквивалентны. Это приводит к тому, что для кубических кристаллов имеется лишь три независимые компоненты и набор постоянных упругой жесткости сводится к матрице:

.

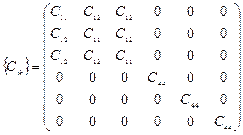Однако, если образец кубического кристалла вырезан в каком-либо направлении, отличающемся даже на малый угол от основных кристаллографических направлений, то он общем случае приобретает свойства кристаллов триклинной системы.

Лекция 7