Механические свойства твердых тел

6.1 Напряжения

6.2 Деформации

6.3 Диаграммы деформаций

6.4 Закон Гука для изотропных твердых тел

6.5 Закон Гука для анизотропных твердых тел

Механические свойства твердого тела отражают его реакцию на воздействие некоторых внешних факторов. В простейшем случае такими внешними факторами являются механические воздействия: сжатие, растяжение, изгиб, удар, кручение. Механические свойства определяются, в первую очередь, силами связи, действующими между атомами или молекулами, составляющими твердое тело.

Напряжения

Если тело находится под действием внешних сил, то в каждой его точке возникают механические напряжения. В этом случае говорят, что тело находится в напряженном состоянии. Если в таком теле выделить какой-либо элемент объема, то на него действуют два типа сил:

1) объемные силы (например, сила тяжести), действующие на все элементы тела; их значение пропорционально объему элемента;

2) силы, действующие на поверхность элемента со стороны окружающих его частей тела. Эти силы пропорциональны площади поверхности элемента. Такую силу, отнесенную к единичной площади, называют напряжением.

Например, при осевом растяжении изотропного цилиндриче­ского стержня (см. рисунок 6.1) в условиях статического равновесия внешняя сила F уравновешивается внутренней силой сопротивления:

.

При описании напряженного состояния будем считать, что напряжение во всем теле однородно, все части тела находятся в равновесии, объемные силы отсутствуют. Выберем любую точку О в объеме этого тела и вокруг нее построим бесконечно малый куб (см. рисунок 6.2).

Три взаимно перпендикулярных оси х, у, z, исходящие из этой точки, выберем в качестве прямоугольной системы координат. Поскольку в дальнейшем при написании формул удобнее оперировать цифрами, обозначим ось х цифрой 1, ось у - цифрой 2 и ось z - цифрой 3. Ребра элементарного куба параллельны осям Ox, Оу, Oz.

При равновесии силы, действующие на противоположные грани, равны, поэтому достаточно рассмотреть силы, действующие на три взаимно перпендикулярные грани. Каждое из напряжений, действующих на три непараллельные грани куба, раскладываем на одну нормальную составляющую и две касательные, т. е. лежащие в рассматриваемой грани.

Обозначим σ_ij компоненту напряжения, действующую в направлении i на грань куба, перпендикулярную оси j. Напряжения σ₁₁, σ₂₂, σ₃₃ - нормальные (растягивающие или сжимающие) напряжения; σ₁₂, σ₁₃, σ₂₃ и т. д. - касательные (скалывающие или сдвиговые) напряжения.

Итак, напряженное состояние в точке характеризуется девятью величинами σ_ij, которые являются компонентами тензора второго ранга - тензора механических напряжений:

.

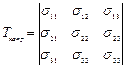Так как элементарный куб находится в состоянии равновесия, то можно показать, что σ₁₂ = σ₂₁, σ₁₃ = σ₃₁, σ₂₃ = σ₃₂. Отсюда следует, что из девяти компонент только шесть являются независимыми и тензор оказывается симметричным, т. е. компоненты, симметричные относительно главной диагонали тензора, равны между собой (σ_ij = σ_ji).

Напряженное состояние, возникающее в твердом теле, существенно влияет на процессы его деформации и разрушения. Важной характеристикой напряженного состояния является коэффициент «мягкости», равный отношению максимальных касательных напряжений к максимальным нормальным. Чем меньше этот коэффициент, тем «жестче» напряженное состояние. Касательные напряжения способствуют развитию пластической деформации, а нормальные - разрыву межатомных связей, хрупкому разрушению твердого тела.

Деформации

Деформация - изменение объема или формы твердого тела без изменения его массы под действием внешней силы. Деформация - это процесс, при котором изменяется рас­стояние между какими-либо точками тела. Простейшие виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб.

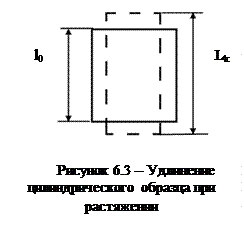
Элементарной деформацией при одноосном растяжении цилиндрического образца является удлинение. При приложении растягивающей силы образец увеличивается в длине и уменьшается в диаметре. Обычно деформацию выражают в относительных единицах. Так, если образец имел начальную длину l₀ и l_k после приложения растягивающей силы (см.рисунок 6.3), то относительная деформация образца

.

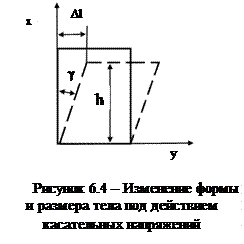
Для полного описания деформированного состояния кроме удлинений (укорочений) необходимо знать сдвиги, возникающие под действием касательных напряжений. При механических испытаниях принято характеризовать деформации относительным изменением линейных размеров образцов, а также углом сдвига, т. е. углом, на который изменился первоначальный прямой угол элемента поверхности деформируемого тела или образца. Относительным сдвигом называют тангенс угла сдвига (см. рисунок 6.4):

.

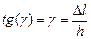Любая деформация может быть представлена в виде определенной комбинации сдвигов и удлинений. В общем случае деформированное состояние в выбранной точке характеризуется девятью величинами ε_ij, которые являются компонентами тензора второго ранга - тензора деформаций:

.

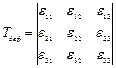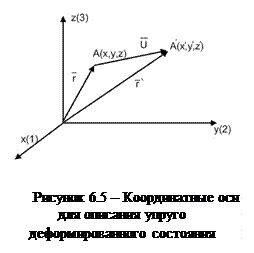Рассматривая случай объемной деформации твердого тела, выберем в качестве осей координат три ортогональные оси х, у, z с началом в точке О (см. рисунок 6.5). Пусть точка О после деформации осталась на месте, а все остальные точки тела изменили свои положения. Определим положение точки А (х, у, z) до деформации радиус-вектором 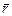. После деформации точка А (х, у, z) переместится в положение А^' (х^', у^', z^'), определяемое радиусом-вектором . Вектор называется вектором смещения, 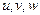- компоненты вектора смещения по осям x, y, z.

Компоненты вектора смещения связаны с компонентами тензора деформаций соотношениями Коши:

, , ,

,

,

.

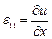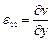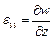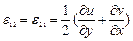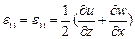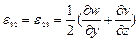Компоненты 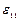, , 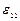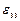задают относительное удлинение вдоль соответствующих осей, а компоненты , , 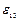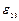задают изменения углов, вызванные приложением нагрузки.