Несимметричные алгоритмы шифрования
В середине 70-х двое ученых — Винфилд Диффи и Мартин Хеллман — описали принципы шифрования с открытыми ключами. Особенность шифрования на основе открытых ключей состоит в том, что одновременно генерируется уникальная пара ключей, таких, что текст, зашифрованный одним ключом, может быть расшифрован только с использованием второго ключа и наоборот.
В модели криптосхемы с открытым ключом также три участника: отправитель, получатель, злоумышленник . Задача отправителя заключается в том, чтобы по открытому каналу связи передать некоторое сообщение в защищенном виде. Получатель генерирует на своей стороне два ключа: открытый Е и закрытый D. Закрытый ключ D (часто называемый также личным ключом) абонент должен сохранять в защищенном месте, а открытый ключ Е он может передать всем, с кем он хочет поддерживать защищенные отношения. Открытый ключ используется для шифрования текста, но расшифровать текст можно только с помощью закрытого ключа. Поэтому открытый ключ передается отправителю в незащищенном виде. Отправитель, используя открытый ключ получателя, шифрует сообщение X и передает его получателю. Получатель расшифровывает сообщение своим закрытым ключом D.
Очевидно, что числа, одно из которых используется для шифрования текста, а другое — для дешифрирования, не могут быть независимыми друг от друга, а значит, есть теоретическая возможность вычисления закрытого ключа по открытому, но это связано с огромным количеством вычислений, которые требуют соответственно огромного времени. Поясним принципиальную связь между закрытым и открытым ключами следующей аналогией.
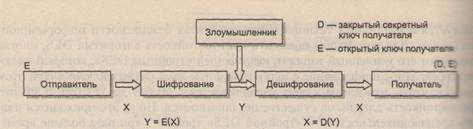
Рис. 1.Модель криптосхемы с открытым ключом
Пусть абонент 1 (рис. 2, а) решает вести секретную переписку со своими сотрудниками на малоизвестном языке, например санскрите. Для этого он обзаводится санскритско-русским словарем, а всем своим абонентам посылает русско- санскритские словари. Каждый из них, пользуясь словарем, пишет сообщения на санскрите и посылает их абоненту 1, который переводит их на русский язык. пользуясь доступным только ему санскритско-русским словарем. Очевидно, что здесь роль открытого ключа Е играет русско-санскритский словарь, а роль закрытого ключа D — санскритско-русский словарь. Могут ли абоненты 2, 3 и 4 прочитать чужие сообщения S2, S3, S4 , который посылает каждый из них абоненту 1? Вообще-то нет, так как, для этого им нужен санскритско-русский словарь, обладателем которого является только абонент 1. Но теоретическая возможность этого имеется, так как затратив массу времени, можно прямым перебором составить санскритско-русский словарь по русско-санскритскому словарю. Такая процедура, требующая больших временных затрат, является отдаленной аналогией восстановления закрытого ключа по открытому.
На рис. 2, б показана другая схема использования открытого и закрытого ключей, целью которой является подтверждение авторства (аутентификации или электронная подпись) посылаемого сообщения. В этом случае поток сообщений имеет обратное направление — от абонента 1, обладателя закрытого ключа к его корреспондентам, обладателям открытого ключа Е. Если абонент 1 хочет аутентифицировать себя (поставить электронную подпись), то он шифрует известный текст своим закрытым ключом В и передает шифровку своим корреспондентам. Если им удается расшифровать текст открытым ключом абонента, это доказывает, что текст был зашифрован его же закрытым ключом, а значит именно он является автором этого сообщения. Заметим, что в этом случае сообщения S2, S3, S4, адресованные разным абонентам, не являются секретными, так как все они — обладатели одного и того же открытого ключа, с помощью которого они могут расшифровывать все сообщения, поступающие от абонента 1.
Если же нужна взаимная аутентификация и двунаправленный секретный обмен сообщениями, то каждая из общающихся сторон генерирует собственную пару ключей и посылает открытый ключ своему корреспонденту.
Для того чтобы в сети все п абонентов имели возможность не только принимать зашифрованные сообщения, но и сами посылать таковые, каждый абонент должен обладать своей собственной парой ключей Е и D. Всего в сети будет 2n ключей: n открытых ключей для шифрования и п секретных ключей для дешифрования. Таким образом решается проблема масштабируемости — квадратичная зависимость количества ключей от числа абонентов в симметричных алгоритмах заменяется линейной зависимостью в несимметричных алгоритмах. Исчезает и задача секретной доставки ключа. Злоумышленнику нет смысла стремиться завладеть открытым ключом, поскольку это не дает возможности расшифровывать текст или вычислить закрытый ключ.
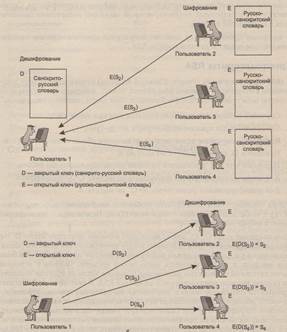
Рис. 2. Две схемы использования открытого и закрытого ключей
В настоящее время одним из наиболее популярных криптоалгоритмов с открытым ключом является криптоалгоритм RSА. В 1978 году трое ученых (Ривест, Шамир и Адлеман) разработали систем кодирования с открытыми ключами RSA , полностью отвечающую всем принципам Диффи-Хеллмана.
Программная реализация криптоалгоритмов типа RSA значительно сложнее и менее производительна, чем реализация классических криптоалгоритмов типа DES. Вследствие сложности реализации алгоритм RSA часто используют только для шифрования небольших объемов информации, например для рассылки классических секретных ключей или в алгоритмах цифровой подписи, а основную часть пересылаемой информации шифруют с помощью симметричных алгоритмов. В табл. 1 приведены некоторые сравнительные характеристики классического криптоалгоритма DES и криптоалгоритма RSA.
Таблица 1. Сравнительные характеристики алгоритмов шифрования
| Характеристика | DES | RSA |
| Скорость шифрования | Высокая | Низкая |
| Используемая функция шифрования | Перестановка и подстановка | Возведение в степень |
| Длина ключа | 56 бит | Более 500 бит |
| Криптоанализ , алгоритм | Перебор по всему ключевому пространству | Разложение числа на простые множители |
| Время генерации ключа | Миллисекунды | Минуты |
| Тип ключа | Симметричный | Асимметричный |
Дата добавления: 2016-06-05; просмотров: 2512;











