AES - передовой стандарт шифрования 21-го века

Современные методы проектирования БСШ. От конкурсов к стандартам

На этой лекции представляются некоторые результаты, связанные с изучением истоков рождения современных наиболее перспективных разработок и решений по построению блочных симметричных шифров, с анализом и изложением идей и принципов, использованных при их построении, позволивших признать эти решения лидерами современных технологий блочного симметричного шифрования. Мы остановимся на двух таких разработках: шифре Rijndael, ставшим победителем конкурсов AES и NESSIE, и шифре IDEA NXT, родившимся на основе шифра IDEA (International Data Encryption Algorithm - Международный алгоритм шифрования данных [20]), разработанного в своё время в качестве предлагаемого стандарта шифрования [21].

Компания MediaCrypt AG - собственник технологии IDEA NXT считает, что IDEA NXT является семейством блочных симметричных алгоритмов шифрования следующего поколения, что и определяет включение этого семейства шифров в круг наших интересов.

AES - передовой стандарт шифрования 21-го века

Шифр Rijndael сегодня считается последним достижением в технологиях проектирования и разработки блочных симметричных шифров. И поэтому, говоря о современных методах проектирования и разработки БСШ, естественно сосредоточить внимание на идеях и принципах, использованных при создании Rijndael-я.

Здесь будут уместно напомнить мысли и соображения, представленные в работе Susan Landau [22, 2004], посвященной изучению алгебраических аспектов разработки Rijndael-я (AES-а).

В этой работе внимание сосредотачивается как раз на проектировании блочных шифров. Автор прослеживает пути, которые привели к шифру Rijndael, считающимся сегодня последним достижением проектных и конструкторских решений. Проводится мысль, что эта разработка стала закономерным итогом развития мировой криптографической мысли.

Так, в [22] отмечается ряд работ и предложений, выполненных на пути к Rijndael-ю. Напомним их здесь.

Willi Meier и Othmar Staffelbach (1989) предположили, что определенные примеры нелинейностей, используемые математиками, могут быть подходящими для криптографического системного проекта [23]. Основываясь на этих идеях, Josef Pieprzyk (1990,1991) предложил алгебраические методы для строительства нелинейных функций [24, 25]. Kaisa Nyberg (1994) исследовала S-блоки и применила, некоторые из идей Pieprzyk-а при проектировании
S-блоков [26]. Joan Daemen (1995) изучил цикловые функции с точки зрения дифференциального и линейного криптоанализа шифра и предложил новую парадигму, подход широкого следа [27]. С другими исследователями, он использовал широкий след и S-блоки Nyberg в криптосистеме SHARK [28, 1996]. Thomas Jakobsen и Lars Knudsen (2001) нашли "интерполяционную атаку" против простых алгебраических шифров, таких как SHARK [29]. Двум разработчикам SHARK-а Daemen и Vincent (1997) Rijmen противопоставили криптосистему Square [30]. Knudsen (1997) взломал Square, используя различные атакующие методы [30]. Rijndael, отмечает автор цитируемой работы, поднялся из праха Square. Далее в работе отслеживается, как эти нити ткали Rijndael.

Значительное внимание уделяется в работе при анализе методов проектирования Rijndael-я новой парадигме, подходу развитому Joan-ом Daemen-ом, получившему название стратегии широкого следа. Следуя [22, 2004] напомним основные идеи этой новой концепции.

Стратегия широкого следа. Автор цитируемой работы отмечает: ²самые различные ниточки формировали основу Rijndael-я². И далее - S-блоки не обеспечивают диффузию; другие шаги цикловой функции должны делать это. Joan Daemen, в то время обучающийся на доктора философии в Katholieke Universiteit в Leuven, предложил новую модель для понимания цикловой функции. Идея Daemen-а, естественная в контексте дифференциального и линейного криптоанализа, состояла в том, чтобы проанализировать цикловую функцию частями (кусками) - S-блоковое преобразование и линейное преобразование - раздельно, чтобы гарантировать, что криптоаналитическая атака не сможет "обойти" нелинейные аспекты алгоритма. Daemen назвал этот подход стратегией широкого следа.

В стратегии широкого следа, цикловое преобразование ρ рассматривается как две отдельных части γ и λ [30, 1997]:

· γ - нелинейное преобразование, которое манипулирует битами локально (где локально обозначает, что выходной бит зависит от небольшого множества входных битов, и выходные биты поблизости зависят от соседних входных битов);

· λ - линейное смешивающее преобразование с высокой диффузией; λ может быть отождествлено с 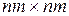матрицей М: λ(a) = b, если и только если М·a = b.

Каждый цикл состоит из трех частей: сначала γ, затем λ, и окончательно ключевое дополнение (сложение с ключом) σ[k^(r)], где k(r) - цикловой подключ для r-того цикла (см. рисунок 1.1). Эти части анализируются отдельно.

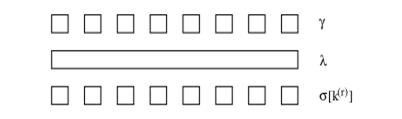
Рис. 1.1. Стратегия широкого следа: слоеобразование

В подходе широкого следа, все S-блоки идентичны. Стратегия широкого следа состоит в том, что:

• Выбирают S-блоки, для которых как максимальная вероятность любого дифференциального следа (дифференциальная вероятность), так и максимальная корреляция линейных комбинаций входных и выходных битов имеют как можно меньшие значения[1].

• Выбирают линейные преобразования таким образом, чтобы не имелось следов с (малым числом) несколькими активными S-блоками.

Последнее - “Широта” стратегии широкого следа. Стратегия проектируется так, чтобы распространить диффузию широко, чтобы развить диффузию соответственно математическим принципам, и чтобы выполнять диффузию по пути, поддающемуся математическому анализу. Это контрастирует с диффузией DES, которая статистически поддается анализу, но оказывается далекой от любой очевидной структуры.

В DES, диффузия происходит на битовом уровне. Daemen и Rijmen предложили отличающуюся модель. Они пренебрегли диффузией, которая происходит в пределах S-блоков, и сосредоточились на диффузии, обеспечиваемой λ частью “линейно смешивающего” преобразования.

Криптоанализ выполнить легче всего, когда в каждом цикле активен единственный (один) S-блок. Поэтому проектировщик криптографического алгоритма должен стремиться избежать худшего случая диффузии, когда встречается единственный активный S-блок. Ясно, лучшее, что может быть сделано проектировщиком с точки зрения достижения верхней границы, это чтобы число ветвлений B[2]⁾ было равно n + 1, где n - число связок (каждая связка состоит из m битов). Обратимое линейное отображение, которое достигает этого эффекта, называется оптимальным. Daemen-у и Rijmen-у удалось построить такое отображение. Они показали, что сепарабельные коды с максимальным минимальным расстоянием обеспечивают путь строительства таких оптимальных линейных преобразований. Это отображение оказалось существенно эффективнее многих других используемых в шифрах линейных преобразований.

Цели проекта Rijndael. Заслуживают внимания также цели проекта Rijndael в интерпретации Susan Landau. Для проектировщиков Rijndael-я безопасность была предварительным выбором, эффективность была вторым беспокойством, отмечает она. Daemen и Rijmen искали простоту - простоту спецификации и простоту анализа [31, p. 65]. Не каждый криптограф видит простоту, как важную цель. Два финалиста AES-а, MARS и Twofish имеют намного более сложные проекты (некоторые наблюдатели посчитали, что эта сложность стала частью причин, по которым эти два алгоритма не были выбраны как Продвинутый Стандарт Шифрования, поскольку их цикловые функции были просто трудными, чтобы их проанализировать полностью). Стратегия широкого следа - простая парадигма, чтобы защититься от атак дифференциального и линейного криптоанализа. Во всех вариантах алгоритмов, которые применяли эту стратегию - SHARK, Square и Rijndael - Daemen и Rijmen использовали простые примитивы. Таким образом, шаг Square для доказательства достаточности оказался не совсем хорошим, траспозиция, была естественным и простым путем осуществить смешивание колонок. В Rijndael-е, следующем экземпляре широкого следа, этот шаг был заменен перестановкой строк, только немного более сложной функцией, которая появляется, чтобы достигнуть цели.

Простота порождает другие критерии, в том числе симметрию. Rijndael показывает симметрию между циклами, и в пределах их.

Daemen и Rijmen, пишет Susan Landau, имели незаявленную цель в разработке своего алгоритма: прозрачность. Они не захотели, чтобы имелись подозрения о наличии в шифре лазеек. Многочлен, определяющий поле - первый вход в таблицу неприводимых полиномов Lidl-а и Niederreiter-а 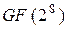[32]. В использованном открытом списке выбора параметров проектировщики Rijndael-я показали, что у них нет ничего в запасе. Простота

x⁸ + 1 и x⁴ + 1 - другая демонстрация отсутствия скрытых параметров.

Daemen и Rijmen предпочли, чтобы перемешивание столбцов (колонок), было обратимым и линейным в 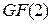, и чтобы диффузия была хорошей. В то же время, чтобы оно было быстрым на 8-разрядных процессорах. Многочленное умножение удовлетворяет обратимости, линейности в 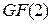, и простоте для описания - это было естественным выбором. Простые мультипликативные коэффициенты 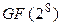быстрее всего на 8-разрядных процессорах. Соответственно умножение на полином 3x³ + x² + x + 2 работает хорошо, отмечает Susan Landau. Многочлены x⁷ + x⁶ + x² + x, x⁷ + x⁶ + x⁵ + x⁴ + 1 и 3x³ + x² + x + 2 не имеют элегантного объяснения для выбора полиномов x⁸ + 1 и x⁴ + 1. Тем не менее, аргументы - самый "простой среди всех многочленов, взаимно простых с модулем" и "линейный в 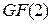), сильно разреженный, быстро реализуемый на 8-разрядных процессорах" - делают ясным, что ничего скрытого здесь также нет.

Проектировщики Rijndael-я достигли эффективности. Алгоритм был значительно быстрее, чем все другие финалисты в ключевых настройках, и был посредине пакета для шифрований.

Расшифрование для Rijndael-я оказалось более медленным, потому что ключевая настройка берет больше времени, но замедление не чрезмерное. Анализ Агенства национальной безопасности аппаратных выполнений показал, что Rijndael является разумным и по его макетному размеру и по имеющейся превосходной "производительности" (объему работы, проделанной в течение определенного периода) [33].

В общем Daemen-у и Rijmen-у удалось создать конструкцию, которая сумела завоевать доверие и поддержку большинства экспертов и специалистов мирового уровня.