Уравнение движения электропривода

Выше были рассмотрены условия работы электропривода в установившемся режиме, когда момент, развиваемый двигателем, равен моменту сопротивления механизма и скорость привода является постоянной. Однако во многих случаях привод ускоряется или замедляется, и тогда возникает инерционная сила или инерционный момент, которые двигатель должен преодолевать, находясь в переходном режиме. Таким образом, переходным режимом электропривода называют режим работы при переходе от одного установившегося состояния к другому, когда изменяются скорость, момент и ток.

Причинами возникновения переходных режимов в электроприводах является либо изменение нагрузки, связанное с производственным процессом, либо воздействие на электропривод при управлении им, т. е. пуск, торможение, изменение направления вращения и т. п. Переходные режимы в электроприводах могут возникнуть также в результате аварий или нарушения нормальных условий электроснабжения (например, изменения напряжения или частоты сети, несимметрия напряжения и т. п.).

Уравнение движения электропривода должно учитывать все силы и моменты, действующие в переходных режимах.

При поступательном движении движущая сила 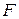всегда уравновешивается силой сопротивления машины 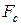и инерционной силой 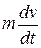, возникающей при изменениях скорости. Если масса тела 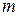выражена в килограммах, а скорость 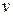– в метрах в секунду, то сила инерции, как и другие силы, действующие в рабочей машине, измеряются в ньютонах (кг·м·с ^-2).

В соответствии с изложенным уравнение равновесия сил при поступательном движении записывается так:

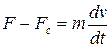. (2.14)

Аналогично уравнение равновесия моментов, Н·м, для вращательного движения (уравнение движения привода) имеет следующий вид:

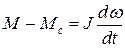. (2.15)

Уравнение (2.15) показывает, что развиваемый двигателем вращающий момент 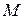уравновешивается моментом сопротивления 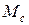на его валу и инерционным или динамическим моментом 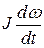. В (2.14) и (2.15) принято, что масса тела 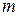и соответственно момент инерции привода 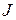являются постоянными, что справедливо для значительного числа производственных механизмов. Из анализа (2.15) видно:

1) при 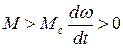, т. е. имеет место ускорение привода;

2) при 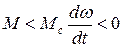, т.е. имеет место замедление привода (очевидно, что замедление привода может быть и при отрицательном значении момента двигателя);

3) при 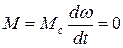, в данном случае привод работает в установившемся режиме.

Вращающий момент, развиваемый двигателем при работе, принимается положительным, если он направлен в сторону движения привода. Если он направлен в сторону обратную движению, то он считается отрицательным. Знак минус перед 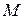, указывает на тормозящее действие момента сопротивления, что отвечает усилию резания, потерям трения, подъему груза, сжатию пружины и т. п. при положительном знаке скорости.

При спуске груза, раскручивании или разжатии пружины и т. п. перед 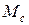ставится знак плюс, поскольку в этих случаях момент сопротивления помогает вращению привода.

Инерционный (динамический) момент (правая часть уравнения моментов) проявляется только во время переходных режимов, когда изменяется скорость привода. При ускорении привода этот момент направлен против движения, а при торможении он поддерживает движение. Инерционный момент как по значению, так и по знаку определяется алгебраической суммой моментов двигателя и момента сопротивления.

При учете сказанного о знаках моментов формула (2.15) соответствует работе двигателя в двигательном режиме при реактивном моменте сопротивления (или при потенциальном тормозящем моменте сопротивления). В общем виде уравнение движения привода может быть записано следующим образом:

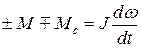. (2.16)

Выбор знаков перед значениями моментов в (2.16) зависит от режима работы двигателя и характера моментов сопротивления.