Ранжирование и оценка

При решении многих практических задач ча­сто оказывается, что факторы, определяющие конечные результаты, не поддаются непосредственному измерению. Расположение этих факторов в порядке возрастания (или убывания) какого-либо присущего им свойства назы­вается ранжированием. Ранжирование позволяет выбрать из исследуемой совокупности факторов наиболее существенный.

Бывает, что явления имеют различную природу и вследствие этого несоизмеримы, т. е. у них нет общего эталона сравнения. И в этих случаях установление относительной значимости с помощью экспертов облегчает выбор наиболее предпочтительного.

Ранжирование может применяться в следующих ситу­ациях:

1) когда необходимо упорядочить какие-либо явления (объекты) во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженно­сти какого-либо их качества, а лишь взаимным прост­ранственным или временным расположением этих явле­ний (объектов).

2) когда нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется про­изводить его точное измерение.

3) когда какое-либо качество в принципе измеримо, однако в настоящий момент не может быть измерено по причинам практического или теоретического характера.

Рассмотрим существо процедуры ранжирования под­робнее. При ранжировании эксперт должен расположить объекты (альтернативы) в порядке, который представ­ляется ему наиболее рациональным, и приписать каждо­му из них числа натурального ряда — ранги. При этом ранг 1 получает наиболее предпочтительная альтернати­ва, а ранг N — наименее предпочтительная.

Следовательно, порядковая шкала, получаемая в ре­зультате ранжирования, должна удовлетворять условию равенства числа рангов N числу ранжируемых объек­тов п.

Бывает так, что эксперт не в состоянии указать поря­док следования для двух или нескольких объектов либо он присваивает разным объектам один и тот же ранг, и в результате число рангов N оказывается не равным числу ранжируемых объектов п. В таких случаях объектам приписывают так называемые стандартизированные ран­ги. С этой целью общее число стандартизированных ран­гов полагают равным n, а объектам, имеющим одинако­вые ранги, присваивают стандартизированный ранг, зна­чение которого представляет среднее суммы мест, поде­ленных между собой объектами с одинаковыми ран­гами.

Когда ранжирование производится несколькими (т) экспертами, обычно сначала для каждого объекта подсчитывают сумму рангов, полученную от всех экспертов, а затем, исходя из этой величины, устанавли­вают результирующий ранг для каждого объекта. Наи­высший (первый) ранг присваивают объекту, получившему наименьшую сумму рангов, и, наоборот, объекту, получившему наибольшую сумму рангов, присваивают самый низкий ранг N. Остальные объекты упорядочива­ют в соответствии со значением суммы рангов относи­тельно объекта, которому присваивается первый ранг.

Точность и надежность процедуры ранжирования в значительной степени зависят от количества объектов. В принципе, чем таких объектов меньше, тем выше их «различимость» с точки зрения эксперта, а следователь­но, тем более надежно можно установить ранг объекта. Во всяком случае количество ранжируемых объектов п не должно быть больше 20, а наиболее надежна эта про­цедура, когда n<10.

Метод ранжирования редко используется «в чистом виде». Чаще всего он сочетается с другими методами, обеспечивающими более четкое различие между факто­рами. Одним из них является метод непосредственной оценки и некоторые его модификации.

3.3. Метод непосред ственной оценки

Метод непосредственной оценки состоит в том, что диапазон изменения какой-либо качественной переменной разбивается на несколько интервалов, каж­дому из которых присваивается определенная оценка (балл), например от 0 до 10. Шкала оценок может быть не только положительной, а, например, включать в себя диапазон с интервалом оценок от —3 до +3. Задача эксперта заключается в помещении каждого из рассмат­риваемых объектов (факторов) в определенный оценоч­ный интервал, либо в соответствии со степенью облада­ния тем или иным свойством; либо в соответствии с пред­положениями эксперта об их значимости. Заметим, что число интервалов, на которые разбивается весь диапазон изменения качества, не обязательно должно быть одина­ково для каждого эксперта. Кроме того, каждому эк­сперту разрешается давать одну и ту же оценку двум (или нескольким) качественно различным факторам.

В некоторых случаях оказывается удобнее для выбо­ра наиболее предпочтительного фактора сначала произ­вести оценку, а затем — ранжирование.

В ряде случаев суммарные оценки рангов нормируют­ся. Нормирование любой меры означает, что представ­ляющее ее число для всего множества в целом прини­мается равным единице. Нормирование позволяет устано­вить более тесную связь между оценками, приписанными экспертами отдельным объектам. С этой целью оценки по всем объектам суммируются, а затем каждая из них де­лится на полученную сумму. Рассчитанные таким образом нормированные оценки могут быть вновь проранжированы.

Когда в экспертизе участвует несколько экспертов, обычно стремятся получить усредненную оценку (вес) для каждого объекта. Для этого нормированные оценки каждого объекта суммируются, а затем полученная сум­ма делится на число экспертов.

При наличии нескольких факторов, по которым следует оценить каждый из объектов, средняя оценка (вес) каждого объекта может быть рассчитана по формуле

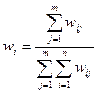, (2)

где w_ij – вес i-го объекта, подсчитанный по оценкам всех экспертов.

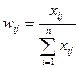, (3)

где x_ij – оценка фактора i, данная экспертом j;

n – число факторов;

m – число экспертов.

Другой способ установления зависимости между оценками факторов (объектов, характеристик) состоит в том, что важнейшему (с точки зрения экспертов) фак­тору назначается оценка (вес), равная наперед заданно­му числу (обычно 1 или 10), а оценка следующих друг за другом по важности факторов определяется последо­вательно как доля более важного. Полученные таким об­разом значения нормируются. Основное достоинство та­кого способа заключается в том, что он облегчает про­цесс выбора оценок, поскольку эксперту не нужно каж­дый раз сопоставлять весь их ряд, а лишь учитывать зна­чение первой и предыдущей по важности оценок. Оценки, полученные от группы экспертов, могут быть усреднены для каждого фактора путем расчета средней арифмети­ческой.

В случаях, когда группа, состоящая из нескольких экспертов, оценивает ряд факторов, причем у каждого из экспертов имеется своя шкала предпочтений, для нахож­дения усредненной оценки каждого фактора может быть рекомендована следующая методика:

1) составляется матрица «эксперты — факторы», в ко­торой проставляются полученные от каждого эксперта оценки факторов по шкале от 0 до 10.

2) рассчитывается относительная значимость (W_ij) всех факторов в отдельности для каждого эксперта. С этой целью оценки, полученные от каждого эксперта, суммируются (по горизонтали), а затем нормируются.

3) вычисляется усредненная оценка, данная всеми экспертами каждому фактору. Для этого нормированные оценки, полученные в предыдущем шаге, суммируются (по вертикали), а затем рассчитывается средняя ариф­метическая для каждого фактора.

В случае большого числа факторов могут возникнуть трудности при оценке экспертами большого числа факторов. В этом случае рекомендуется применять двухэтапный метод ранжирования.

На первом этапе осуществляется ранжирование предварительно сформированных групп факторов.

На втором этапе факторы ранжируются внутри отдельных групп.

Задачей следующего этапа является получение на основе синтеза группового и внутригруппового ранжирования единой системы расположения всех факторов. Для решения этой задачи могут быть применены несколько способов.

1. Простое ранжирование. Оно заключается в том, что все факторы располагаются в последовательности, соответствующей значимости отдельных групп и значимости факторов внутри групп.

Преимуществом этого способа является простота и лёгкость получения единой классификации факторов. Но установленная подобным образом общая ранжировка очень огрубленная. При таком способе ранжировки совершенно игнорируется возможность ситуации, когда факторы, стоящие на первых местах в следующей по значению группе, могут быть более важны, нежели стоящие на последних местах в предыдущей группе.

2. Ранжирование по сумме оценок. В основе ранжирования по этому способу лежит величина, получаемая при сложении оценок места группы и места фактора внутри группы. В качестве оценки в обоих случаях ис­пользовалось значение средневзвешенного места. Ранжирование по сумме оценок бо­лее объективно, поскольку учитывает степень различия в оценках мест групп и факторов внутри групп. Однако при этом способе возможно и механическое суммирова­ние в связи с тем, что оценки мест групп и факторов могут быть даны в разных шкалах. Получается, что каждый раз с величиной, измеренной в одном мас­штабе, складываются величины, выраженные в других масштабах. Этот дефект можно устранить, если проводить ранжирование по треть­ему способу.

3. Ранжирование по сравнимой шкале. Чтобы выра­зить ценность места внутри группы в той же системе измерения, которая принята для групп, исполь­зуется следующий прием. Оценки факторов внутри каж­дой группы суммируются, и на эту сумму делится оценка группы. Полученная при этом величина представ­ляет вес единицы внутригрупповой шкалы, выраженный в единицах другой шкалы. Умножая на этот коэф­фициент место каждого фактора, получаем скорректиро­ванные средневзвешенные значения, по которым произ­водится ранжирование.

Недостатком третьего способа является то, что величина корректировочного коэффициента в сильной мере зависит от числа факторов, вошедших в группy. Для его устранения было предложено комбинирование второго и третьего способов (способ 4).

4. Ранжирование комбинированным способом. За оценку места фактора принималась сумма: оценка группы плюс, скорректированная оценка фактора в группе.

Дальнейшее ранжирование состоит в упорядочении их расположения по величине полученной оценки.

Метод непосредственной оценки может быть использован в самых различных ситуациях, характеризующихся отсутствием полной информации, например для оценки трудоемкости научно-исследовательских работ, когда нет сходных отчетно-статистических данных. В таких случаях оценка трудоемкости может производиться специалистами лишь примерно, на основе имеющейся у них информации. Эта информация имеет некоторую долю неоп­ределенности, величина которой зависит от опыта и зна­ний специалистов-экспертов.

3.4. Метод последовательных сравнений

Общим дефектом показателей, получаемых на основе суммирования оценок, является то, что недостаток качества по одному из факторов можно компенсировать за счёт другого, получая один и тот же результат при раз­ной значимости факторов. Поэтому для повышения надёжности подобных оценок весьма важное значение имеет выявление связей и установление зависимостей (по возможности количественных) между всеми значимыми факторами.

Как было показано ранее, аддитивность оценок присуща шкале отношений и при некоторых условиях — шкале интервалов. Поэтому суммирование баллов, расчет результирующих рангов и оценок должны быть основаны не только на их упорядочении, но и еще на некоторых логических допущениях о зависимостях, используя которые можно обоснованно приписывать качественно различным факторам веса в одинаковых единицах по общей шкале измерения.

Основные из этих допущений заключаются в следующем:

1) каждому результату (событию, фактору) соответствует действительное неотрицательное число v_j, рассмат­риваемое как оценка истинной значимости (ценности)Q_j;

2) если результат Q_j, более важен, чем Q_k, то v_j>v_k,.И если Q_j равноценен Qk, то v_j=v_k;

3) если оценки v_j и v_k соответствуют результатам Qj и Qk, то оценка v_j + v_k соответствует общему результату Q_j и Q_k.

Последнее допущение и является допущением об ад­аптивности оценок. Это допущение выполняется, когда результаты дискретны, непротиворечивы и взаимно не­зависимы.

Следствиями допущения об аддитивности являются:

1) если результат Q_j, предпочтительнее Q_k, a Q_k предпочтительнее Q_i;, то совместный результат Q_j, и Q_k предпочтительнее Q_i;

2) значимость общего результата Q_j, и Q_k эквива­лентна значимости общего результата, Q_k и Q_j;

3) если общий результат Q_j, и Q_k эквивалентен Q_k, то v_j=0. Отсюда, если существует результат Q_j, удовлетворяющий данному условию, то существует и нулевая точка определенной шкалы, инвариантная к любым преобразованиям шкалы оценок v.

Процедура последовательных сравнений состоит в сле­дующем. Эксперту предоставляется перечень факторов, которые необходимо оценить по их относительной важно­сти и ранжировать. Наиболее важному фактору при­дается оценка v₁=l, а остальным факторам - оценки у, между 0 и 1 в порядке их относительной важности.

Затем эксперт устанавливает, является ли фактор с оценкой 1 более важным, чем комбинация остальных факторов. Если это так, то он увеличивает оценку v₁, чтобы она была больше, чем сумма всех остальных.

Если нет, то он корректирует оценку v₁ (если необхо­димо) так, чтобы она была меньше суммы всех осталь­ных.

Далее определяется, является ли второй наиболее важный фактор с оценкой v₂ более важным, чем все остальные факторы, получившие более низкие оценки; и повторяется та же процедура, что и для v₁. Процедура последовательных сравнений продолжается вплоть до (п - 1)-го фактора.

Таким образом, используемая здесь процедура состо­ит в систематической проверке оценок на базе их после­довательного сравнения.

сформулируем об­щую процедуру метода оценки весов на основе последо­вательных сравнений так:

1) Упорядочить результаты в соответствии с их важ­ностью с точки зрения эксперта.

2) Приписать вес 1,00 результату Q₁ (т. е. v₁=l,00) и другие веса — всем остальным результатам.

3) Сравнить Q₁ с Q₂+ Q₃+;...+ Q_m:

а) если Q₁, предпочтительнее Q₂+ Q₃+;...+ Q_m, изме­нить (в случае необходимости) - значение v₁ так, чтобы выполнялось неравенство v₁>v₂+v₃+ ... +v_m. При этой корректировке, так же как и при всех остальных, следует стремиться к тому, чтобы веса набора (v₂, v_з и т. д.) оста­лись без изменений. Далее следует перейти к шагу 4;

б) если Q₁ и Q₂+ Q₃+;...+ Q_m равноценны, то изме­нить (в случае необходимости) значение v₁, так, чтобы выполнялось равенство v₁= v₂+v₃+ ... +v_m, и затем пе­рейти к шагу 4;

в) если результат Q₁ менее предпочтителен, чем Q₂+ Q₃+;...+ Q_m, то изменить (в случае необходимости) значение v₁ так, чтобы выполнялось неравенство v₁< v₂+v₃+ ... +v_m. Далее сравнить Q₁ с Q₂+ Q₃+;...+ Q_m-1 и повторить описанную процедуру до тех пор, по­ка Q₁ будет или предпочтительнее, или равноценен всем остальным результатам.

4) Сравнить Q₂ с Q₃+ Q₄+;...+ Q_m и выполнить весь шаг 3.

5) Продолжить шаг 4 до тех пор, пока не будет выпол­нено сравнение Q_m-2 c Q_m-1-+ Q_m.

6) Преобразовать каждое полученное значение v_j в нормированное v'_j.

Описанный метод становится громоздким, когда чис­ло результатов равно или более семи. В этом случае мо­жет быть использована следующая процедура:

1) Упорядочить все множество, учитывая предпочте­ния эксперта (экспертов) и не ставя им в соответствие числовых значений.

2) Выбрать случайным образом любой результат из множества, допустим Q_q.

3) Разбить случайным образом оставшиеся результа­ты на подмножества так, чтобы каждое из них содержало не более 6 результатов.

4) Включить в каждое из подмножеств результат, вы­бранный в шаге 1.

5) Применить процедуру, описанную выше, к каждому подмножеству результатов в отдельности, приписав пред­варительно некоторое число v, результату Q_q (например, 1, 10 или 100). При этом, корректируя значения оценок остальных результатов v_j, значение v_s оставляем без из­менений.

6) Сравнить оценки v_j, с предпочтениями, полученными в шаге 1. Если в итоге получены непротиворечивые результаты, следует пронормировать оценки. Об обнаруженных противоречиях надо сообщить эксперту, который (в случае необходимости) меняет значения оценок.

Основой описанного подхода является введение в каждое подмножество результатов некоторой стандартной меры или базиса сравнения. Надежность полученных оценок можно проверить, образуя новые подмножества и используя другие базисные оценки.

Таким образом, применение метода последовательных сравнений основано на предположении о том, что если задан некоторый интервал действительного переменного, скажем от 0 до 1, то эксперт, основываясь на имеющейся у него информации, может установить предварительные оценки для каждого события, а затем уточнить их на основе сравнения с помощью определенной логической процедуры.

Поскольку множества, содержащие 7 и более элемен­тов (результатов), трудно упорядочить с помощью метода последовательных сравнений (процедура становится гро­моздкой), целесообразно разбивать такие множества на несколько подмножеств, каждое из которых включает, в себя не более 6 результатов.

Квантификация (сведение качественных характери­стик к количественным) предпочтений в сложных и ком­плексных проблемах с помощью метода последователь­ных сравнений при наличии большого числа факторов становится затруднительной. В таких случаях следует попытаться разделить проблему на ряд более простых «подпроблем» и задач, для которых сравнительно про­сто выявить предпочтения, либо, если это оказы­вается невозможным, использовать метод парных сравне­ний.

3.5. Метод парных сравнений

Трудности использования ранжирования, не­посредственной оценки и метода последовательных сравнений при выявлении предпочтений для большого числа факторов можно в определенной степени умень­шить, если предложить экспертам произвести сравне­ние этих факторов попарно, с тем чтобы установить в каждой паре наиболее важ­ный.

В методе парных сравнений объекты сопоставляются попарно экспертом (экспертами), а затем выбирается один из них. Будем говорить, что в этом случае эксперт предпочитает данный объект, хотя выбор не обязательно будет выражать его предпочтение. В общем случае эксперт может установить равенство объектов или за­фиксировать свои предпочтения на некоторой шкале.

Основной элементарный акт — сравнение двух объек­тов А и В одним экспертом — можно распространить на случай, когда несколько экспертов рассматривают более чем два объекта. Производить парное сравнение удобно не только тогда, когда число объектов велико, но и в тех случаях, когда различия между объектами настолько ма­лы, что непосредственное ранжирование или оценка не обеспечивают их разумного упорядочения. Таким обра­зом, метод парных сравнений имеет некоторое преимуще­ство перед другими методами упорядочения в случаях, когда объектов много и (или) они трудно различимы.

Чаще всего при парном сравнении двух объектов ог­раничиваются простой констатацией того, что один из них предпочтительнее другого. В отдельных случаях, когда степень предпочтения можно выявить, используют­ся специальные шкалы, где каждой степени предпочте­ния присваивается определенная оценка. Однако про­стейшая форма парных сравнений, когда устанавливается, что объект А «лучше» в некотором отношении объектa В, наиболее удобна, поскольку она уменьшает область возможной несогласованности между экспертами до минимума. Практика показывает, что даже допущение о возможности равенства объектов создает трудности при сборе и обработке информации, полученной от экспертов. Установлено, например, что одни эксперты объявляют объекты равными более охотно, чем другие.

Рассмотрим случай, когда сравниваются попарно три объекта А, В и С. Пусть суждение каждого эксперта со­стоит из простого предпочтения того или иного объекта, причем .«ничьи» не допускаются. Тогда для каждого из трех сравнений (А с В), (А с С), (В с С) возможны два исхода. Общее число исходов — 8, причем 6 из них типа: A ->B, A -> C, B->C (стрелка означает «предпочти­тельнее, чем»). Результаты сравнения в таком случае удобно представить в виде тройки чисел [2, 1, 0], которые указывают, что один объект (не обязательно A) «выигры­вает» два раза, другой - один раз, а третий — ни разу. Два оставшихся результата

A ->В, В->С, С->А,

А<-В, В<-С, С<-А

могут быть представлены как [1, 1, 1] или же как [1³] и названы циклическими триадами. Ясно, что цикличе­ская триада означает непоследовательность в суждениях части экспертов, причем вероятность возникновения цик­лической триады равна 1/4, когда объекты идентичны.

Причины возникновения циклических триад могут со­стоять в недостаточной компетентности эксперта или же в том, что объекты нельзя сравнивать по одной линей­ной шкале, поскольку имеется несколько признаков, по которым они различаются.

Важным свойством парных сравнений является воз­можность выявления таких противоречий, а, следователь­но, установления некоторых критериев предпочтения.

4. Проверка согласованности экспертных оценок

Групповая оценка может считаться достаточно на­дежной только при условии хорошей согласованности от­ветов опрашиваемых специалистов. Поэтому статистиче­ская обработка информации, полученной от экспертов, должна включать в себя оценку степени согласованности мнений экспертов и выявление причин их неоднород­ности.

Оценки, полученные от экспер­тов, могут рассматриваться как случайная переменная, распределение которой отражает суждения специалистов о вероятности того или иного исхода события (призна­ка). Поэтому для анализа разброса и согласованности оценок, полученных от экспертов, применяются обобщен­ные статистические характеристики — средние и меры разброса.

Существуют два основных метода измерения разбро­са: рассматриваются либо расстояния между двумя упо­рядоченными исходами событий, либо средние расстоя­ния результатов отдельных наблюдений от некоторого центрального значения. Показатели первого типа назы­вают вариационным размахом, а второго — средними от­клонениями.

Для оценки вариационного размаха (амплитуды ко­лебаний) R чаще всего используется следующая пара величин — (Xmin, Хтах). По существу, именно эти величины (или расстояние между ними) имеют в виду, когда говорят о размахе вариации. Чтобы, определить любой другой тип вариационного размаха, необходимо добавить ещё какие-то определения. К примеру, вариационный размах между квартилями равен разности между третьтьим и первым квартилями Q₃—Q₁. В этом случае для сравнительного изучения вариаций может быть вычислен коэффициент интерквартильной вариации:

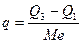, (4)

где q – коэффициент интерквартильной вариации;

Q₃ – граница третьего квартиля;

Q₁ – граница первого квартиля;

Ме – медиана.

Или приблизительно

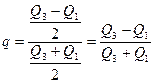, (5)

Коэффициент интерквартильной вариации колеблется между —1 и +1 и приближается к нулю в случае симметричного распределения с очень малой вариацией.

Хорошими характеристиками разброса оценок являются средние отклонения. Среднее абсолютное откло­нение представляет среднюю арифметическую абсолютных величин разностей между каждой оценкой и выборочной средней. В практике статистической обработки оценок, полученных от экспертов, чаще используют не среднее абсолютное отклонение, а среднее квадратическое (стандартное) отклонение и дисперсию.

Среднее квадратическое отклонение есть корень квадратный из среднего квадрата отклонений отдельных значений признака от средней арифметической:

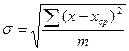, (6)

где σ – среднее квадратическое отклонение;

х — варианты (оценки);

х_ср — средняя арифметиче­ская;

m — число оценок.

Если число оценок не превышает 30, что характерно для большинства -экспертиз, то для расчета среднего квадратического отклонения применяется формула несмещённого среднего квадратического отклонения:

, (7)

Нередко за показатель разброса удобнее принимать не среднее квадратическое отклонение, а его квадрат (σ²). Эта величина называется дисперсией и обладает среди прочих тем свойством, что при увеличении (умень­шении) оценок в k раз, увеличивается (уменьшается) в k²раз.

При анализе согласованности оценок экспертов не­редко используется коэффициент вариации V, характе­ризующий вариабельность, рассчитываемую в виде отно­шения среднего квадратического отклонения к средней арифметической. Обычно он выражается в процентах:

, (8)

Меры рассеяния являются важными характеристика­ми распределения оценок, полученных от экспертов. Од­нако при анализе согласованности оценок недостаточно знать величину вариабельности признака, необходимо также полнее выявить факторы, влияющие на эту измен­чивость по каждому признаку. С этой целью применяют­ся специальные характеристики и показатели.

Нередко при анализе согласованности ответов экспер­тов необходимо оценить связь между альтернативными признаками. Это делается с помощью коэффициентов ас­социации (связи) и коэффициентов контингенции (сопря­женности) .

Связь считается более тесной в том случае, когда каждому значению одного признака соответствуют близ­кие друг другу, тесно расположенные около своей сред­ней величины значения другого признака; связь менее тесная, если эти значения сильно отклоняются от своей средней, т. е. сильно варьируют. Тип, форма и плотность связи обычно выявляются с помощью таких статистиче­ских характеристик, как коэффициент корреляций, кор­реляционное отношение, коэффициент регрессии и неко­торых других.

Большинство статистических методов измерения свя­зей основано либо на принципе взаимной сопряженно­сти, либо на принципе ковариации. О взаимной сопря­женности признаков говорят в случаях, когда интере­суются связью какого-либо выделенного признака с другими признаками при осуществлении, определенного события, причем градация значений признаков по интен­сивности для исследователя безразлична. При обнаружении такой связи предполагается, что существует зависимость между данными признаками.

Основанием для заключения о наличии связи между количественными признаками служит параллельное и одновременное изменение их численных значений. Подобный вывод о наличии связи между признаками основан на принципе ковариации. В математическом отношении задача сводится к вычислению величины ковариации, т. е. сопутствующего изменения численных значений признаков, и последующему нормированию ее с помощью различных приемов.

При оценке связи между признаками используется много самых различных корреляционных показателей, разнообразие которых объясняется стремлением отразить реально существующее разнообразие типов связей в природе и обществе. Поскольку и степень точности расчетов, и вид зависимости между переменными, в конечном счете, выявляются на основе качественного анализа, выбор показателя связи определяется задачами исследования. В некоторых ситуациях в одинаковой степени пригодными для исследования могут оказаться несколько коэффициентов. Решающее значение в этом случае приобретают цели анализа, природа данных (качественные или количественные признаки), требуемая точность расчетов, удобство при вычислении, сравнительная простота интер­претации, а также личный опыт исследователя.

В общем случае статистический анализ согласованно­сти оценок экспертов и получение групповой оценки включает:

1) группировку, агрегирование признаков;

2) оценку степени согласованности ответов экспертов каждому признаку в отдельности и в целом по всему набору;

3) выделение групп экспертов с «близким» мнением относительно порядка признаков в случае наличия существенных расхождений в ответах;

4) выявление причин разброса мнений, определение влияния компетентности и других качеств экспертов на содержание ответов;

5) оценку качества экспертных оценок и компетентности экспертов;

6) формирование группового решения.

Рассмотрим подробнее каждый из этапов анализа.

Необходимость в группировке и агрегировании при­знаков обусловлена рядом обстоятельств. Во-первых, опыт показывает, что отдельные признаки могут быть по-разному истолкованы. Вместе с тем группы признаков, в некотором смысле объективно близкие, истолковывают­ся экспертами более определенно. Следовательно, объ­единяя признаки в группы, можно «извлечь» их однознач­ный смысл и получить более точную и согласованную оценку. Во-вторых, сама оценка значимости (степени влияния) группового фактора более точна и достоверна, чем оценка отдельных признаков. Это объясняется тем, что в групповых оценках устраняются случайные ошибки измерения отдельных признаков при естественном пред­положении, что ошибка оценки одного признака не коррелирует с ошибкой оценки другого. И, наконец, в процес­се ранжирования часто возникают ситуации, когда два или несколько признаков имеют близкие оценки, и эк­сперты не различают их по информативности. В этом случае группировка позволяет определить рациональную степень агрегирования признаков.

Основой решения задачи группировки признаков яв­ляется матрица их взаимосвязи, формализующая понятие близости между признаками, В качестве мер взаимосвя­зи в зависимости от характера идеализации балльных оценок могут выступать коэффициенты корреляции (сильное предположение о метрической шкале), коэффи­циенты взаимной сопряженности (упрощающее предпо­ложение о качественном характере оценок), коэффици­енты ранговой корреляции (предположение о порядковой шкале), коэффициенты близости двух разбиений и др. При проведении исследования полезно использовать раз­ные (две-три) меры связи и оценить степень устойчиво­сти полученных группировок.

Для оценки согласованности ответов по каждому При­знаку данные опроса удобно представить в виде таблицы вариационных рядов ответов (таблица 2).

Таблица 2

Таблица вариационных рядов ответа

Признак	Число мнений о ранге признака	Общее число ответов
		…	i	…	k
x1	f11	f21	…	fi1	…	fk1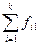
x2	f12	f22	…	fi2	…	fk2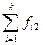
…	…	…	…	…	…	…
xj	f1j	f2j	…	fij	…	fkj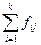
…	…	…	…	…	…	…
xn	f1n	f2n	…	fin	…	fkn

Здесь fij — число ответов о присвоении i-ro места j-му признаку. Если все эксперты дали ответы по всем при­знакам, то итоги строк будут равными.

На основе приведенной таблицы могут быть рассчита­ны меры согласованности ответов экспертов по каждому признаку x_j. Оценка степени согласованности ответов - задача, обратная оценке уровня вариации. Если обозна­чить некоторый показатель вариации j-го признака через μ_i , то мера согласованности по этому признаку будет 1- μ_i . Для расчета величины μ_i могут быть применены общеизвестные статистические приемы оценки вариации в рядах распределения:

а) измерение области, содержащей основную часть ответов;

б) измерение отклонений переменных от центрально­го значения (средней, медианы);

в) измерение степени однородности качественных пе­ременных.

Исходя из природы балльных оценок наиболее прием­лемы первый и третий приемы.

При первом из них, наиболее простом и приближен­ном, в качестве меры согласованности ответов может быть, например, использован коэффициент, равный отно­шению числа ответов, совпадающих с медианой и двумя соседними с ней местами, к общему числу ответов.

Третий прием расчета меры согласованности основан на вычислении коэффициентов вариации качественных переменных. Для этого фактическое число различимых (по определенному значению признака) пар событий сравнивается с максимально возможным числом пар. По­добная мера вариации качественных признаков пред­ставляет аналог дисперсии.

На основе таблицы 2 величина коэффициента вариации для j-го признака вычисляется по формуле:

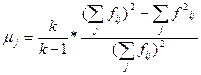, (9)

где m_j - коэффициент вариации для j-го признака;

k — число градаций (число мест) j-го признака;

fij — число ответов о присвоении i-ro места j-му признаку.

Ве­личина μ_i, меняется в пределах 0≤ μ_i ≤1.

Коэффициент μ_i приспособлен к анализу вариации качественных признаков. При расчете его величины не учитывается информация о последовательности мест; расхождение в ответах на одно место имеет такой же вес, как и расхождение в несколько мест. С целью устранения этого недостатка для ранговых признаков, А. В. Беккером предложена другая мера вариации ответов:

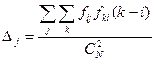, (10)

Преимуществом коэффициента вариации этого вида является учет расстояния между отдельными ответами, недостатком - оперирование разностями рангов.

Расчет подобного рода коэффициентов весьма полезен на последующих стадиях анализа - при формировании признаковых пространств и выделении однородных групп экспертов. При разбиении экспертов в первую очередь следует учитывать признаки с большой вариацией ответов по ним.

Для оценки меры сходства мнений каждой пары экспертов могут быть использованы различные методы.

Наиболее грубый подход основан на расчете так называемых коэффициентов ассоциации, с помощью которых учитывается лишь число совпадающих или несовпадающих ответов и не учитывается их последовательность. В статистической литературе описано большое число видов таких коэффициентов. Приведем один из них — информационную меру близости ответов двух экспертов:

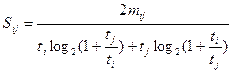, (11)

где S_ij - информационная мера близости двух ответов;

т_ij — количество признаков, одинаково оцененных i-м. и j-м специалистами;

t_i — количество признаков, оце­ненных i-м специалистом;

tj — количество признаков, оцененных /-м специалистом.

Величина S_ij меняется в пределах от 1 до 0, причем S_ij =1 указывает на полное совпадение мнений опраши­ваемых, a S_ij=0 — на полное различие мнений.

Покажем некоторые из статистических способов ана­лиза согласованности оценок, полученных от группы экспертов, на примере прогнозирования технических ха­рактеристик си