СЛУЧАЙНЫХ (РЕАЛЬНЫХ) ВЕЛИЧИН

(научная справка)

В природе и обществе все случайные реальные события рас­пределены по особым законам, выражающим свойства этих со­бытий, связанных со способами и условиями взаимодействия ка­ких-либо объектов и характеристиками их состояний. В целом, математически, принято говорить не о событиях, а о «величинах», что, конечно, значительно обедняет смысл взаимодействия или во­все игнорирует последнее. Это следует иметь в виду, когда воз­никает необходимость правильного объяснения применения зако­нов распределения в психологических исследованиях.

Говоря математическим языком, в природе и обществе обнару­живается неограниченное множество законов распределения, ана­литически, в специальных формулах представляющих знания о спе­цифике реальных событий («случайных величин»). Множество за­конов соответствует множеству реальных событий, являющихся «случайными», — и это справедливо, поскольку законы и вообще необходимость появления каких-либо событий «пробивают» себе дорогу через случайности, то есть благодаря, а не вопреки им: если бы никаких случайных событий не происходило, — значит, не происходило бы вообще никаких событий.

Среди неограниченного множества возможных законов распре­делении случайных величин особенно выделяется закон Лапласа и Гаусса, независимо друг от друга, установивших этот закон. Действие его является распространенным для многих реальных событий в пространстве и времени ближайшего космоса, к кото­рому принадлежит солнечная система и планета Земля. Распределение событий по закону Лапласа-Гаусса исторически очень ча­сто принималось за норму, поэтому данный закон называется ина­че «законом нормального распределения». Очевидно, что именно по этому закону преимущественно распределены события, наибо­лее полно отражающие сущность человека, являющуюся нам в ос­новных его психических образованиях. Характер кривой нормаль­ного распределения позволяет выделить 2 или 4, или 6 попарно одинаковых долей общей площади, охватывающей 99,72% случаев частоты проявления психических образований человека при боль­ших количествах наблюдений:

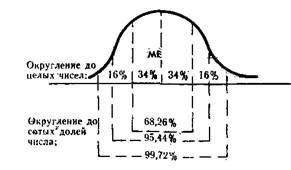
Рис. 1. Процентное распределение случаев проявления

основных психических образований человека, представляемое

кривой нормального распределения

На рисунке 1 особо следует обратить внимание на то, что все­го 4 попарно одинаковых доли площади под кривой нормального распределения охватывают 95,44% случаев проявления психиче­ских образований человека. В частности, в психодиагностике впол­не достаточно ограничиться допущением всего лишь четырех ос­новных вариаций проявления свойств личности по тому или иному ее параметру. При округлении до целых чисел эти вариации по­следовательно размещаются в отношении медианы «МЕ» следую­щим образом: 16% —34% —МЕ —34% — 16%, с учетом допуще­ния ошибки примерно в двух процентах случаев из 100%, что не противоречит обычным требованиям психологической практики. То есть, в практической психологии может быть вполне приемлем квазиквартильный подход, когда значения вариаций делят вместе с медианой все множество значений на четыре подмножества. Эти значения удобнее по-прежнему называть квартилями по тождест­венности их смыслов, несмотря на их количественное неравенство, когда первый и четвертый квартили соответствуют 16%, а второй и третий — 34% всех случаев проявлений изучаемых психических образований человека.

Глава 2