Структурно-сложная динамическая система

Структура современных моделей часто соответствует структуре изучаемого объекта. В основе таких моделей лежит элемент (блок), со скрытой от внешнего наблюдателя внутренней структурой. Таким образом, блок является «черным ящиком», который математически связывает специальные переменные, называемые в общем случае контактными (входы и выходы блока) (Рис. 1.1).

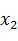
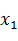
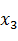
Рис. 1.1. Блок «Сравнивающее устройство»

Структурно-сложная модель состоит из множества блоков, взаимодействующих между собой через функциональные связи между видимыми извне переменными (Рис. 1.2).

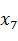
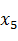
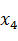
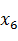
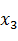
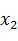
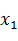
Рис. 2.1 Структурно-сложная модель

Множество элементов системы может, вообще говоря, изменяться в процессе функционирования системы. Как правило, элементы сложной системы характеризуются различными физическими принципами действия, что, в конце концов, не столь заметно в итоговой математической модели, но чрезвычайно важно на этапе построения модели.

Часто при описании сложных моделей используют составные блоки, которые могут включать в себя элементарные (неделимые) блоки, а также другие составные блоки. Данные блоки также функционируют по принципу «черного ящика», скрывая от блоков своего уровня свою организацию и внутренние функциональные зависимости. Структура таких систем является иерархической.

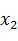
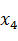
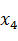
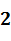
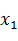
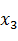
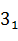
Рис. 2.1 Структурно-сложная иерархическая модель

Предположим, что на нижнем уровне иерархии всем элементарным блокам соответствуют простые динамические системы. Тогда Задачей системы моделирования является автоматическое построение для составного блока такого эквивалентного элементарного блока, чтобы его поведение соответствовало определению простой динамической системы. Поведение эквивалентного блока должно строиться по описаниям локальных систем с учетом функциональных связей. Возможность и методы автоматического построения такого эквивалентного блока, во многом зависит от того, что понимается под функциональными связями.

Наличие связи между контактами означает, что значения переменных, соответствующих контактам, в любой момент равны. В современных визуальных пакетах моделирования встречаются связи двух видов:

1) однонаправленные (ориентированные), и тогда, соединяемые контакты, делятся на приемник и источник, а также постулируется, что приемник не может влиять на источник;

2) двунаправленные (неориентированные), в этом случае соединяемые контакты равноправны.

В случае использования только однонаправленных связей контакты блоков делятся на входы и выходы (такие блоки также называются ориентированными). Входная переменная не может находиться в левой части формулы или дифференциального уравнения, а также являться искомой переменной в алгебраических уравнениях. Источником на данном уровне иерархии может быть выход внутреннего или вход внешнего блока, а приемником - вход внутреннего или выход внешнего блока. Любой источник может участвовать в любом числе связей, в то время как приемник может участвовать только в одной связи. Объединение ориентированных блоков выполняется достаточно просто: локальные уравнения и формулы механически объединяются, и каждая связь заменяется дополнительной формулой "<приемник> = <источник>". Объединение локально корректных совокупностей уравнений и формул дает корректную совокупность.

Ориентированные связи позволяют вполне адекватно описывать информационные взаимодействия между блоками в технических системах, где обычно специально принимаются меры, исключающие обратное влияние по связи.

В случае использования неориентированных связей блоки соответственно называются неориентированными. При построении совокупной системы каждая связь заменяется алгебраическим уравнением "0=<приемник>-<источник>". Напомним, что в отличие от формул, заменяемых операторами присваивания, появляющиеся алгебраические уравнения должны решаться численно. Поэтому использование неориентированных связей всегда требует больших вычислительных ресурсов, а также может вызывать проблемы с согласованием начальных условий. Далее следует провести анализ полученных совокупных уравнений и формул и выяснить, может ли она быть решена непосредственно, или требует дальнейших преобразований. К сожалению, в данном случае, в отличие от ориентированных блоков, автоматически преобразовать совокупную систему к виду, пригодному для численного решения, не всегда удается. В общем случае необходимо выполнить достаточно сложный анализ и символьные преобразования для получения эквивалентной, численно разрешимой системы.

Неориентированные связи позволяют производить декомпозицию исходного объекта на "физические" компоненты с достаточно простыми законами поведения, а затем собирать их в единую систему. В этом неоспоримое преимущество данного подхода. Недостатком является сложная и не всегда за приемлемое время осуществимая процедура автоматического построения итоговой математической модели.