Поведенческая сложность динамической системы

Одной из черт сложного поведения является наличие у системы нескольких качественно различных, последовательно сменяющих друг друга во времени, поведений (режимов функционирования). Такое сложное поведение можно реализовать, если описать всю совокупность допустимых, простых, в некотором смысле, частных поведений (возможно, это будет иерархическая структура), и указать правила переключения с одного поведения на другое. Организованная таким образом, сложная динамическая система в каждый конкретный момент времени ведет себя как некоторая простая динамическая система.

Каждое конкретное поведение можно отождествить со значением некоторой дискретной переменной, а мгновенные переключения текущего поведения - с дискретными событиями. Для передачи информации о дискретных событиях в другие блоки используют специальные переменные - сигналы. Набор дискретных состояний вместе с условиями переходов из одного состояния в другое образует обычное дискретное поведение. В моменты переходов могут происходить мгновенные скачкообразные изменения значений переменных. Поскольку в каждом из дискретных состояний элементарный блок ведет себя как некоторая непрерывная система, то поведение блока в целом является непрерывно-дискретным или гибридным.

Граф переходов, узлам которого приписаны некоторые непрерывные отображения, а дугам – условия переходов и выполняемые действия, называется гибридным автоматом.

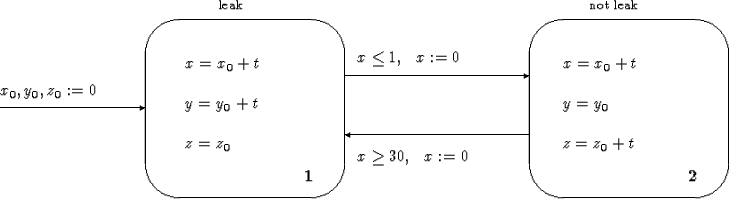
Рис. 2.2 Гибридный автомат системы контроля газовой безопасности

В настоящее время для формального описания дискретных "машин состояний" стандартом стала "карта состояний" (statechart), придуманная Д.Харелом [11] и "канонизированная" в стандарте UML[12].

Карта состояний, узлам которой приписаны некоторые непрерывные отображения, называется гибридной картой состояний.

Гибридная карта состояний представляет собой простую и очень наглядную форму визуального представления смены поведений.

Следует отметить, что существуют также системы, которые можно назвать "скрытыми гибридными". Внешне они могут выглядеть как непрерывные, но использовать в правых частях уравнений переменные, имеющие разрывы значений. Причинами этих разрывов (о которых, кстати, пользователь может и не подозревать) могут быть разного рода "нехорошие" функции, соединение непрерывных и чисто дискретных блоков, интерактивное воздействие пользователя.